SDE - Intern

How to Design BookMyShow, Fandango (or similar movie ticketing application)
A movie ticket booking application such as BookMyShow facilitates users to browse through movies and live events, watch trailers, check seat availability and purchase a ticket. Let’s discuss how to design a similar online ticketing system

For a given two strings, 'str1' and 'str2', check whether they are a permutation of each other or not.

Permutations of each other

Two strings are said to be a permutation of each other when either of the string's characters can be rearranged so that it becomes identical to the other one.

Example: 
str1= "sinrtg" 
str2 = "string"

The character of the first string(str1) can be rearranged to form str2 and hence we can say that the given strings are a permutation of each other.

You are given an array 'arr' of length 'n'. Find the index(0-based) of a peak element in the array. If there are multiple peak numbers, return the index of any peak number.

Peak element is defined as that element that is greater than both of its neighbors. If 'arr[i]' is the peak element, 'arr[i - 1]' < 'arr[i]' and 'arr[i + 1]' < 'arr[i]'.

Assume 'arr[-1]' and 'arr[n]' as negative infinity.

Note:

1.  There are no 2 adjacent elements having same value (as mentioned in the constraints).
2.  Do not print anything, just return the index of the peak element (0 - indexed).
3. 'True'/'False' will be printed depending on whether your answer is correct or not.

Example:

Input: 'arr' = [1, 8, 1, 5, 3]

Output: 3

Explanation: There are two possible answers. Both 8 and 5 are peak elements, so the correct answers are their positions, 1 and 3.

You are given a Binary Tree.

Return the length of the diameter of the tree.

Note :

The diameter of a binary tree is the length of the longest path between any two end nodes in a tree.

The number of edges between two nodes represents the length of the path between them.

Example :

Input: Consider the given binary tree:

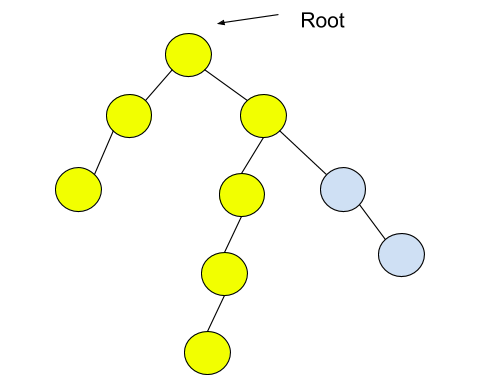
Output: 6

Explanation:
Nodes in the diameter are highlighted. The length of the diameter, i.e., the path length, is 6.

Make a fair coin from a biased coin

You are given a function foo() that represents a biased coin. When foo() is called, it returns 0 with 60% probability, and 1 with 40% probability. Write a new function that returns 0 and 1 with a 50% probability each. Your function should use only foo(), no other library method.