Athenahealth interview experience Real time questions & tips from candidates to crack your interview
Software Developer
Athenahealth
3 rounds | 8 Coding
problems
Interview preparation journey
Preparation
Duration: 6 months
Topics: Data Structures, Algorithms, System Design, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Medium
Coding Test - Pen and paper
Duration60 minutes
Interview date4 Jun 2015
Coding problem3
This test consisted of 10 questions with no negative marking to test my problem solving ability.
1. Aptitude Question
In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women?
Problem approach
Since, combinations are referred to using the following formula:
nCr = n!/(n-r)!r!
Since we need to choose, 5 men out of 9 men,
For Men = 9C5
Since, we need to choose, 3 women out of 12 women,
For Women = 12C3
Now,
Choose 5 men out of 9 men
Therefore,
nCr = n!/(n – r)!r!
9C5 = 9!/(9 – 5)!5!
9C5 = 126
Thus,
We can choose 5 men out of 9 men in 126 ways
Now, further calculating for women, Choose 3 women out of 12 women
Therefore,
nCr = n!/(n – r)!r!
12C3 = 12!/(12 – 3)!3!
12C3 = 220
Thus, Choose 3 women out of 12 women in 220 ways
Therefore, The committee can be chosen in 126 × 220 = 27720 ways.
2. Aptitude Question
Find the area of the shaded design in Fig where ABCD is a square 10 cm and semicircles are drawn with each side of the square as diameter. (Use π=3.14)
Problem approach
Given:
Side of square ABCD=10cm
Area of square ABCD=(side) ^2 =10^2 =100sq.cm
Given semicircle is drawn with side of square as diameter.
So, Diameter of semicircle=Side of square=10cm
Radius of semicircle= side/2 = 5 cm
Area of semi-circle AD= (Area of circle)/2 = (pi*r^2)/2 = (3.14×25)/2
Since radius is same for semi-circle AD,BC,AB,CD
Area of semi circleAD=Area of semi circle BC=Area of semicircle AB = Area of semicircle CD = (3.14×25)/2
Area of 4 semicircles−Area of shaded region=Area of square ABCD
Area of shaded region=Area of 4 semicircles−Area of square ABCD
=4× (3.14*25)/2 - 100=157−100=57cm^2
3. Aptitude Question
There is a chessboard of size 8×8. I am given dominoes of size 1×2 and of a single color (assume, it has a color). It is possible to place a domino on the board so that it covers exactly two squares. I can't place two dominoes on the same square and I can't place a domino so that it is partially off the board. How many ways are there to place a single domino on the board( I place it only horizontally or vertically) ?
Problem approach
Treat the centers of 64 chess positions as vertices and join neighboring vertices by edges. There are 112=2×7×8 of them. There is a one-one correspondence between possible placement of domino and the edge it covered. This means there are 112 ways to place a single domino.
02
Round
Medium
Face to Face
Duration60 minutes
Interview date4 Jun 2015
Coding problem2
Technical Interview round with questions based on DSA and algorithms.
1. Word Distance
Easy
15m average time
85% success
0/40
Asked in companies



You are given a document as an Array/List 'ARR' of words of length ‘N’. You have to perform Q queries. In each query, you are given two words. Your task is to find the smallest distance between these two words in a document and return it.
Distance between words is defined as the difference between their indexes.
For example:
ARR=[‘hot’, ‘a’, ‘b’, ‘dog’] and query = (‘hot’, ‘dog’)
The answer, in this case, is 3 as the minimum distance between ‘hot’ and ‘dog’ in the given document is 3.
Note:
If any one of the words is not present in the document then your program must return ‘N’ which is the length of the document.
Problem approach
The idea is to traverse over all the elements in the array in two nested loops. Whenever we get occurrence of word1 or word2, take the minimum of answer and the current distance.
Time Complexity : O((N^2)*M), where N is the number of elements in the array and M is the maximum length of a string present in the array.
The idea is to get all the indices where ‘word1’ and ‘word2’ are present and store the indices in an array. Both the arrays will already be sorted as we found the indices by iterating over the array. Then we will use the two-pointer approach to find the minimum distance between ‘word1’ and ‘word2’.
Algorithm:
• Declare two arrays, that store the indices in which word1 and word2 are present, respectively.
• Declare a variable answer to store the maximum integer value.
• Iterate over the array ‘arr’:
o If the name of the current element is the same as ‘word1’, push the current index into the first array.
o If the name of the current element is the same as ‘word2’, push the current index into the second array.
• Initialize two pointers, ‘i’ and ‘j’, which point to the beginning of both the arrays, respectively.
• Execute a while loop with the condition i is less than the size of the first array and j is less than the size of the second array :
o Update ‘answer’ as the minimum of ‘answer’ and an absolute value of (i-j).
o If j > i, increment i by 1.
o Otherwise, increment j by 1.
• When it comes out of the loop, then return ‘answer’ as the final answer.
2. Sudoku?
Moderate
40m average time
60% success
0/80
Asked in companies



You have been given a 9 X 9 2D matrix 'MATRIX' with some cells filled with digits(1 - 9), and some empty cells (denoted by 0).
You need to find whether there exists a way to fill all the empty cells with some digit(1 - 9) such that the final matrix is a valid Sudoku solution.
A Sudoku solution must satisfy all the following conditions-
1. Each of the digits 1 - 9 must occur exactly once in each row.
2. Each of the digits 1 - 9 must occur exactly once in each column.
3. Each of the digits 1 - 9 must occur exactly once in each of the 9, 3 x 3 sub-matrices of the matrix.
Note
1. There will always be a cell in the matrix which is empty.
2. The given initial matrix will always be consistent according to the rules mentioned in the problem statement.
Problem approach
The idea is to check whether each row, column, and 3×3 box is valid or not on the basis of the following points:
1. The Sudoku board could be partially filled, where empty cells are filled with the character ‘.’.
2. An empty Sudoku board is also valid.
3. A valid Sudoku board (partially filled) is not necessarily solvable. Only the filled cells need to be validated.
03
Round
Easy
Face to Face
Duration60 minutes
Interview date4 Jun 2015
Coding problem3
You will be having 2 or 3 members per panel and questions may be from databases , object oriented programming, operating systems, Linux commands and algorithm may be asked for problems
1. Cycle Detection in a Singly Linked List
Moderate
15m average time
80% success
0/80
Asked in companies



You are given a Singly Linked List of integers. Return true if it has a cycle, else return false.
A cycle occurs when a node's next points back to a previous node in the list.
Example:
In the given linked list, there is a cycle, hence we return true.
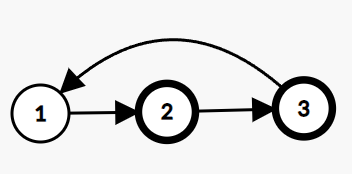
Problem approach
Floyd's algorithm can be used to solve this question.
Define two pointers slow and fast. Both point to the head node, fast is twice as fast as slow. There will be no cycle if it reaches the end. Otherwise, it will eventually catch up to the slow pointer somewhere in the cycle.
Let X be the distance from the first node to the node where the cycle begins, and let X+Y be the distance the slow pointer travels. To catch up, the fast pointer must travel 2X + 2Y. L is the cycle size. The total distance that the fast pointer has travelled over the slow pointer at the meeting point is what we call the full cycle.
X+Y+L = 2X+2Y
L=X+Y
Based on our calculation, slow pointer had already traveled one full cycle when it met fast pointer, and since it had originally travelled A before the cycle began, it had to travel A to reach the cycle's beginning!
After the two pointers meet, fast pointer can be made to point to head. And both slow and fast pointers are moved till they meet at a node. The node at which both the pointers meet is the beginning of the loop.
Pseudocode :
detectCycle(Node *head) {
Node *slow=head,*fast=head;
while(slow!=NULL && fast!=NULL && fast->next!=NULL) {
slow = slow->next;
fast = fast->next->next;
if(slow==fast)
{
fast = head;
while(slow!=fast)
{
slow = slow->next;
fast=fast->next;
}
return slow;
}
}
return NULL; }
2. Level Order Traversal
Easy
15m average time
85% success
0/40
Asked in companies



You have been given a Binary Tree of integers. You are supposed to return the level order traversal of the given tree.
For example:
For the given binary tree
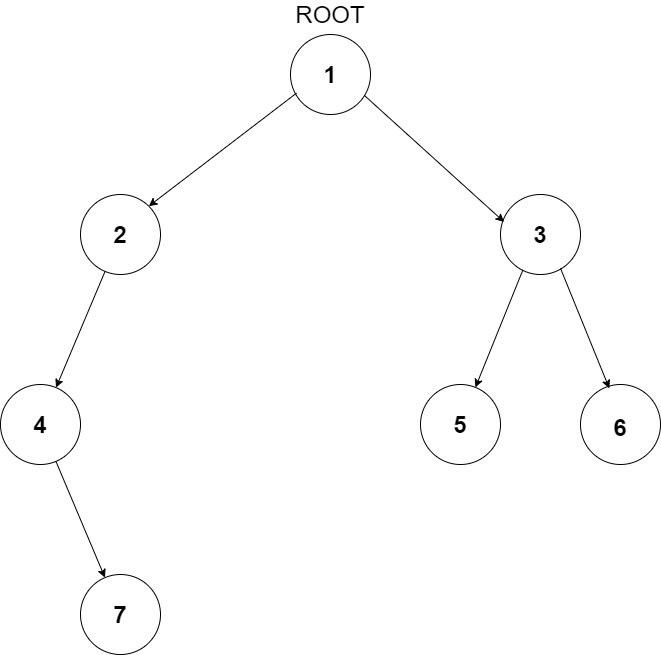
The level order traversal will be {1,2,3,4,5,6,7}.
Problem approach
the node and then push its children nodes in the FIFO queue.
printLevelorder(tree)
1) Create an empty queue q
2) temp_node = root /*start from root*/
3) Loop while temp_node is not NULL
a) print temp_node->data.
b) Enqueue temp_node’s children (first left then right children) to q
c) Dequeue a node from q.
Time Complexity: O(n) where n is the number of nodes in the binary tree
Space Complexity: O(n) where n is the number of nodes in the binary tree
3. OOPS Question
What are virtual functions ?
Problem approach
A C++ virtual function is a member function in the base class that you redefine in a derived class. It is declared using the virtual keyword. It is used to tell the compiler to perform dynamic linkage or late binding on the function. A 'virtual' is a keyword preceding the normal declaration of a function. When the function is made virtual, C++ determines which function is to be invoked at the runtime based on the type of the object pointed by the base class pointer.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
4 rounds | 5 problems
Interviewed by Athenahealth
3512 views
0 comments
0 upvotes
Associate Software Engineer
4 rounds | 5 problems
Interviewed by Athenahealth
1673 views
0 comments
0 upvotes
Software Developer
4 rounds | 12 problems
Interviewed by Athenahealth
1831 views
0 comments
0 upvotes
Member of Technical Staff
3 rounds | 3 problems
Interviewed by Athenahealth
1981 views
0 comments
0 upvotes
Companies with similar interview experiences
Software Developer
5 rounds | 14 problems
Interviewed by Microsoft
3986 views
1 comments
0 upvotes
Software Developer
6 rounds | 12 problems
Interviewed by SAP Labs
2872 views
0 comments
0 upvotes
Software Developer
3 rounds | 3 problems
Interviewed by Amazon
1201 views
0 comments
0 upvotes








