Directi interview experience Real time questions & tips from candidates to crack your interview
Software Developer
Directi
3 rounds | 5 Coding
problems
Interview preparation journey
Preparation
Duration: 5 months
Topics: Data Structures, Algorithms, System Design, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Medium
Face to Face
Duration45 minutes
Interview date11 May 2016
Coding problem1
This was a technical round with questions on DSA.
1. Count all sub-arrays having sum divisible by k
Moderate
15m average time
85% success
0/80
Asked in companies



Given an array ‘ARR’ and an integer ‘K’, your task is to find all the count of all sub-arrays whose sum is divisible by the given integer ‘K’.
Note:
If there exists no subarray in the given sequence whose sum is divisible by ‘K’ then simply return ‘0’.
Example:
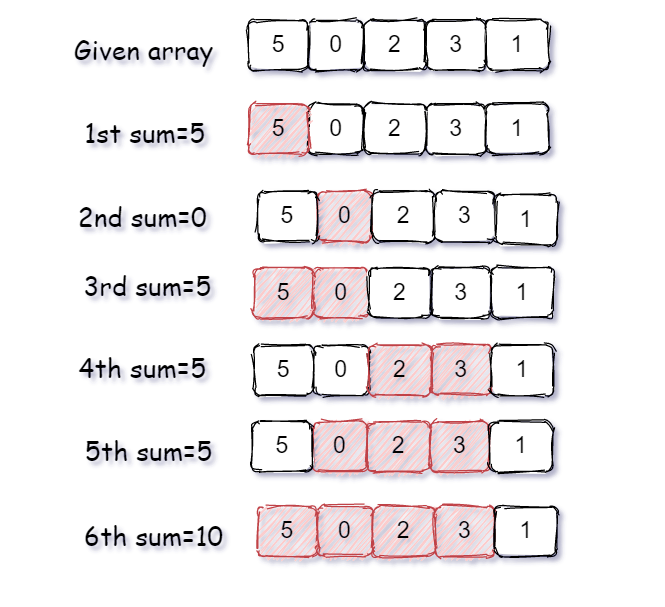
Suppose the given array is ‘ARR’ = { 5, 0, 2, 3, 1} and ‘K = 5’.
As we can see in below image, there are a total of 6 subarrays that have the total sum divisible by ‘K’
So we return the integer 6.
Problem approach
1) To implement this approach we need a hashmap to call it ‘REM_MAP’, which stores reminders and frequency of remainder and adds ‘0’ remainder with frequency ‘1’ because we can consider empty subarray has sum and remainder is ‘0’.
2) A variable ‘COUNT’ in which we store the count of all the subarray has sum divisible by ‘K’ and initially, value is ‘0’.
3) Iterate ‘i’ from ‘0’ to ‘N-1’.
4) Calculate the sum of all the elements from index ‘0’ to 'i’ in a variable ‘SUM’.
5) And find current remainder with ‘SUM % K’
- If the current remainder is present in ‘REM_MAP the added frequency of the current remainder in ‘COUNT’ variable and update frequency of current remainder by adding one
- Let’s take an example, suppose the current remainder is ‘3’ and ‘REM_MAP’ has a key-value pair of ‘3: 4’ which means remainder 3 hash 4 frequency then add ‘4’ in ‘COUNT’ and update ‘3: 4’ with ‘3: 5’ by adding one more frequency.
6) If ‘REM_MAP’ has no current remainder then add current remainder with frequency = 1.
7) Iterate for next ‘i’.
8) In the end, return ‘COUNT’.
TC : O(N), where N = size of the array
SC : O(k)
02
Round
Medium
Face to Face
Duration45 minutes
Interview date11 May 2016
Coding problem2
This was the second algorithmic round.
1. Search in a row wise and column wise sorted matrix
Moderate
15m average time
80% success
0/80
Asked in companies



You are given an 'N * N' matrix of integers where each row and each column is sorted in increasing order. You are given a target integer 'X'.
Find the position of 'X' in the matrix. If it exists then return the pair {i, j} where 'i' represents the row and 'j' represents the column of the array, otherwise return {-1,-1}
For example:
If the given matrix is:
[ [1, 2, 5],
[3, 4, 9],
[6, 7, 10]]
We have to find the position of 4. We will return {1,1} since A[1][1] = 4.
Problem approach
The brute force solution is to traverse the array and to search elements one by one. Run a nested loop, outer loop for row and inner loop for the column
Check every element with x and if the element is found then print “element found”. If the element is not found, then print “element not found”.
Efficient Approach : The idea here is to remove a row or column in each comparison until an element is found. Start searching from the top-right corner of the matrix. There are three possible cases :
1. The given number > the current number: This will ensure that all the elements in the current row are smaller than the given number as the pointer is already at the right-most elements and the row is sorted. Thus, the entire row gets eliminated and continues the search for the next row.
2. The given number < the current number: This will ensure that all the elements in the current column are greater than the given number. Thus, the entire column gets eliminated and continues the search for the previous column, i.e. the column on the immediate left.
3. The given number == the current number: This will end the search.
• Algorithm:
1. Let the given element be x, create two variable i = 0, j = n-1 as index of row and column
2. Run a loop until i = n
3. Check if the current element is greater than x then decrease the count of j. Exclude the current column.
4. Check if the current element is less than x then increase the count of i. Exclude the current row.
5. If the element is equal, then print the position and end.
2. Count all possible paths from top left to bottom right of a mXn matrix
Moderate
25m average time
80% success
0/80
Asked in companies


You are present at point ‘A’ which is the top-left cell of an M X N matrix, your destination is point ‘B’, which is the bottom-right cell of the same matrix. Your task is to find the total number of unique paths from point ‘A’ to point ‘B’.In other words, you will be given the dimensions of the matrix as integers ‘M’ and ‘N’, your task is to find the total number of unique paths from the cell MATRIX[0][0] to MATRIX['M' - 1]['N' - 1].
To traverse in the matrix, you can either move Right or Down at each step. For example in a given point MATRIX[i] [j], you can move to either MATRIX[i + 1][j] or MATRIX[i][j + 1].
Problem approach
We have a matrix with n rows and m columns, where each cell, matrix[A][B], denotes whether it is accessible or not.
We will use recursion to solve this problem. We know that the number of ways to reach a cell is the sum of the number of ways to reach the cell to its left and the number of ways to reach the cell above it. Therefore:
No. of ways to reach matrix[i][j] = No. of ways to reach matrix[i-1][j] + No. of ways to reach matrix[i][j-1]
This is because we can only go right or downward from any cell.
Now, we start from a cell and perform recursion to find the number of ways to reach cell (n-1, m-1):
recur(matrix, n-1, m-1) = recur(matrix, n-2, m-1) + recur(matrix, n-1, m-2)
For each cell, we will check if it is accessible or not. If it is not, we simply return 0, as there is no way to reach it. The base condition would be that if cell (0,0) is accessible, then the number of ways to reach it is 1.
Time Complexity: O(2^(rows+columns))
Auxiliary Space Used: O(rows+columns)
The above solution (recursive) was exponential. We are visiting multiple states over and over, and then recursing for them, which we can surely avoid. To avoid revisiting states that have already been visited, we can store them in a dp array, so that they can be accessed as and when needed. This approach is known as Dynamic Programming.
We know that for any cell (i, j), the number of paths to reach it would be the number of paths to reach cell (i-1, j) + the number of paths to reach cell (i, j-1).
For any accessible cell matrix[i][j], we maintain the count of number of paths to reach this cell in a separate two-dimensional array dp[i][j], where dp[i][j] = dp[i-1][j] + dp[i][j-1], given that cell (i, j) is accessible.
We return the value of dp[i][j] as the answer.
Time Complexity: O(n*m), considering the number of rows is n and columns is m.
Space Complexity: O(n*m), considering the number of rows is n and columns is m.
03
Round
Medium
Face to Face
Duration60 minutes
Interview date11 May 2016
Coding problem2
This was the third algorithmic round.
1. Check whether a given graph is Bipartite or not
Moderate
0/80
Asked in companies



You are given an undirected graph consisting of ‘N’ nodes from 0 to ‘N’ - 1. You are given a list ‘EDGES’ of size ‘M’, consisting of all the edges of this undirected graph. Determine whether the given graph is Bipartite or not.
Note:
The graph has no self-edges, no parallel edges.
The graph may not be connected.
A graph is bipartite if the nodes of the graph can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
For Example,
If ‘N’ = 4, ‘M’ = 5, edgeList = [ [0, 1],[0, 3],[1, 2] ].

Here, you can see that the graph is bipartite as we can divide the nodes in two sets as follows:
setA = [0, 2].
setB = [1, 3].
In the graph, you can see that every edge in the graph connects a node in set A and a node in set B.
Hence, the output is “Yes”.
Problem approach
One approach is to check whether the graph is 2-colorable or not using backtracking algorithm m coloring problem.
Following is a simple algorithm to find out whether a given graph is Bipartite or not using Breadth First Search (BFS).
1. Assign RED color to the source vertex (putting into set U).
2. Color all the neighbors with BLUE color (putting into set V).
3. Color all neighbor’s neighbor with RED color (putting into set U).
4. This way, assign color to all vertices such that it satisfies all the constraints of m way coloring problem where m = 2.
5. While assigning colors, if we find a neighbor which is colored with same color as current vertex, then the graph cannot be colored with 2 vertices (or graph is not Bipartite)
2. Longest Alternating Subsequence
Moderate
15m average time
85% success
0/80
Asked in companies



You are given an array ‘ARR’ of integers. Your task is to find the length of the longest alternating subsequence.
Note:
A sequence a1, a2, .... an is called an alternating sequence if its elements satisfy one of the following relations : a1 < a2 > a3 < a4 > a5..... or a1 > a2 < a3 > a4 < a5.
For example:
'ARR' = {3, 10, 1, 2, 30}, the longest alternating subsequence for this array can be {3, 10, 1, 30} or {3, 10, 2, 30}. Therefore, the answer will be 4.
Problem approach
1) Use a 2-D array ‘DP[N][2]’ to store the values, in which ‘DP[i][0]’ stores the answer till the current index ‘i’ when ‘ARR[i]’ > ‘ARR[i - 1]’ and ‘DP[i][1]’ stores the answer for the index when ‘ARR[i]’ < ‘ARR[i - 1]’.
2) Declare ‘RESULT’ = ‘0’.
3) Initialize ‘DP[0][0]’ and ‘DP[0][1]’ as zero as these are the base cases.
4) Run two nested loops outer one starting from ‘i’ = ‘0’ to ‘N’ and the inner one starting from ‘j’ = 0 till ‘i’.
5) Check if('ARR[i]' > ‘ARR[j]’), store ‘DP[i][0]’ = max('DP[i][0]', ‘DP[j][1]’ + 1);
6) Similarly if('ARR[i]' < ‘ARR[j]’), store ‘DP[i][0]’ = max('DP[i][1]', ‘DP[j][0]’ + 1);
7) Update the ‘RESULT’ in every iteration.
8) Finally, return the ‘RESULT’.
TC : O(N^2), where N = size of the array
SC : O(N)

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - Intern
2 rounds | 5 problems
Interviewed by Directi
1521 views
0 comments
0 upvotes
SDE - 1
3 rounds | 10 problems
Interviewed by Directi
884 views
0 comments
0 upvotes
SDE - 1
2 rounds | 4 problems
Interviewed by Directi
0 views
0 comments
0 upvotes
SDE - 1
4 rounds | 7 problems
Interviewed by Directi
883 views
0 comments
0 upvotes
Companies with similar interview experiences
Software Developer
5 rounds | 14 problems
Interviewed by Microsoft
3986 views
1 comments
0 upvotes
Software Developer
6 rounds | 12 problems
Interviewed by SAP Labs
2872 views
0 comments
0 upvotes
Software Developer
3 rounds | 3 problems
Interviewed by Amazon
1202 views
0 comments
0 upvotes





