Facebook interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Facebook
4 rounds | 10 Coding
problems
Interview preparation journey
Preparation
Duration: 4 Months
Topics: Data Structures, Algorithms, System Design, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Hard
Online Coding Test
Duration90 minutes
Interview date10 Jul 2021
Coding problem2
This was an online coding round where we had 2 questions to solve under 90 minutes . Both the questions were preety hard according to me . One has to have a fair share of knowledge in Data Structures and Algorithms to pass this round .
1. Longest Increasing Path In A 2D Matrix
Hard
10m average time
90% success
0/120
Asked in companies



You have been given a MATRIX of non-negative integers of size N x M where 'N' and 'M' denote the number of rows and columns, respectively.
Your task is to find the length of the longest increasing path when you can move to either four directions: left, right, up or down from each cell. Moving diagonally or outside the boundary is not allowed.
Note: A sequence of integers is said to form an increasing path in the matrix if the integers when traversed along the allowed directions can be arranged in strictly increasing order. The length of an increasing path is the number of integers in that path.
For example :
3 2 2
5 6 6
9 5 11
In the given matrix, 3 → 5 → 6 and 3 → 5 → 9 form increasing paths of length 3 each.
Problem approach
This was one of the most interesting questions I faced in all my campus interviews . I was initially thinking of using recursion and then optimising it through memoisation but there was a risk of getting TLE . I then observed that this question can be transformed into a Topological Sort+DP question where I was required to find the length of the longest chain ending at a particular index .
Steps :
1) Construct a graph (adjacency list) from the given matrix .
2) For every (i,j) check its 4 directions up,down,left,right .
3) If arr[i+1][j] > arr[i][j] , add a directed graph from (i,j) to (i+1,j).
4) Similarly, perform these steps for the other 3 directions.
5) Also , increment the indegree of the node to which we direct the edge
6) Now, initialise a queue of pair of int . Add all those nodes whose indegree was 0
7) Perform a standard BFS Topo Sort i.e., run a loop till my queue becomes empty and update the dp[node] (which stores the max length of a increasing chain ending at node) .
8) Finally, return the max value of dp[node] for all nodes.
2. Saving Money
Moderate
20m average time
80% success
0/80
Asked in companies



Ninja likes to travel a lot, but at the same time, he wants to save as much money as possible.
There are ‘N’ Stations connected by ‘M’ Trains. Each train that he boards starts from station ‘A’ and reaches destination station ‘B’ with a ticket price ‘P’.
Your task is to return the cheapest price from the given ‘source’ to ‘destination’ with up to ‘K’ stops. If there is no such route, return ‘-1’.
For example:
Input:
5 6
0 1 10
0 2 10
0 3 40
1 4 10
2 4 20
4 3 5
0 3 40

There are three ways to reach station ‘3’ from station ‘0’. The first path is 0->1->4->3, which will cost us 10+ 10+ 5= 25 and the second path 0->2->4->3 will cost us, 10+ 20+ 5 = 35, and the third path 0->3 will cost us 40.
We can’t take the first path since K = 1 and in this path, we are taking 2 stops, at station ‘1’ and station ‘4’.
Similarly, there are 2 stops in the second path. Hence we’ll finally choose the 3rd path i.e. 0->3, which is colored in blue.
Problem approach
It seems that Facebook loves Graph questions . This was also a Graph question particularly related to Bellman Ford Algorithm .
Steps :
1) Initiliase a DP array with all INT_MAX , where dp[i][j] stores the min distance to reach j from source using atmost i edges.
2) For all i from 0 to k+1 , dp[i][src]=0 as min distance to reach source (src) using any no. of edges is always 0 .
3) Run a loop from 1 to k+1 and then again an inner loop which loops through all the elements of the flights vector .
4) Now , if there is a flight from u to v that costs w then we have the following transiition for dp[i][v] i.e., the min distance to reach v using atmost i edges
If dp[u][i-1]!=INT_MAX , then dp[i][v]=min(dp[i][v] , dp[i-1][u]+w)
5) Finally, return dp[k+1][dist].
02
Round
Medium
Video Call
Duration60 Minutes
Interview date12 Jul 2021
Coding problem2
This Round was DS and Algo round and it started with formal introduction, followed by 2 problems. We first dicussed the
approach the time complexity and proper code covering all cases.
1. K - Sum Path In A Binary Tree
Moderate
35m average time
65% success
0/80
Asked in companies



You are given a binary tree in which each node contains an integer value and a number ‘K’. Your task is to print every path of the binary tree with the sum of nodes in the path as ‘K’.
Note:
1. The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).
2. Output the paths in the order in which they exist in the tree from left to right. Example: In the below example, path {1,3} is followed by {3,1} and so on.
Example:
For K = 4 and tree given below:
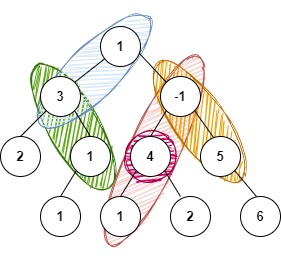
The possible paths are:
1 3
3 1
-1 4 1
4
-1 5
The sum of values of nodes of each of the above-mentioned paths gives a sum of 4.
Problem approach
The idea is simple: along the path, record all prefix sums in a hash table. For current prefix sum x, check if (x - target)
appears in the hash table.
Steps :
1) We will be using a unordered map which will be filled with various path sum.
2) For every node we will check if current sum and root’s value equal to k or not. If the sum equals to k then
increment the required answer by one.
3) Then we will add all those path sum in map which differs from current sum+root->data value by a constant integer
k.
4) Then we will be inserting the current sum + root->data value in the map.
5) We will recursively check for left and right subtrees of current root
6) After the right subtree is also traversed we will remove the current sum + root->data value from the map so that it
is not taken into consideration in further traversals of other nodes other than the current root’s.
TC : O(n) where n is the total number of nodes in the tree
SC : O(n)
2. Combination Sum
Easy
15m average time
85% success
0/40
Asked in companies



You are given an array 'ARR' of 'N' distinct positive integers. You are also given a non-negative integer 'B'.
Your task is to return all unique combinations in the array whose sum equals 'B'. A number can be chosen any number of times from the array 'ARR'.
Elements in each combination must be in non-decreasing order.
For example:
Let the array 'ARR' be [1, 2, 3] and 'B' = 5. Then all possible valid combinations are-
(1, 1, 1, 1, 1)
(1, 1, 1, 2)
(1, 1, 3)
(1, 2, 2)
(2, 3)
Problem approach
Since the constraints were small , I followed a recursive+backtracking approach for this problem
Approach :
1) Create a recursive function called recur (void recur(vector&arr , vectortmp , int target,int idx) ) which would eventually fill my answer vector with all the possible combination sums for the given target.
2) For every element , I have 2 choices -
2.1) To take that element and decrease my target by arr[idx] and again call the same recursive function
recur for the remaining target.
2.2) To not take that element and simply call the recursive function for the same target but with an
updated index idx+1.
3) For every element that we push into tmp , we should also pop it after step 2.1 as we may not end up using that element .
4) As target==0, push the tmp vector into my answer vector and simply return from the function
5) One more base case : If idx>arr.size() or target<0 or (idx==n and target>0) , simply return from the function.
TC : O(2^n) where n=size of vector arr
SC : O(target)
03
Round
Medium
Video Call
Duration50 Minutes
Interview date12 Jul 2021
Coding problem3
This Round was DS/Algo + Core round and it started with formal introduction, followed by 3 problems. We first dicussed
the approach the time complexity and proper code covering all cases for the 2 coding problems . The last question was
related to OS and was a bit theoretical .
1. Accounts Merge
Hard
15m average time
85% success
0/120
Asked in companies



You have been given an array/list 'accounts' where each element, i.e. 'accounts'[i] contains a list of strings.
In 'accounts'[i], the first element is the name of the account holder, and the rest of the strings are emails representing the emails of the account.
Now, you are supposed to merge the accounts. Two accounts definitely belong to the same person if there is some email that is common to both accounts. Note that it may be possible that two accounts belong to the same name, but they may belong to different people, as people could have the same name.
A person could have any number of accounts initially, but all their accounts definitely have the same name.
After merging the accounts, you have to return an array/list of merged accounts where each account, the first element is the person's name, and the rest elements are the email addresses in sorted order (non-decreasing). Accounts themselves can be in any order.
Example:
Input: 'n' = 4,
'accounts' = [
["Rohan", "rohan123@gmail.com", "1279ro@gmail.com"],
["Rohit", "rohit101@yahoo.com", "hitman30487@gmail.com"],
["Rohan", "1279ro@gmail.com", "niemann01@gmail.com"],
["Rohan", "kaushik@outlook.com"],
]
Output: [
["Rohan", "rohan123@gmail.com", "1279ro@gmail.com", "niemann01@gmail.com"],
["Rohit", "rohit101@yahoo.com", "hitman30487@gmail.com"],
["Rohan", "kaushik@outlook.com"],
]
Explanation: The first and third "Rohan" are the same person as they have a shared email address, “1279ro@gmail.com”. The rest of the accounts are of different persons, as they don’t share any shared email addresses. So, we merge the first and third accounts.
Problem approach
My Interviewer took some time in explaining this problem to me as the problem statement of this question was quite long and complicated . After thoroughly understanding the question , my first observation was to apply DFS and solve this problem but some time later the thought of using Disjoint Set Union or DSU crossed my mind and then I was sure to implement my idea using DSU .
Approach :
1) Traverse over each account, and for each account, traverse over all of its emails. If we see an email for the first time, then set the group of the email as the index of the current account in emailGroup .
2) Otherwise, if the email has already been seen in another account, then we will union the current group (i) and the group the current email belongs to (emailGroup[email]).
3) After traversing over every account and merging the accounts that share a common email, we will now traverse over every email once more. Each email will be added to a map (components) where the key is the email's representative, and the value is a list of emails with that representative.
4) Traverse over components, here the keys are the group indices and the value is the list of emails belonging to this group (person). Since the emails must be "in sorted order" we will sort the list of emails for each group. Lastly, we can get the account name using the accountList[group][0]. In accordance with the instructions, we will insert this name at the beginning of the email list.
5) Store the list created in step 4 in our final result (mergedAccount).
TC : O(N*K*log(N*K)) where N is the number of accounts and K is the maximum length of an account.
SC : O(N*K)
2. Construct Binary Tree From Inorder and Preorder Traversal
Easy
10m average time
90% success
0/40
Asked in companies



You have been given the preorder and inorder traversal of a binary tree. Your task is to construct a binary tree using the given inorder and preorder traversals.
Note:
You may assume that duplicates do not exist in the given traversals.
For example :
For the preorder sequence = [1, 2, 4, 7, 3] and the inorder sequence = [4, 2, 7, 1, 3], we get the following binary tree.
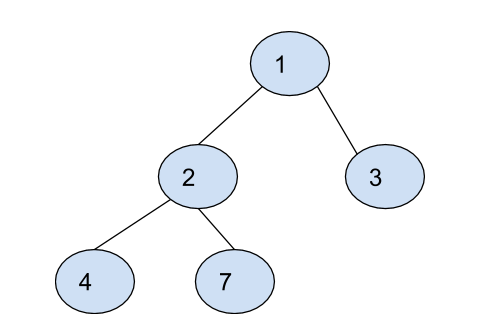
Problem approach
This was a preety standard question and I had already solved it in platforms like LeetCode and CodeStudio so coding it was not so difficult for me . I first explained my intuition and approach to the interviewer and after that started coding it in my machine . After coding , we discussed its Time and Space Complexity .
Approach :
The two key observations are:
1) Preorder traversal follows Root -> Left -> Right, therefore, given the preorder array preorder, we have easy access to the root which is preorder[0].
2) Inorder traversal follows Left -> Root -> Right, therefore if we know the position of Root, we can recursively split the entire array into two subtrees.
Steps :
1) Build a hashmap to record the relation of value -> index for inorder, so that we can find the position of root in constant time.
2) Initialize an integer variable preorderIndex to keep track of the element that will be used to construct the root.
3) Implement the recursion function arrayToTree which takes a range of inorder and returns the constructed binary tree:
3.1) if the range is empty, return null;
3.2) initialize the root with preorder[preorderIndex] and then increment preorderIndex;
3.3) recursively use the left and right portions of inorder to construct the left and right subtrees.
4) Simply call the recursion function with the entire range of inorder.
TC : O(N) where N=size of the input array
SC : O(N)
3. OS Question
Explain Demand Paging .
Problem approach
Demand paging is a method that loads pages into memory on demand. This method is mostly used in virtual memory.
In this, a page is only brought into memory when a location on that particular page is referenced during execution.
The following steps are generally followed:
1) Attempt to access the page.
2) If the page is valid (in memory) then continue processing instructions as normal.
3) If a page is invalid then a page-fault trap occurs.
4) Check if the memory reference is a valid reference to a location on secondary memory. If not, the process is terminated (illegal memory access). Otherwise, we have to page in the required page.
5) Schedule disk operation to read the desired page into main memory.
6) Restart the instruction that was interrupted by the operating system trap.
04
Round
Medium
Video Call
Duration60 minutes
Interview date12 Jul 2021
Coding problem3
This was a preety intense round as I was grilled more on my System Design concepts but eventually I was able to
asnwers all the questions with some help from the interviewer.
General Tip : While preparing for Facebook Interviews , make sure you read and understand some of the most important features that Facebook incorporates like Graph Search , Adding a friend , Removing a friend , Storing Likes/Dislikes and so on.
All these features are important to learn because at their core they are nothing but Data Structures used and implemented very elegantly . So before your next Facebook interview , do read these topics and be confident about your LLD as well as HLD skills.
1. System Design Question
How does Facebook store likes/dislikes ?
Problem approach
Approach :
1) We can keep one counter variable which counts the overall likes in that same document where the post's data is present.
2) And store the details/uids of people who liked it in different documents( this way, when we tap on details, then only we'll need to fetch these docs) and, we can setup a cloud func whch updates that counter whenever someone likes/dislikes.
3) To check that user has liked or not, we can just check if the current user's uid is present in the likes/dislikes.
2. System Design Question
How does Facebook implement graph search ?
Problem approach
Answer :
1) Facebook graph search, can be considered as a complex graph with entities like people, pages, photos and videos, while the edges are relationships among all of these entities.
2) Unicorn- standard inverted index system optimized for the needs of Facebook is used for having all the information on the main memory so the query processing doesn't involve any disk access.
3) Unicorn processes queries that select a section of the social graph.
4) Unicorn is essentially built like a standard search engine that maps terms to sets of documents; unlike a text search engine, the terms aren't words, but connections in the social graph (for example, "friend:4" maps to the ids of all users who are friends with the user with id 4; similar terms for "photos taken by user id 4", "users who like page with id 25" etc).
On top of this, there are other layers (parsing natural language queries, ranking, privacy filtering, rendering the results, etc) but Unicorn sits at the core.
3. System Design Question
How does Facebook Chat works ?
Problem approach
I was asked to answer this question w.r.t 2 very important aspects on how a chat system becomes more engaging to
its users.
Answer :
Real-time messaging :
1) The method FB chooses to get text from one user to another involves loading an iframe on each Facebook page,
and having that iframe’s Javascript make an HTTP GET request over a persistent connection that doesn’t return until
the server has data for the client.
2) The request gets re-established if it’s interrupted or times out. This is a variation of Comet, specifically XHR long
polling, and/or BOSH.
3) Having a large-number of long-running concurrent requests makes the Apache part of the standard LAMP stack a
dubious implementation choice.
Real-time presence notification :
1) The naive implementation of sending a notification to all friends whenever a user comes online or goes offline has
a worst case cost of O(average friendlist size * peak users * churn rate) messages/second, where churn rate is the
frequency with which users come online and go offline, in events/second.
2) Surfacing connected users’ idleness greatly enhances the chat user experience but further compounds the
problem of keeping presence information up-to-date.
3) Each Facebook Chat user now needs to be notified whenever one of his/her friends (a) takes an action such as
sending a chat message or loads a Facebook page (if tracking idleness via a last-active timestamp) or (b) transitions
between idleness states (if representing idleness as a state machine with states like “idle-for-1-minute”, “idle-for-2-
minutes”, “idle-for-5-minutes”, “idle-for-10-minutes”, etc.).
4) Approach (a) changes the sending a chat message / loading a Facebook page from a one-to-one communication
into a multicast to all online friends, while approach (b) ensures that users who are neither chatting nor browsing
Facebook are nonetheless generating server load.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SWE Intern
2 rounds | 5 problems
Interviewed by Facebook
1331 views
0 comments
0 upvotes
SDE - Intern
2 rounds | 3 problems
Interviewed by Facebook
1610 views
0 comments
0 upvotes
SDE - 1
5 rounds | 10 problems
Interviewed by Facebook
922 views
0 comments
0 upvotes
SDE - 1
4 rounds | 8 problems
Interviewed by Facebook
963 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114868 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58030 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35056 views
7 comments
0 upvotes






