SDE - 1 Razorpay interview experience | Anshuman Tripathi

Interview rounds

Round

Medium

Online Coding Test

Duration120 minutes

Interview date20 May 2022

Coding problem2

Two coding Question

1. Maximum Size Rectangle Sub-matrix With All 1's

Hard

10m average time

80% success

0/120

Asked in companies

You are given an 'N' * 'M' sized binary-valued matrix 'MAT, where 'N' is the number of rows and 'M' is the number of columns. You need to return the maximum size (area) of the submatrix which consists of all 1’s i.e. the maximum area of a submatrix in which each cell has only the value ‘1’.

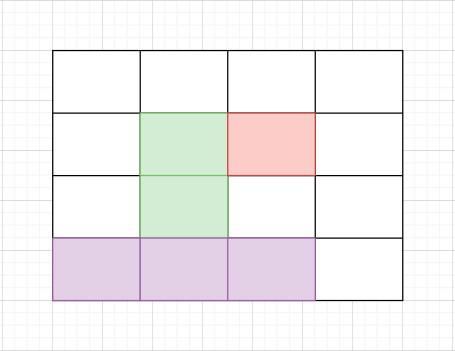
In the above image, areas in green, red, and violet color are all submatrices of the original 4x4 matrix.

Note:

1. Binary valued matrix has only two values in each cell : 0 and 1.
2. A submatrix is a matrix formed by selecting certain rows and columns from a larger matrix.
3. The area of a matrix with 'h' rows and 'w' columns is equal to 'h' * 'w'.

Problem approach

If the height of bars of the histogram is given then the largest area of the histogram can be found. This way in each row, the largest area of bars of the histogram can be found. To get the largest rectangle full of 1’s, update the next row with the previous row and find the largest area under the histogram, i.e. consider each 1’s as filled squares and 0’s with an empty square and consider each row as the base.
Run a loop to traverse through the rows.
Now If the current row is not the first row then update the row as follows, if matrix[i][j] is not zero then matrix[i][j] = matrix[i-1][j] + matrix[i][j].
Find the maximum rectangular area under the histogram, consider the ith row as heights of bars of a histogram. This can be calculated as given in this article Largest Rectangular Area in a Histogram
Do the previous two steps for all rows and print the maximum area of all the rows.

Try solving now

2. Convert a given Binary Tree to Doubly Linked List

Moderate

15m average time

80% success

0/80

Asked in companies

Given a Binary Tree, convert this binary tree to a Doubly Linked List.

A Binary Tree (BT) is a data structure in which each node has at most two children.

A Doubly Linked List contains a previous pointer, along with the next pointer and data.

The order of nodes in Doubly Linked List must be the same as Inorder of the given Binary Tree.

The doubly linked list should be returned by taking the next pointer as right and the previous pointer as left.

You need to return the head of the Doubly Linked List.

For the given binary tree :

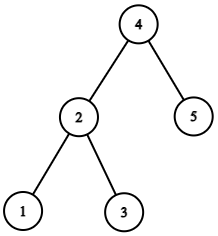
You need to return the head to the doubly linked list.
The doubly linked list would be: 1 2 3 4 5 and can be represented as:

Problem approach

The problem here is simpler as we don’t need to create a circular DLL, but a simple DLL. The idea behind its solution is quite simple and straight.

If the left subtree exists, process the left subtree
Recursively convert the left subtree to DLL.
Then find the inorder predecessor of the root in the left subtree (the inorder predecessor is the rightmost node in the left subtree).
Make the inorder predecessor as the previous root and the root as the next in order predecessor.
If the right subtree exists, process the right subtree (Below 3 steps are similar to the left subtree).
Recursively convert the right subtree to DLL.
Then find the inorder successor of the root in the right subtree (in order the successor is the leftmost node in the right subtree).
Make the inorder successor as the next root and the root as the previous inorder successor.
Find the leftmost node and return it (the leftmost node is always the head of a converted DLL).

Try solving now

Round

Easy

Video Call

Duration75 minutes

Interview date28 May 2022

Coding problem2

Basic introduction
Java related question(diff. b/w Hashmap and hashtable, multithreading, oops question

1. Design a stack that supports getMin() in O(1) time and O(1) extra space

Moderate

15m average time

85% success

0/80

Asked in companies

Create a stack data structure that allows operations such as push (adding an element), pop (removing the top element), top (retrieving the top element), and also provides a way to retrieve the minimum element in constant time.

Implement the following public functions :

1. push(data) :
This function should take one argument of type integer. It pushes the element into the stack and returns nothing.

2. pop() :
It pops the element from the top of the stack and returns nothing.

3. top() :
It returns the element being kept at the top of the stack.

4.  getMin() :
It returns the smallest element present in the stack.

Operations Performed on the Stack:

Query-1(Denoted by an integer 1): Pushes integer data to the stack. (push function)

Query-2(Denoted by an integer 2): Pops the data kept at the top of the stack. (pop function)

Query-3(Denoted by an integer 3): Fetches and returns the data being kept at the top of the stack. (top function)

Query-4(Denoted by an integer 4): Returns the smallest element present in the stack. (getMin() function)

Problem approach

We define a variable minEle that stores the current minimum element in the stack. Now the interesting part is, how to handle the case when minimum element is removed. To handle this, we push “2x – minEle” into the stack instead of x so that previous minimum element can be retrieved using current minEle and its value stored in stack. Below are detailed steps and explanation of working.
Push(x) : Inserts x at the top of stack.

If stack is empty, insert x into the stack and make minEle equal to x.
If stack is not empty, compare x with minEle. Two cases arise:
If x is greater than or equal to minEle, simply insert x.
If x is less than minEle, insert (2*x – minEle) into the stack and make minEle equal to x. For example, let previous minEle was 3. Now we want to insert 2. We update minEle as 2 and insert 2*2 – 3 = 1 into the stack.
Pop() : Removes an element from top of stack.

Remove element from top. Let the removed element be y. Two cases arise:
If y is greater than or equal to minEle, the minimum element in the stack is still minEle.
If y is less than minEle, the minimum element now becomes (2*minEle – y), so update (minEle = 2*minEle – y). This is where we retrieve previous minimum from current minimum and its value in stack. For example, let the element to be removed be 1 and minEle be 2. We remove 1 and update minEle as 2*2 – 1 = 3.

Try solving now

2. Maximum In Sliding Windows Of Size K

Moderate

20m average time

80% success

0/80

Asked in companies

Given an array/list of integers of length ‘N’, there is a sliding window of size ‘K’ which moves from the beginning of the array, to the very end. You can only see the ‘K’ numbers in a particular window at a time. For each of the 'N'-'K'+1 different windows thus formed, you are supposed to return the maximum element in each of them, from the given array/list.

Problem approach

Create a deque to store k elements.
Run a loop and insert first k elements in the deque. Before inserting the element, check if the element at the back of the queue is smaller than the current element, if it is so remove the element from the back of the deque, until all elements left in the deque are greater than the current element. Then insert the current element, at the back of the deque.
Now, run a loop from k to end of the array.
Print the front element of the deque.
Remove the element from the front of the queue if they are out of the current window.
Insert the next element in the deque. Before inserting the element, check if the element at the back of the queue is smaller than the current element, if it is so remove the element from the back of the deque, until all elements left in the deque are greater than the current element. Then insert the current element, at the back of the deque.
Print the maximum element of the last window.

Try solving now

Round

Easy

HR Round

Duration45 minutes

Interview date8 Jun 2022

Coding problem1

It was Hr round, around 3pm