Trainee Technology

You have been given an N*M matrix where there are 'N' rows and 'M' columns filled with '0s' and '1s'.

'1' means you can use the cell, and '0' means the cell is blocked. You can move in the 4 following directions from a particular position (i, j):

1. Left - (i, j-1)
2. Right - (i, j+1)
3. Up - (i-1, j)
4. Down - (i+1, j)

Now, for moving in the up and down directions, it costs you $1, and moving to the left and right directions are free of cost.

You have to calculate the minimum cost to reach (X, Y) from (0, 0) where 'X' is the row number and 'Y' is the column number of the destination cell. If it is impossible to reach the destination, print -1.

You are given an array consisting of N non-negative integers, and an integer K denoting the length of a subarray, your task is to determine the maximum elements for each subarray of size K.

Note:

A subarray is a contiguous subset of an array.

The array may contain duplicate elements.

The given array follows 0-based indexing.

It is guaranteed that there exists at least one subarray of size K.

You are given an array of size ‘N’ which is an array representation of min-heap.

You need to convert this min-heap array representation to a max-heap array representation. Return the max-heap array representation.

For Example

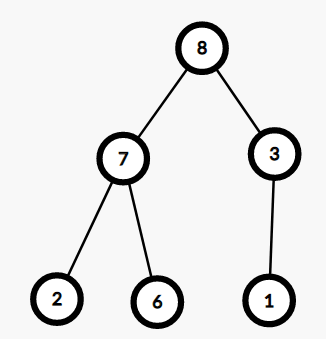
Corresponding to given min heap : [1,2,3,6,7,8]

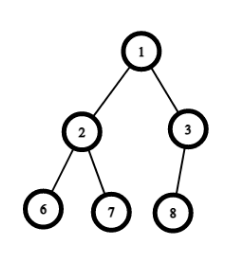
It can be converted to the following max heap: [8,7,3,6,2,1]

You are given a Singly Linked List which contains a series of integers separated by ‘0’.

Between two zeroes, you have to merge all the nodes lying between them into a single node which contains the sum of all the merged nodes. You have to perform this in place.

Note:

It is guaranteed that there will be no two consecutive zeroes, and there will always be a zero at the beginning and end of the linked list.

You have been given a Snake and Ladder Board with 'N' rows and 'N' columns with the numbers written from 1 to (N*N) starting from the bottom left of the board, and alternating direction each row.

For example

For a (6 x 6) board, the numbers are written as follows:

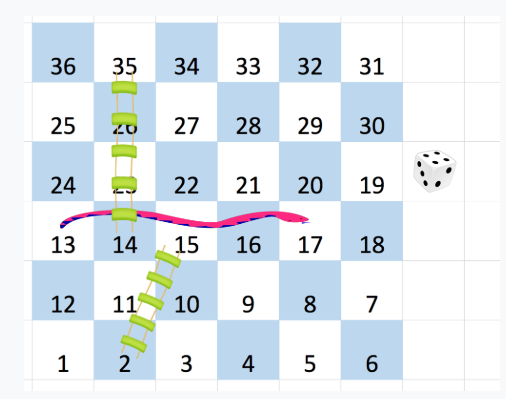
You start from square 1 of the board (which is always in the last row and first column). On each square say 'X', you can throw a dice which can have six outcomes and you have total control over the outcome of dice throw and you want to find out the minimum number of throws required to reach the last cell.
Some of the squares contain Snakes and Ladders, and these are possibilities of a throw at square 'X':
You choose a destination square 'S' with number 'X+1', 'X+2', 'X+3', 'X+4', 'X+5', or 'X+6', provided this number is <= N*N.
If 'S' has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.
A board square on row 'i' and column 'j' has a "Snake or Ladder" if board[i][j] != -1. The destination of that snake or ladder is board[i][j].

Note :

You can only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving - you have to ignore the snake or ladder present on that square.

For example, if the board is:
-1 1 -1
-1 -1 9
-1 4 -1
Let's say on the first move your destination square is 2  [at row 2, column 1], then you finish your first move at 4 [at row 1, column 2] because you do not continue moving to 9 [at row 0, column 0] by taking the ladder from 4.

A square can also have a Snake or Ladder which will end at the same cell.
For example, if the board is:
-1 3 -1
-1 5 -1
-1 -1 9
Here we can see Snake/Ladder on square 5 [at row 1, column 1] will end on the same square 5.