Introduction
Welcome to our blog on the topic 0-1 BFS (Breadth-First Search)! In this comprehensive blog, we delve into the intricacies and applications of this variant of the classic BFS algorithm. We will understand what it is and how it can be implemented.

For example:
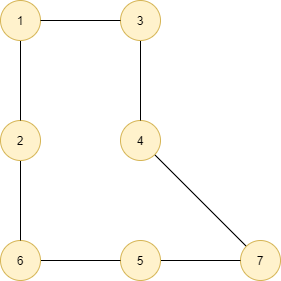
In the unweighted graph above, the shortest distance between the source node (1) and node (7) will be node1→ node3→ node4→node7 having 3 edges.
For the shortest path in a weighted graph, we consider the path having the minimum sum of their edge weights.
For example:
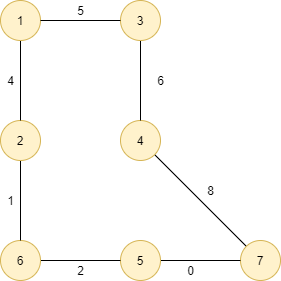
In the unweighted graph given above, there are two paths from the source node(1) to node(7):
- node1→ node3→ node4→node7 has a total edge weight of 19 units.
- node1→ node2→ node6→node5→node7 has a total edge weight of 7 units.
So, the shortest distance between the source node (1) and node (7) is node1→node2→ node6→node5→node7 having a total edge weight of 7 units.
We can use the Dijkstra algorithm for finding the shortest path in a weighted graph, which runs in O( E + VlogV ) time, but we can find a better solution if the weights are more constrained. This article will look at a better approach for solving the shortest path problem using a double-ended queue (Deque) called the 0-1 BFS algorithm, which works only when all edge weights are 0 or 1.
Also read, Euclid GCD Algorithm
0-1 BFS Algorithm
It is named 0-1 BFS because it only works for graphs with edge weights of 0 or 1. This type of BFS is used to calculate the shortest distance between the source node to all other vertices where the edges have weights of 0 or 1.
We will use deque (double-ended queue) in 0-1 BFS, which allows us to insert or delete elements from the front and back in O(1) time complexity.
- Traverse through all the nodes of the graph (source node will be pushed in the front of the deque, and then its neighbour nodes are pushed after popping the source node).
- Check the weight of all edges of the graph.
- Push the nodes into the deque, i.e. if the weight is 0, push it in the front of the deque else, push it to the back of the deque.
- Print the sum of the weight of edges, making the shortest path from the source node to other nodes.
Let’s understand this algorithm with an example:
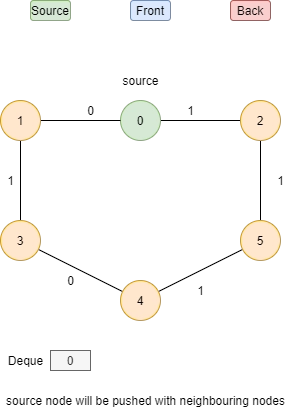
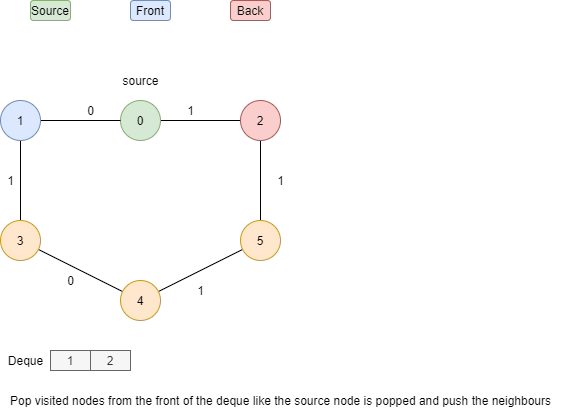
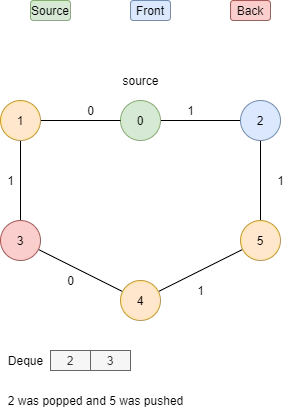
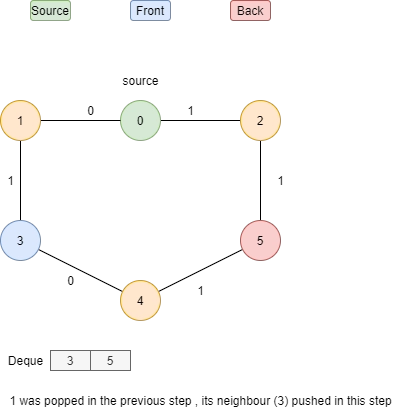
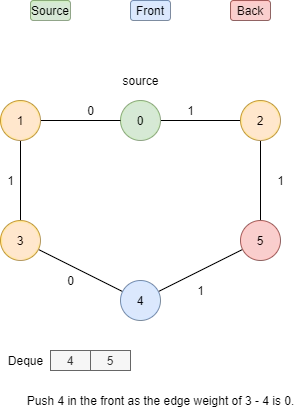
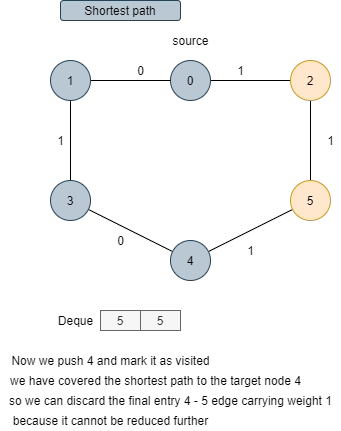
Basic code of 0-1 BFS(C++)
void ZeroOneBfs (int source)
{
deque <int> deq;
deq.push_back( source);
dist[ source ] = 0;
while ( !deq.empty ())
{
int v = deq.front( );
deq.pop_front();
for ( int i = 0 ; i < edges[v].size(); i++)
{
if (dist[ edges[ v ][ i ].first ] > dist[ v ] + edges[ v ][ i ].second )
{
dist[ edges[ v ][ i ].first ] = dist[ v ] + edges[ v ][ i ].second;
if (edges[ v ][ i ].second == 0)
{
deq.push_front( edges[ v ][ i ].first);
}
else
{
deq.push_back( edges[ v ][ i ].first);
}
}
}
}
}




