Table of contents

Introduction

Addition and Subtraction with Signed Magnitude Data

2.1.

Addition Algorithm

2.2.

Subtraction Algorithm

2.3.

Flowchart

2.4.

Hardware Implementation

2.5.

Example 1

2.5.1.

Solution

2.6.

Example 2

2.6.1.

Solution

Addition and Subtraction with Signed 2’s Complement Data

3.1.

Flowchart

3.2.

Hardware Implementation

3.3.

Example 1

3.3.1.

Solution

3.4.

Example 2

3.4.1.

Solution

Frequently Asked Questions

4.1.

What is the rule for addition and subtraction of signed numbers?

4.2.

How to add and subtract signed numbers?

4.3.

What is the law of signs in addition and subtraction?

Conclusion

Last Updated: Feb 14, 2025

Easy

Addition and Subtraction

Author Pranay Chauhan

Do you think IIT Guwahati certified course can help you in your career?

Yes

Introduction

We are taught how to conduct basic arithmetic operations in signed-magnitude representation from an early age. When the processes are carried out by hardware, this knowledge is extremely useful.

However, in order to carry out the operation and produce a correct result, the designer must be completely familiar with the sequence of actions that must be followed. An algorithm is a solution to a problem that is stated by a finite number of well-defined procedural steps.

When negative values are in signed-2's complement representation, an algorithm for adding two fixed-point binary numbers has been proposed. This is a simple algorithm to build because it only requires a parallel binary adder.

When negative numbers are represented in signed-magnitude form, the process becomes slightly more involved, requiring circuits to add and subtract as well as compare the signs and magnitudes of the numbers.

An algorithm usually consists of a series of procedural stages, each of which is dependent on the results of previous phases. A flowchart is a useful tool for presenting algorithms. Rectangular boxes represent the computational steps in the flowchart.

Inside diamond-shaped boxes, two or more alternate paths emerge, the decision stages are shown.

This article develops the various arithmetic algorithms and shows the procedure for implementing them with digital hardware. We consider addition and subtraction for the following types of data:

Fixed-point binary data in signed-magnitude representation
Fixed-point binary data in signed-2's complement representation

Computers employ a signed-magnitude approach to implement floating-point operations. Most computers utilise signed-2's complement approach for arithmetic operations on integers. The leftmost bit in the number is utilised to represent the sign in this technique; 0 denotes a positive integer, while 1 indicates a negative integer. The magnitude of the number was supported by the remaining bits in the number.

Also see, Difference Between Jfet and Mosfet

Addition and Subtraction with Signed Magnitude Data

Addition Algorithm

The addition algorithm specifies that:

If the signs of P and Q are the same, add both the magnitudes and put the sign of P to the result, as shown in the table below.
Compare both the magnitudes and subtract the small number from the greater number when the signs of P and Q disagree.
In cases where P > Q, the output signs must be equal to P, or the complement of P's sign in cases where P < Q.
Subtract Q from P and change the sign of the output to positive when the two magnitudes are equal.

Subtraction Algorithm

The subtraction algorithm states that:

When the signs of P and Q differ, the subtraction method says to add both the magnitudes and put the sign of P to the result.
Compare both the magnitudes and subtract the smaller number from the greater number when the signs of P and Q are the same.
In cases where P > Q, the output signs must be equal to P, or the complement of P's sign in cases where P < Q.
Subtract Q from P and change the sign of the output to positive when the two magnitudes are equal.

Operations	Addition of Magnitudes	Subtraction of Magnitudes
		P>Q	P<Q	P=Q
(+P) + (+Q)	+(P+Q)
(+P) + (-Q)		+(P-Q)	-(Q-P)	+(P-Q)
(-P) + (+Q)		-(P-Q)	+(Q-P)	+(P-Q)
(-P) + (-Q)	-(P+Q)
(+P) - (+Q)		+(P-Q)	-(Q-P)	+(P-Q)
(+P) - (-Q)	+(P+Q)
(-P) - (+Q)	-(P+Q)
(-P) - (-Q)		-(P-Q)	+(Q-P)	+(P-Q)

Flowchart

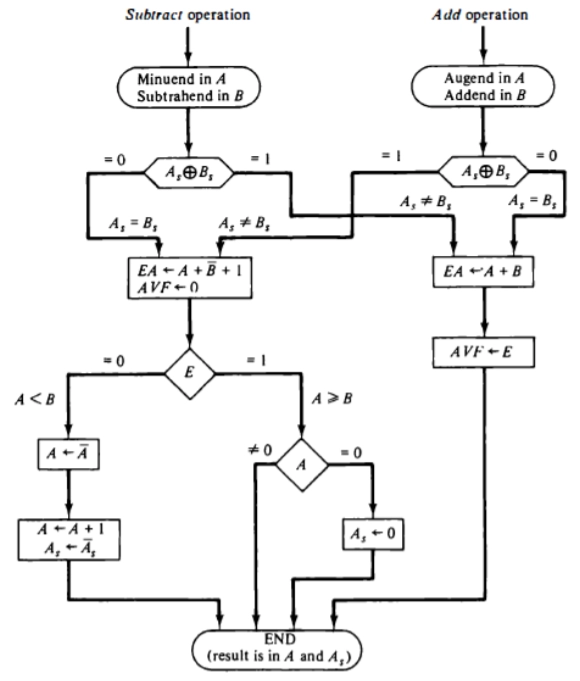
Flowchart for addition and subtraction

Hardware Implementation

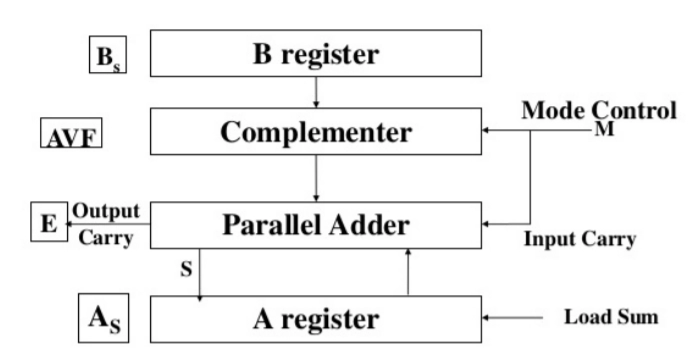
Hardware for signed-magnitude addition and subtraction

Example 1

Let's add two values, +3 and +2, using the signed magnitude representation.

Solution

We represent the given operands as shown below:

+3 = 0 0112

+2 = 0 0102

From the flowchart, we follow that A_s xor B_s = 0. This implies that A_s = B_s

Also, according to the table,

Operations	Addition of Magnitudes	Subtraction of Magnitudes
(+P) + (+Q)	+(P+Q)

So we do the addition of the magnitude of both operands.

Mag(+3) + Mag(+2) = 011₂ + 010₂ = 101₂ = Mag(5)

Now the sign of the result will be that of A_s

Therefore, +3 + (+2) = 0 101₂ = +5

Example 2

Let's subtract two values, +3 and +2, using the signed magnitude representation.

Solution

We represent the given operands as shown below:

+3 = 0 011₂

+2 = 0 010₂

From the flowchart, we follow that A_s xor B_s = 0. This implies that As = Bs

Also according to the table,

Operations	Addition of Magnitudes	Subtraction of Magnitudes
		P>Q	P<Q	P=Q
(+P) - (+Q)		+(P-Q)	-(Q-P)	+(P-Q)

Since the magnitude of P > Q,

We get results by +(P-Q).

Mag(Result) = 011 + (010)’ + 1 = 011 + 101 + 1 = (001)

SignBit(Result) = 0

Therefore, +3 - (+2) = +(+3-2) = +1

Also see, What Is a Motherboard and what is middleware

Addition and Subtraction with Signed 2’s Complement Data

Here, the signed-2's complement form of integers is examined, as well as arithmetic techniques for addition and subtraction. They've been summed up for your convenience. The sign bit is represented by the leftmost bit of a binary number: 0 for positive and 1 for negative. The full number is displayed in 2's complement form if the sign bit is 1. As a result, +33 is represented as 00100001, and -33 is represented as 11011111. The 2's complement of 00100001 is 11011111, and vice versa.

When two numbers are added in signed -2's complement form, the sign bits of the numbers are regarded the same as the other bits of the number. The sign-bit position's carry-out is disregarded.

The subtraction entails taking the subtrahend's 2's complement and then adding it to the minuend.

Flowchart

Algorithm for addition and subtraction in signed-2’s complement representation

Hardware Implementation

Hardware for signed-2’s complement addition and subtraction

Example 1

Let's use the 2's complement approach to add two decimal integers of +7 and +4.

Solution

The 2's complement representations of +4 and +7 with 5 bits each are shown below.

+7₁₀ = 00111₂

+4₁₀ = 00100₂

The addition of these two numbers is

(+7₁₀ ) + (+4₁₀ ) = 00111₂+ 00100₂

(+7₁₀ ) + (+4₁₀ ) = 01011₂

The resultant sum is 5 bits long. As a result, there is no carryover from the sign bit. The final total is positive, as shown by the sign bit '0'. In the decimal number system, the magnitude of the sum is 11. Therefore, the addition of two positive numbers will give another positive number.

Example 2

Let's use the 2's complement approach to subtract two decimal integers of +7 and +4.

Solution

The subtraction of these two numbers is

(+4₁₀ ) − (+7₁₀ ) = (+4₁₀ ) + (−7₁₀)

The 2’s complement representations of +4 and -7 with 5 bits each are shown below.

+4₁₀ = 00100₂

−7₁₀ = 11001₂

(+4₁₀ ) + (−7₁₀ ) = 00100₂ + 11001₂ = 11101₂

Here, carry is not obtained from the sign bit. The final total is negative, as shown by the sign bit '1'. As a result, we may determine the magnitude of the resultant sum as 3 in the decimal number system by taking 2's complement of it. Therefore, the subtraction of two decimal numbers, +4 and +7, is -3.

Must Read Shift Registers in Digital Electronics

Frequently Asked Questions

What is the rule for addition and subtraction of signed numbers?

Same signs: Add and keep the sign. Different signs: Subtract and take the sign of the larger absolute value.

How to add and subtract signed numbers?

For addition, add if signs match, subtract if different. For subtraction, change the sign of the second number and follow addition rules.

What is the law of signs in addition and subtraction?

Adding same signs keeps the sign. Adding opposite signs subtracts smaller from larger. Subtraction is converted into addition by changing the sign.

Conclusion

In this article, we learned about the addition and subtraction of signed numbers. We have discussed two ways of addition and subtraction of signed numbers. We also learned about the hardware implementation and the flowchart to carry out addition and subtraction. We also saw examples for the same.