Example of an Adjacency Matrix
Consider a graph with four vertices (A, B, C, D) and the following edges:
A → B
A → C
B → D
C → D
The adjacency matrix representation of this graph is:
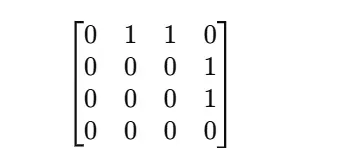
Graph Representation of the Adjacency Matrix
Here’s the graphical representation of the above matrix:
A → B
| |
↓ ↓
C → D
This matrix helps in efficient edge lookup, making it useful for dense graphs but less efficient in sparse graphs due to space complexity.
How to Build an Adjacency Matrix
Building an adjacency matrix is like filling out a chart where you mark who's friends with whom in a group. Let's say we have some points (we call them vertices), and some of them are connected by lines (we call these edges). We want to create a table that shows us all these connections at a glance.
Here's a step-by-step guide:
- List All Points: First, list down all the points (vertices) you have. If you have 5 points, label them something simple like A, B, C, D, & E.
- Create a Grid: Make a square grid where the number of rows & columns is the same as the number of points. Label the rows & columns with your points, so each cell in the grid has a pair of points.
- Fill in the Connections: Now, for each cell in your grid, think: "Is there a direct line between these two points?" If yes, put a 1 in that cell. If no, put a 0. Remember, if there's no line directly connecting two points, it's a 0.
Here's a simple example code to create an adjacency matrix for a graph with 4 vertices:
# Number of vertices
n = 4
# Create a matrix filled with 0's
adj_matrix = [[0 for _ in range(n)] for _ in range(n)]
# Add edges
# Let's say there's an edge between vertex 0 and 1
adj_matrix[0][1] = 1
# And an edge between vertex 1 and 2
adj_matrix[1][2] = 1
# Remember to add the reverse too if it's undirected
adj_matrix[1][0] = 1
adj_matrix[2][1] = 1
# Print the matrix
for row in adj_matrix:
print(row)
This code sets up a simple grid (matrix) & marks connections between points. It's like making a map of which cities are connected by roads directly.
Characteristics of the Adjacency Matrix
An adjacency matrix is like a big grid or table that shows us if there's a direct path between two points in a graph. Imagine you have a bunch of islands & some have bridges between them. The matrix helps you quickly check if you can go directly from one island to another without swimming!
Here's what makes the adjacency matrix special:
Simple to Understand
It's basically a table. If you've ever used a spreadsheet, you're halfway there. Each row & column represents a vertex (or point), and the cell where they meet tells you if there's a connection.
Zeroes & Ones
Mostly, we use 0s & 1s. A 0 means no bridge; a 1 means yes, there's a bridge. Easy, right?
Symmetry for Friends
In many cases, if you can go from A to B, you can also get back from B to A. This makes the matrix symmetrical, meaning it looks the same if you flip it around its diagonal.
Weighted Graphs
Sometimes, bridges have a weight limit or toll. We can put those numbers in the matrix instead of just 1s to show the cost or limit of each connection.
It's like having a map & a guidebook all in one, showing you all the direct routes & their conditions between the places you're interested in.
Applications of Adjacency Matrices
Adjacency matrices are like tools that help us understand connections. They are very useful in different areas. Let's look at some uses:
Maps and Routes
Imagine you have a map with cities and roads. Adjacency matrices can show which cities are directly connected by roads. This helps in planning trips or finding the shortest path from one city to another.
Social Networks
In social media, people are like points, and their friendships are like lines. An adjacency matrix can show who is friends with whom. This helps in seeing how people are connected.
Games
In some games, you move from one spot to another. An adjacency matrix can show where you can go from each spot. This helps in making game rules or finding ways to win.
Internet
Websites can be points, and links between them are lines. An adjacency matrix shows which websites link to each other. This helps in understanding how information spreads on the internet.
Biology
In studying genes or proteins, points can be different genes or proteins, and lines show how they interact. An adjacency matrix helps in seeing these connections, which is important for understanding how living things work.
Advantages of Using an Adjacency Matrix
An adjacency matrix, offers several advantages in representing relationships within a graph:
Efficient for Dense Graphs
In dense graphs where most vertices are connected, adjacency matrices excel. They provide a clear, concise representation of relationships between vertices without excessive space or computation.
Quick Edge Queries
Determining whether an edge exists between two vertices is a constant-time operation O(1)) with an adjacency matrix. This efficiency is valuable for algorithms that frequently check for edge presence.
Space Efficiency for Small Graphs
While adjacency matrices may consume more memory for large, sparse graphs, they are space-efficient for smaller graphs. Storing connections in a simple matrix structure minimizes overhead.
Straightforward Implementation
The concept of an adjacency matrix is intuitive and easy to implement. It mirrors the natural understanding of relationships between vertices, making it accessible for developers and students alike.
Efficient for Static Graphs
In scenarios where the graph structure remains static (i.e., no additions or deletions of vertices/edges), adjacency matrices offer optimal performance for tasks like pathfinding algorithms.
Disadvantages of Using an Adjacency Matrix
While an adjacency matrix is a handy tool for showing connections in a network, it's not perfect. Here are a few drawbacks:
Takes Up Space
Imagine you have a big room but only a few things to keep in it. That's what happens with an adjacency matrix when your graph doesn't have many connections. You end up with a big table full of 0s, wasting space.
Slow for Sparse Graphs
If your network is more like a long road with few crossroads, checking connections in a big matrix takes time. It's like flipping through a thick book just to find a few lines.
Adding or Removing Points is Tough
If you decide to add a new point or remove one, you have to redraw the whole table. It's like having to rewrite a whole page just to change one word.
Not Great for Complex Data
Sometimes, you need to know more than just if two points are connected. If your connections have different strengths or types, a simple 1 or 0 might not be enough.
Frequently Asked Questions
What are the applications of adjacency matrix?
Adjacency matrices are used in graph traversal, shortest path algorithms, network analysis, social network connections, circuit design, and biological network modeling.
What is the Rank of the Adjacency Matrix?
The rank of an adjacency matrix depends on the graph's structure and is at most equal to the number of vertices in the graph.
Where to Make an Adjacency Matrix?
Adjacency matrices are created in programming languages like C++, Python, and Java, and tools such as MATLAB, Excel, and network analysis software.
Is an adjacency matrix always square?
Yes, an adjacency matrix is always square because the number of rows & columns equals the number of vertices in the graph. Each row & column corresponds to a vertex, so the matrix must be square to account for all possible connections.
How do you identify isolated vertices in an adjacency matrix?
An isolated vertex, or a point with no connections, appears as a row & column of all 0s in the adjacency matrix. This means it has no edges connecting it to other vertices.
Conclusion
An adjacency matrix is a simple yet powerful tool to map out connections in a network, like friendships in a social network or routes in a transportation system. It has its perks, like being straightforward & great for dense networks. But it also has downsides, such as taking up unnecessary space in sparse networks & being a bit clunky when adding or removing vertices.






