Advanced Operators

Introduction

Let's ensure we understand the foundational concepts before delving further into the subjects. Here is a brief introduction if you are unfamiliar with Swift.

The multi-paradigm programming language Swift is compiled and can be used to create programs for iOS, OS X, tvOS, and watchOS. Apple Inc created it. It is an easy-to-learn language that is both strong and intuitive. Swift code is quick, accurate, and secure.

C, Objective-C, C++, and Swift code may all run in the same application thanks to Swift's foundation in the Objective-C runtime library. Since version 6, Swift, an open-source programming language, has been a part of Xcode.

This article explains the details of the Advanced operator in which we will talk about Bitwise NOT, AND, OR, XOR, and Left and Right Shift Operators.

Without further ado, let's get started.

Bitwise Operators

Bitwise operators let you work with the individual bits of unprocessed data within a data structure. They're frequently used in low-level programming, such as writing device drivers and graphics programs. Bitwise operators are especially helpful when working with unprocessed data from outside sources, for example, when encoding and decoding data for transmission via a unique protocol. The bitwise operators found in C are supported by Swift, as detailed below.

Bitwise NOT Operator

All of a number's bits are inverted by the bitwise NOT operator (~):

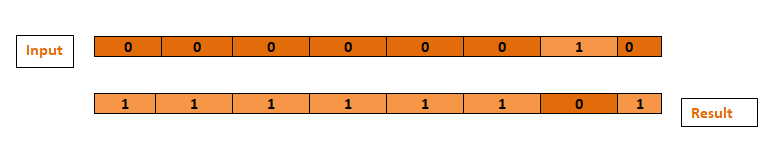
As a prefix operator, the bitwise NOT operator appears without a space right before the value it works on:

let x: UInt8 = 0b00000010
let y = ~x // equals 11111101

Eight-bit UInt8 integers may hold any value between 0 and 255. The binary number 00000010 is comparable to the number 2 in decimal form.

Then, a new constant called y that is identical to x but with all of the bits inverted is created using the bitwise NOT operator. Ones turn into zeros, and zeros turn into ones. The number 11111101, or 253 in unsigned decimal, is the value of y.

Bitwise AND Operator

Two numbers' bits are combined via the bitwise AND operator (&). Only when both of the input numbers' bits are equal to 1 does it return a new number with all of its bits set to 1:

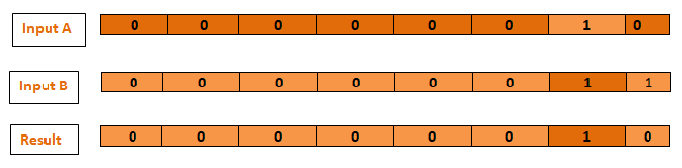
The x and y in the example below both have different bits. They are combined using the bitwise AND operator to form the integer 00000010, which is equivalent to the unsigned decimal value of 2:

let x: UInt8 = 0b00000010
let y: UInt8 = 0b00000011
let z = x & y // equals 00000010

Bitwise OR Operator

The bit comparison of two numbers is made using the bitwise OR operator (|). If either input number's bits are equal to 1, the operator produces a new number whose bits are 1:

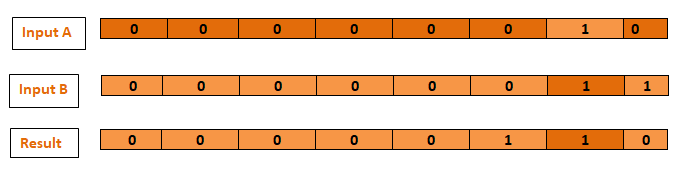
The values x and y in the example below have various bits set to 1. They are combined using the bitwise OR operation to form the integer 00000011, which has the unsigned decimal value of 3:

let x: UInt8 = 0b00000010
let y: UInt8 = 0b00000011
let z = x | y // equals 00000011

Bitwise XOR Operator

The "exclusive OR operator" (^), also known as the bitwise XOR operator, compares the bits of two numbers. When the input bits are distinct, the operator returns a new number whose bits are 1, and when they are identical, they are set to 0:

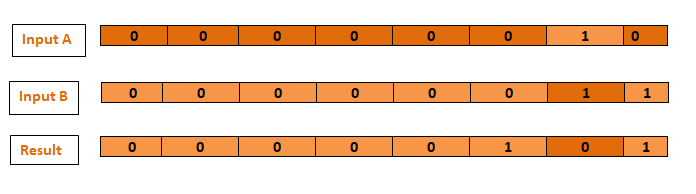
The x and y in the example below both have different bits. They are combined using the bitwise XOR operator to form the integer 00000001, which is equivalent to the unsigned decimal value of 1:

let x: UInt8 = 0b00000010
let y: UInt8 = 0b00000011
let z = x ^ y // equals 00000001

Bitwise Left and Right Shift Operators

According to the guidelines outlined below, the bitwise right shift operator (>>) and bitwise left shift operator (<<) shift all bits in a specific number of places to the left or right, respectively.

Shifting a bit in either the left or right direction has the same impact as multiplying or dividing an integer by two. An integer's value is doubled when its bits are shifted to the left by one, whereas its value is halved when they are shifted to the right by one position.

Shifting Behavior for Unsigned Integers

💁 For unsigned integers, the bit-shifting behaviour is as follows:

☑️ The required number of positions to the left or right shifts existing bits. 

☑️ Bits are discarded if they are moved outside the integer's storage range.

☑️ The spaces left behind after the initial bits are shifted to the left or right are filled with zeros.
 

This strategy is referred to as a logical shift.

The graph below displays the outcomes of operations 11111111 1 (which shifts 11111111 left by one spot) and 11111111 >> 1. Orange zeros are added, grey numbers are dropped, and blue numerals are moved:

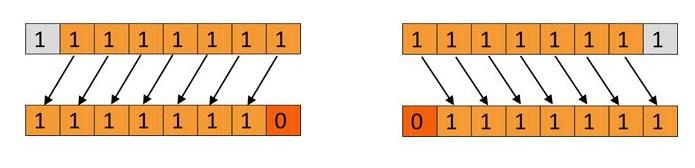
Bit shifting in Swift code looks like this:

let shift_Bits: UInt8 = 4 // 00000100 in binary
shift_Bits << 1 // 00001000
shift_Bits << 2 // 00010000
shift_Bits << 5 // 10000000
shift_Bits << 6 // 00000000
shift_Bits >> 2 // 00000001

Shifting Behavior for Signed Integers

Due to the binary representation of signed numbers, the shifting behavior is more complicated for signed than unsigned integers. (The examples following use 8-bit signed integers to keep things simple, but the concepts are the same for signed integers of any size.)

In signed integers, the first bit (sometimes referred to as the sign bit) indicates that the integer is either positive or negative. Positive and negative signs are represented by sign bits of 0 and 1, respectively.

The final bits, also called the value bits, hold the actual value. Similar to how unsigned integers are stored, positive numbers are stored by counting up from 0. The bits in an Int8 for the number 4 look like this:

The sign bit is 0, and the seven value bits represent the number 4 in binary (signifying "positive").

However, the way that negative numbers are stored varies. They are kept in memory by subtraction from 2 to the power of n, where n is the total amount of value bits. Seven value bits make up an eight-bit number; hence this equals 2 to the power of 7, or 128.

The bits in an Int8 look like this for the integer -4:

This time, the seven value bits have a binary value of 124 (128 - 4), and the sign bit is 1 (indicating "negative").

A two's complement representation is the name given to this method of encoding negative numbers. Although it may seem strange to express negative numbers, it provides many benefits.

First, you may add -1 to -4 by simply adding all eight bits (including the sign bit) in a regular binary operation, then deleting any data that doesn't fit in those eight bits once you're done:

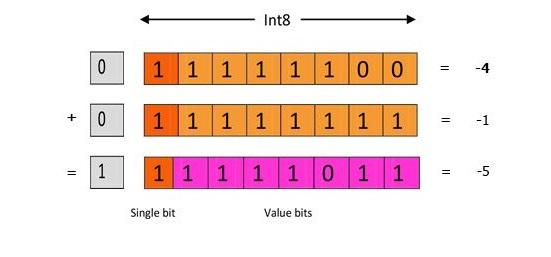
Second, by using the two's complement representation, you can shift the negative portions of numbers to the left and right just like positive portions, and you'll still end up doubling or halving them for each left or right shift. To do this, an additional rule must be followed when shifting signed integers to the right: When shifting signed integers to the right, follow the same rules as for unsigned integers, but fill any empty bits on the left with the sign bit rather than a zero.

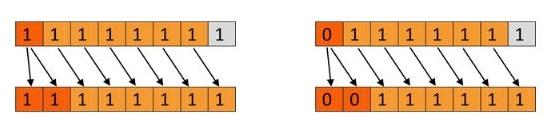
This operation, known as an arithmetic shift, ensures that signed integers have the same sign after being shifted to the right

Positive and negative integers are stored differently. Therefore moving either of them to the right brings them closer to zero. Negative numbers stay negative when their value approaches 0 by maintaining the sign bit during the shift.

Read about Bitwise Operators in C here.