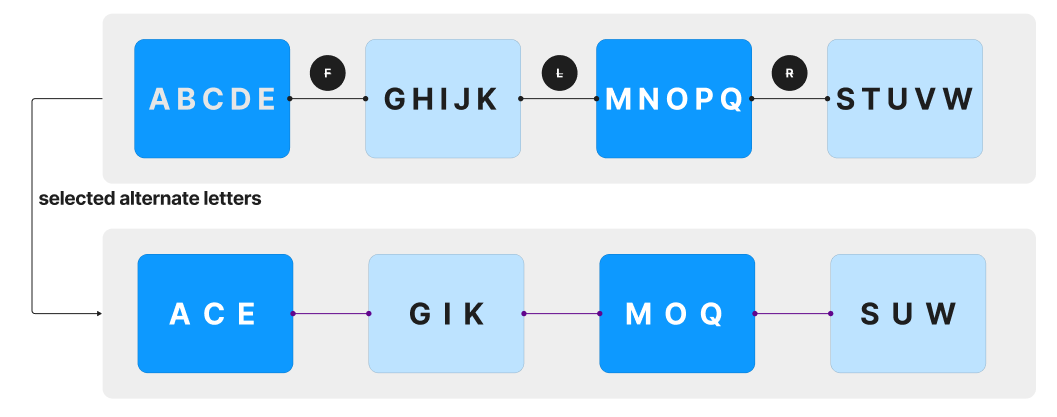
Introduction
Alphanumeric series is a sequence of characters containing either alphabets, numbers, or both. To solve the questions from the alphanumeric series, you need to be thorough with topics like Arithmetic Progression and Geometric progression. The questions asked from this topic are a mixed bag of coding-decoding, series-based reasoning, and position-based reasoning questions.

Alphanumeric series problems are asked in many competitive exams and the aptitude rounds of various companies. Hence, we will discuss it in detail in this blog.
Let us start by recalling the concepts of arithmetic progression and geometric progression. These concepts will help you in solving questions related to the alphanumeric series.
Arithmetic and Geometric Progression
A.P. and G.P. are fundamental concepts in the alphanumeric series. Some essential formulas of arithmetic and geometric progression are given below.
Arithmetic Progression
Arithmetic progression or A.P. is a series in which the difference between two consecutive terms remains constant.

Notations in Arithmetic Progression
In A.P., we will come across three main terms, denoted as:
-
Common difference (d)
-
nth Term (an)
-
Sum of the first n terms (Sn)
We talk about these properties in greater detail in the next section.
Common Difference in Arithmetic Progression
Suppose a1, a2, a3,…,an, is an Arithmetic Progression, then; the common difference "d" can be obtained as
d = a2 – a1
d = a3 – a2 and so on.
We can generalize the formula of common difference as:
| d = an – an-1 |
Here, "d" denotes the common difference. It can be negative, positive, or zero.
First Term of Arithmetic Progression
We can write the Arithmetic Progression in terms of common differences, as follows;
a, a + d, a + 2d, a + 3d, a + 4d, a+5d,…, a + (n – 1) d
Here, "a" is the first term of the progression.
General Form of an Arithmetic Progression
Consider an A.P.: a1, a2, a3,…, an.
| The general form of this A.P. will be: a + (n-1)d. |
The general form of this A.P. will be: a + (n-1)d.
Formula for the nth Term of an Arithmetic Progression
The formula for finding the nth term of an A.P. is:
| an = a + (n − 1) × d |
Sum of N Terms of Arithmetic Progression
We can compute the sum of the initial n terms of an Arithmetic Progression if the total number of terms and the first term are known. The formula for the sum of A.P. is given below:
Consider an A.P. consisting of “n” terms.
| Sn = n/2[2a + (n − 1) × d] |
Sum of Arithmetic Progression when the Last Term is Given
The formula to find the sum of A.P. when the first and last terms are given as follows:
| Sn = n/2 (first term + last term) |
Geometric Progression
A geometric progression (G.P.) is a sequence where every term contains a constant ratio to its preceding term.
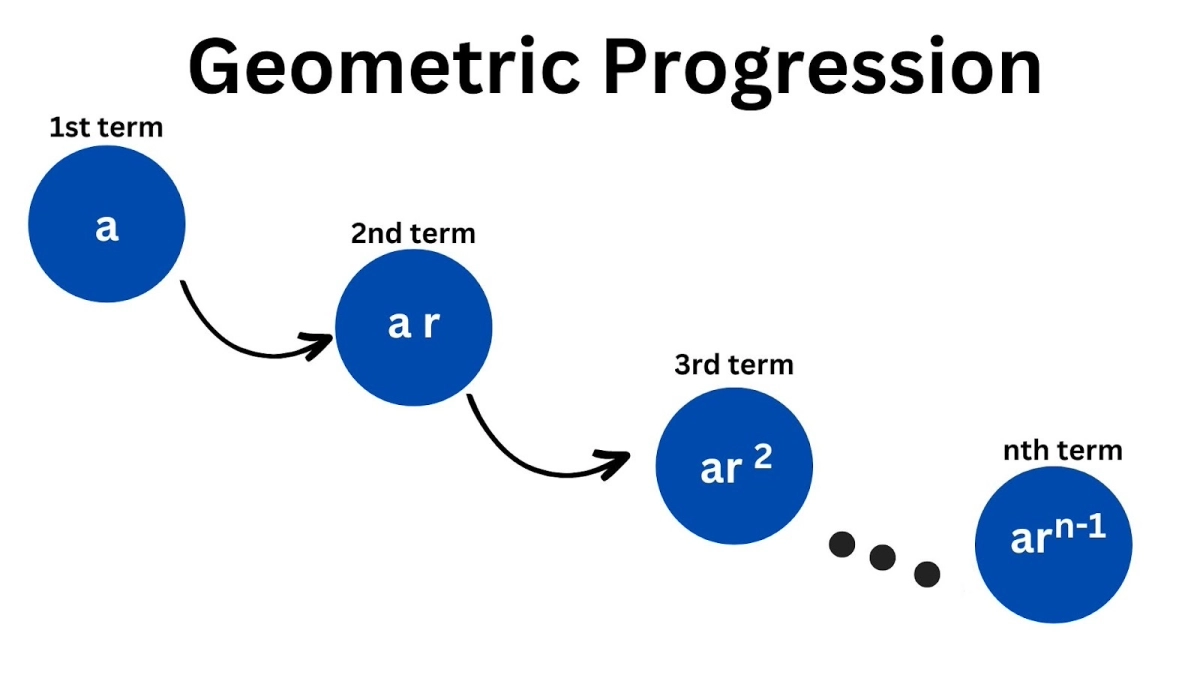
General Form
Geometric Progression is generally of the form: a, ar, ar2, ar3, ar4,…, arn-1
[Where a is the first term, r is the common ratio, n is the number of terms, and arn-1 is the nth term].
nth Term
Considering the general form of the geometric progression. Then,
First term; a1 = a
Second term; a2 = a × r
Third term; a3 = a2 × r = ar2
Similarly; an = arn-1
| nth term → an = arn-1 |
Note that the nth term is the last term of G.P.
Common Ratio
Considering the general form of the geometric progression.
Common ratio = (Any term) / (Preceding term)
= tn / tn-1
= (arn – 1 ) /(arn – 2)
| Common ratio = r |
Sum of n term
Considering the general form of the geometric progression.
Then the sum of n terms of G.P. is given by:
Sn = a + ar + ar2 + ar3 + ar4+…arn-1
The formula to find the sum of n terms of G.P. if the common ratio r ≠ 1 is:
| Sn = a[(rn-1)/(r-1)] |
Also, if the common ratio r = 1, then we can calculate the sum of the G.P. by:
| Sn = n*a |