Ambiguous Grammar

Introduction

Before heading towards ambiguous grammar, let's see about Context-Free Grammar. A context-free grammar is a formal grammar used to generate all the possible patterns of strings.

A context-free grammar is classified based on:

• Number of Derivation trees
• Number of Strings

The number of Derivation trees is further classified into

• Ambiguous grammar
• Unambiguous grammar

Let's have a detailed look at when grammar is ambiguous.

You can also read about - Moore Machine

Ambiguity in Grammar

A grammar or a Context-Free Grammar(CFG) is said to be ambiguous if there exists more than one leftmost derivation(LMDT) or more than one rightmost derivation(RMDT), or more than one parse tree for a given input string.

Technically, we can say that context-free grammar(CFG) represented by G = (N, T, P, S) is said to be ambiguous grammar if there exists more than one string in L(G). Otherwise, the grammar will be unambiguous.

One thing that should be transparent is that ambiguity is a property of grammar and not a language. 

Since Ambiguous Grammar can produce two Parse trees for the same expression, it's often confusing for a compiler to find out which one among all available Parse Trees is the correct one according to the context of the work. This is the reason ambiguity is not suitable for compiler construction.

Example 1

Let production rule is given as:

S -> AB|aaB 

A -> a|Aa 

B -> b 

Let us generate string aab from the given grammar. Parse trees for generating string aab are as follows : 

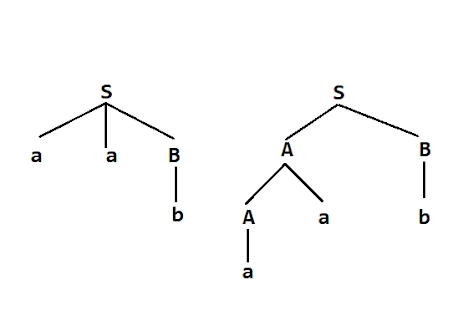
Here for the same string, we are getting more than one parse tree. Hence, grammar is ambiguous grammar. 

Example 2

Let production rule is given as: 

E -> EE+

E -> E(E)

E -> id 

Parse tree for id(id)id + is:

Only one parse tree is possible for id(id)id+, so the given grammar is unambiguous.

Also read - Arden's theorem

Example 3

Check the given production is ambiguous or not

S → aSb | SS  

S → ε  

For the string "aabb" the above grammar can generate two parse trees.

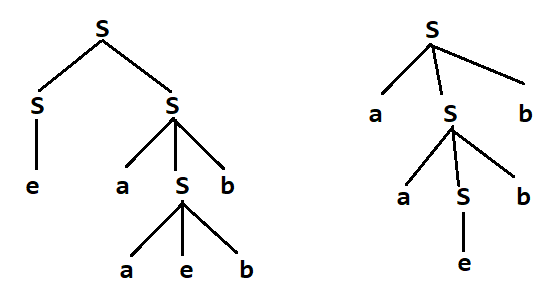
Since there are two parse trees for a single string, "aabb", the grammar G is ambiguous.

Note:

We can disambiguate a grammar such that only one derivation is possible for the string.

Inherently ambiguous for context-free grammar

If every grammar that generates L is ambiguous, then language is inherently ambiguous. eg for inherent grammar is L= {a^nb^nc^m}∪{a^nb^mc^m}.

Also see, Turing Machine in TOC.