Introduction
Amdahl's Law (or Amdahl's argument) is a formula in computer architecture that specifies the potential speedup in latency of task execution at a specific workload that may be expected of a system whose resources are increased. It is explicitly stated that "the total performance advantage realized by improving a particular portion of a system is restricted by the proportion of time that the enhanced part is used."

Digital computers were cutting-edge technology in the mid-1900s. Gene Amdahl graduated from the University of Wisconsin and joined IBM in 1952. Amdahl had already established a name for himself at UW by assisting in the design and construction of the WISC, or Wisconsin Integrally Synchronized Computer, the state's first digital computer.
Now let's see about Amdahl's Law in computer architecture in detail.
What is Amdahl's Law in Computer Architecture?
Amdahl's Law, formulated by computer architect Gene Amdahl, addresses the potential speedup of a program due to improvements in parallel processing. It states that the overall speedup from enhancing only a portion of a system is limited by the fraction of the program that remains sequential.
In other words, if a program has a segment that cannot be parallelized, no matter how much you speed up the parallelizable part, the overall improvement will be limited by the sequential part. Amdahl's Law serves as a critical guideline in optimizing parallel computing systems and underscores the importance of identifying and minimizing sequential bottlenecks in software and hardware design.
Also see, Difference Between Jfet and Mosfet and what is middleware
Amdahl's Law in Computer Architecture Formula
Amdahl's Law evaluates the predicted system speedup if one component is enhanced.
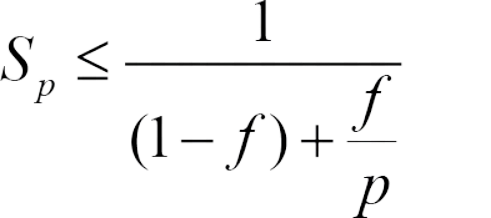
where,
- S is the expected speedup of the entire job execution;
- p denotes the speedup of the job that benefits from enhanced system resources;
-
f represents the fraction of execution time that the upgraded resource component initially occupied.
Also read, Microprogrammed control unit
Amdahl's Law in Computer Architecture Formula Derivation
A job performed by a system whose resources have been increased over a similar original system may be divided into two parts:
- a section that does not benefit from system resource improvement;
- a section that does benefit from system resource improvement
The computer software that handles files is one example. Some software may search the disk's directory and generate a list of files in memory. Following that, another section of the software sends each file to a different thread for processing. The scan of the directory and creation of the file list cannot be speed up on a parallel machine. However, the processing of the files may.
T denotes the execution time of the entire job before the enhancement of the system's resources. It comprises the execution time of the component that would not benefit from the resource optimization and the execution time of the part that would. The proportion of the task's execution time that would benefit from resource enhancement is represented by f. The one pertaining to the component that would not profit from it is, therefore, 1-f. Then:
T=(1-f )T+f T
It is the execution of the component that benefits from resource improvement that is expedited by the factor p following resource enhancement. As a result, the execution time of the portion that does not profit from it remains constant, while the execution time of the part that does benefit from it becomes:
(f/p)T
The theoretical execution time T(p) of the entire job after resource enhancement is then:
T(p)= (1-f)T + (f/p)T
Amdahl's Law offers the potential latency reduction of the entire job at a certain workload W, which produces
S(p)= TW/T(s)W= T/T(s)
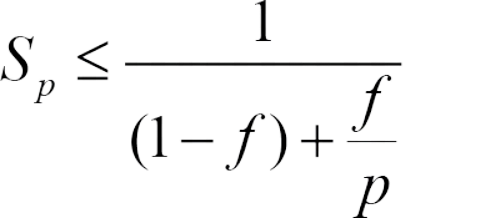
Relation of the Law of Diminishing Returns
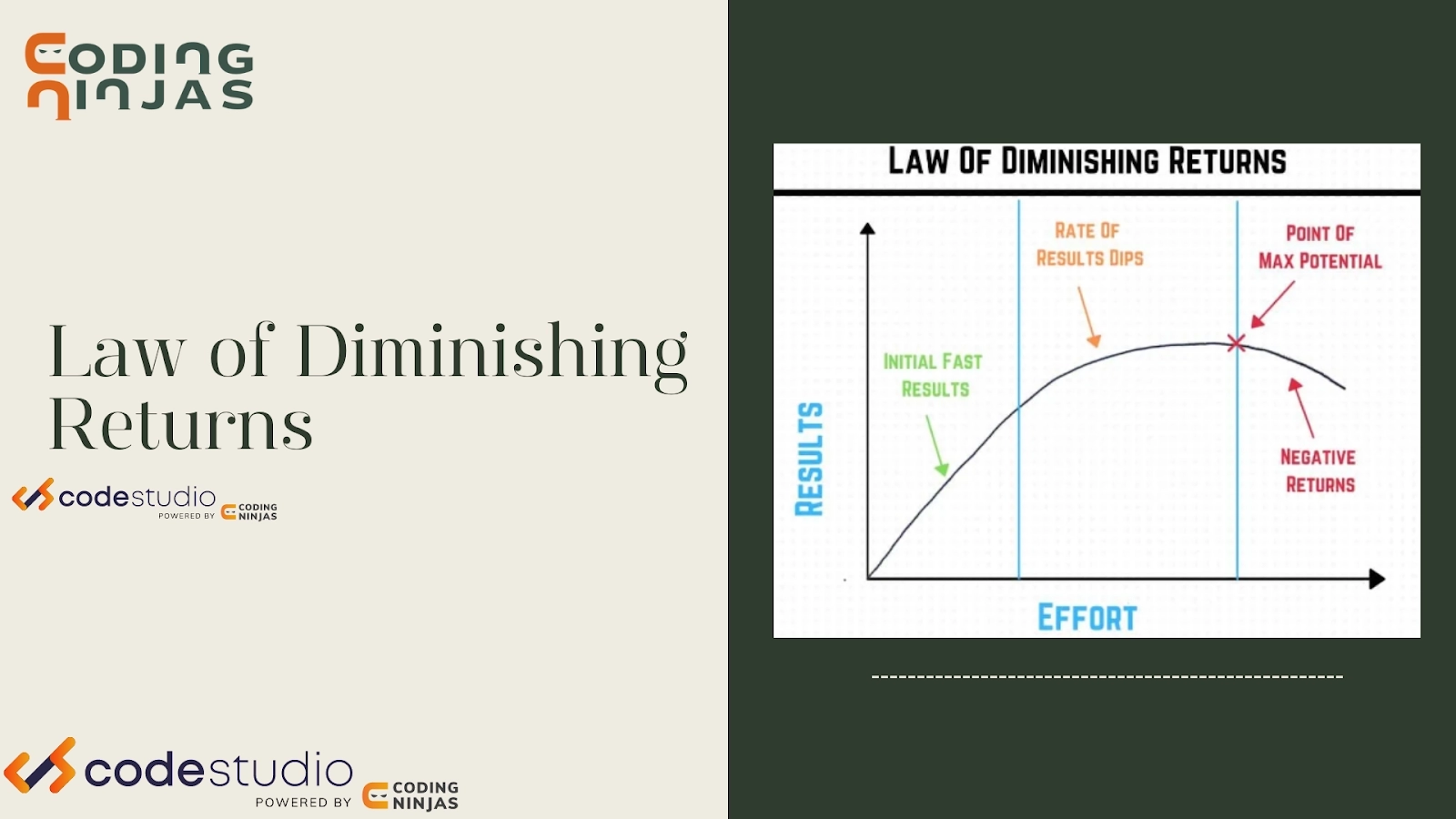
Amdahl's Law is sometimes confused with the Law of declining returns. However, only a specific application of Amdahl's Law exhibits the Law of diminishing returns. If one chooses what to enhance ideally (in terms of realized speedup), one will witness monotonically declining improvements as one improves. If, on the other hand, one chooses non-optimally, one can notice a rise in the return after improving a sub-optimal component and then going on to enhance a more optimal component. It is very important to note that it is frequently sensible to upgrade a system in a "non-optimal" order, given that certain changes are more difficult or need more development time than others.
If one considers what kind of return one receives by adding additional processors to a system and conducting a fixed-size computation that would employ all current processors to their capacity, Amdahl's rule does illustrate the Law of diminishing returns. Each subsequent CPU added to the system provides less useful power than the one before it. When the amount of processors is doubled, the speedup ratio decreases as the overall throughput approaches the limit of 1/(1- f).
Read About - Shift Registers in Digital Electronics and Cloud Computing.
Read Topic - Memory hierarchy in computer network, What are payloads





