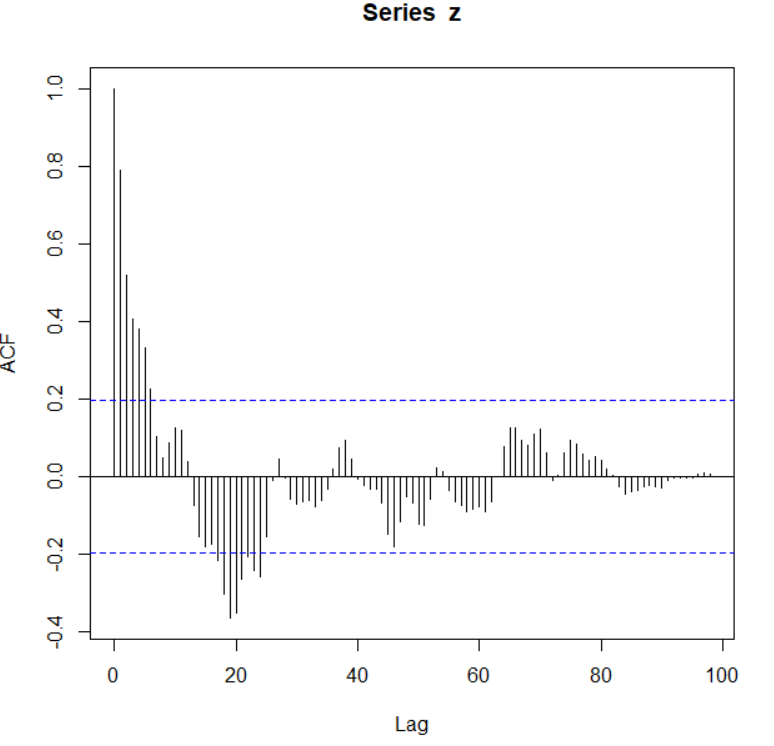
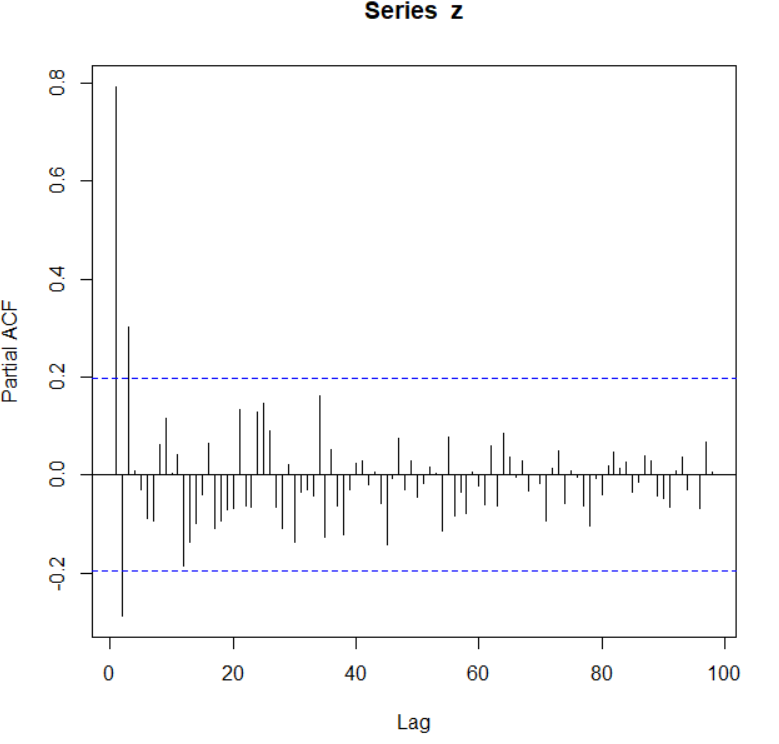
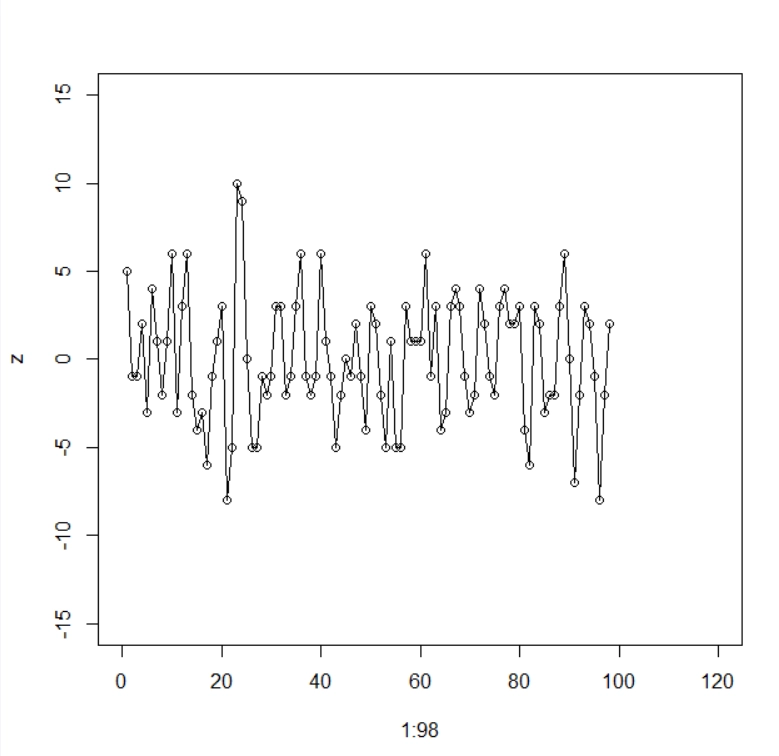
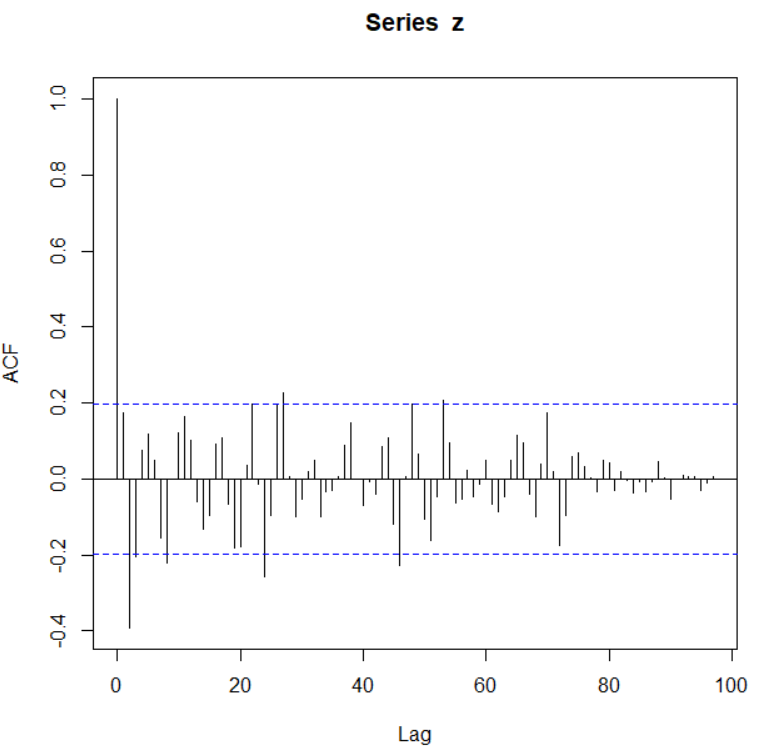
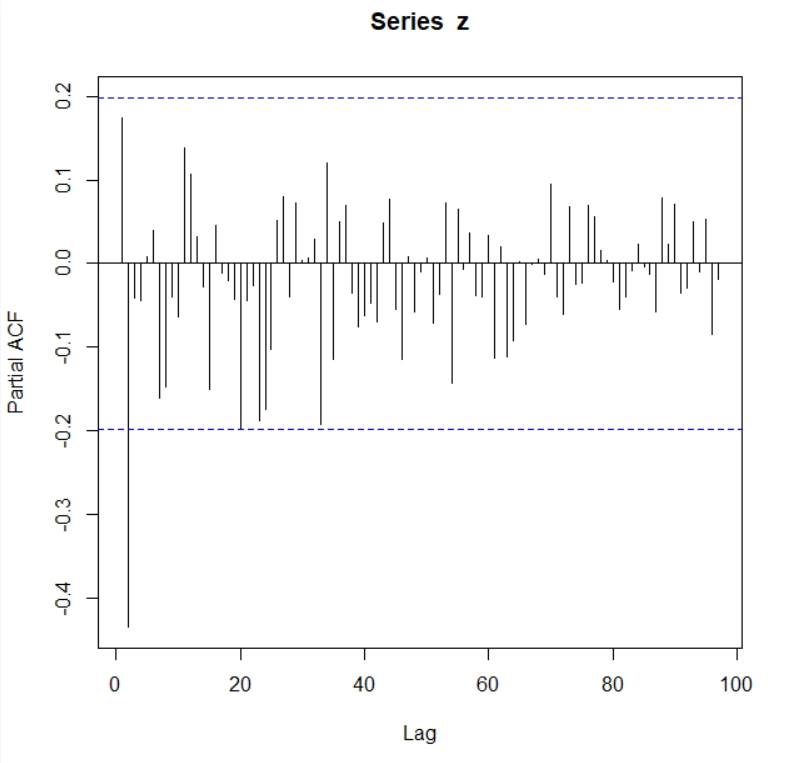
Introduction
Welcome Ninjas! Have there been times when you were watching a cricket match and guessed that this team might win based on its performance in previous matches? This is what Time Series Forecasting is all about, Predicting the future value based on the historical data we have.

In this blog, we will be learning about time series forecasting and a widely used approach, ARIMA, for the same. The blog will then follow the implementation and analysis of the ARIMA model.
Introduction to Time Series Forecasting
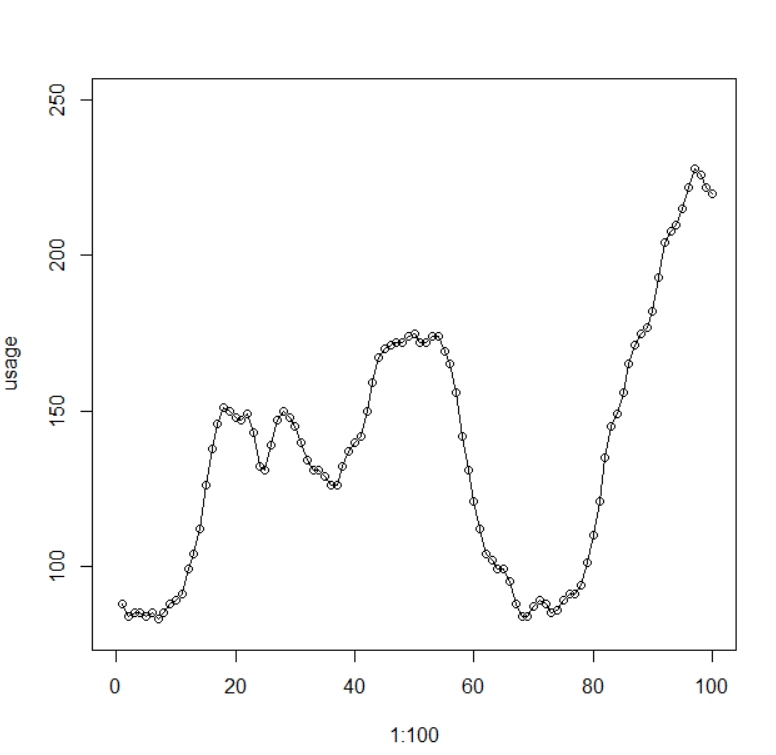
Time series forecasting refers to predicting future data based on historical data. Historical data is first analyzed. Then, the patterns(trends, cyclic patterns, etc.) are found and used in further prediction. In simpler words, we estimate the future value based on what has already happened.
Prediction problems involving a time component require time series forecasting. It provides a data-driven approach to effective and efficient planning.
Applications
Time Series is used in the study of various fields, some of them are mentioned below:
- Astronomy
- Business planning
- Control engineering
- Earthquake prediction
- Econometrics
- Mathematical finance
- Pattern recognition
- Resources allocation
- Signal processing
- Statistics
- Weather forecasting
Introduction to ARIMA
Now, What is the ARIMA model? ARIMA model is used as an approach for time series forecasting. The name ARIMA can be split into three parts:-
AutoRegression (AR)
AR tends to indicate the regression of a variable against itself, i.e., the output of a model is linearly dependent on its previous value. It also represents a type of random access.
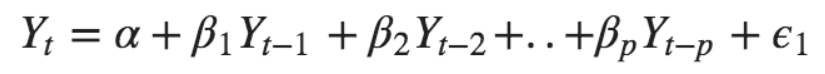
Moving Average (MA)
In a MA model, the output is linearly dependent on past forecast errors.
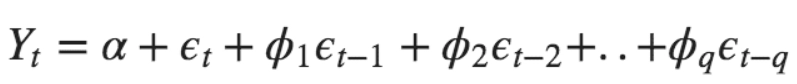
Where the error terms are based on errors from the equations given below:
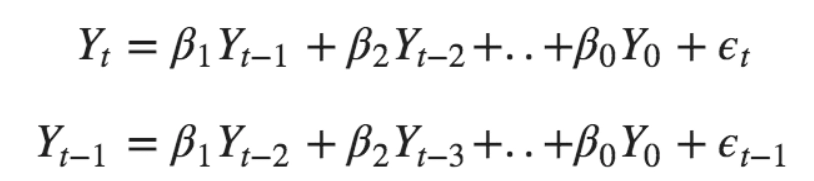
Moreover, when we combine the AR and MR terms, we get the equation:
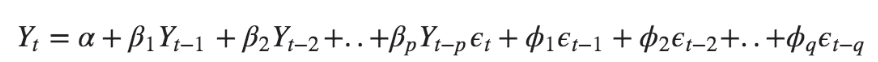
Integrated (I)
integrated refers to removing the trend and seasonal components. It is done to form stationary time series data.