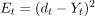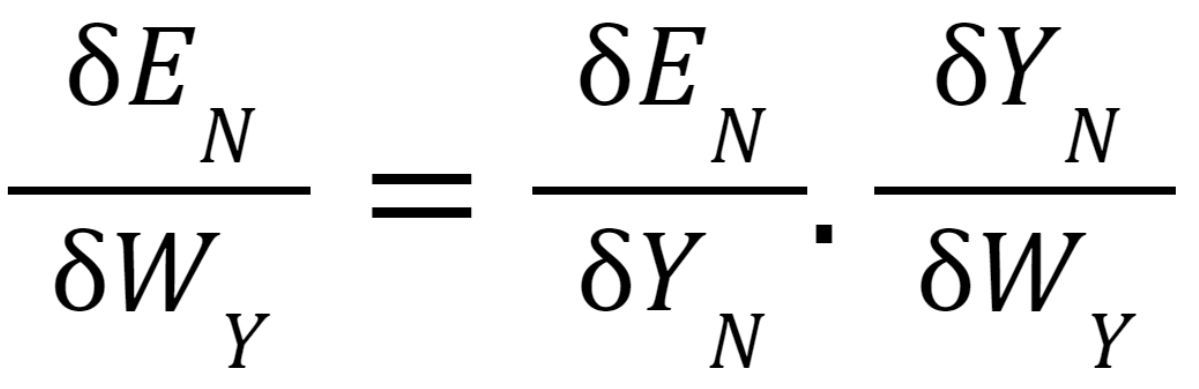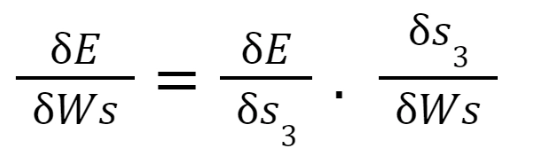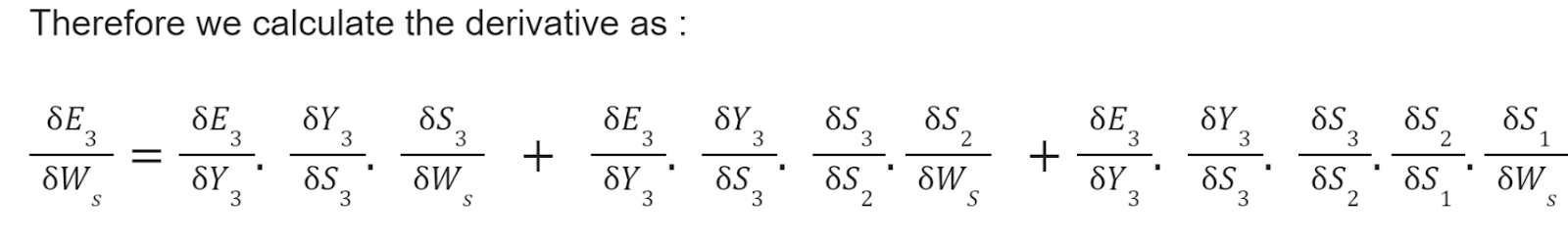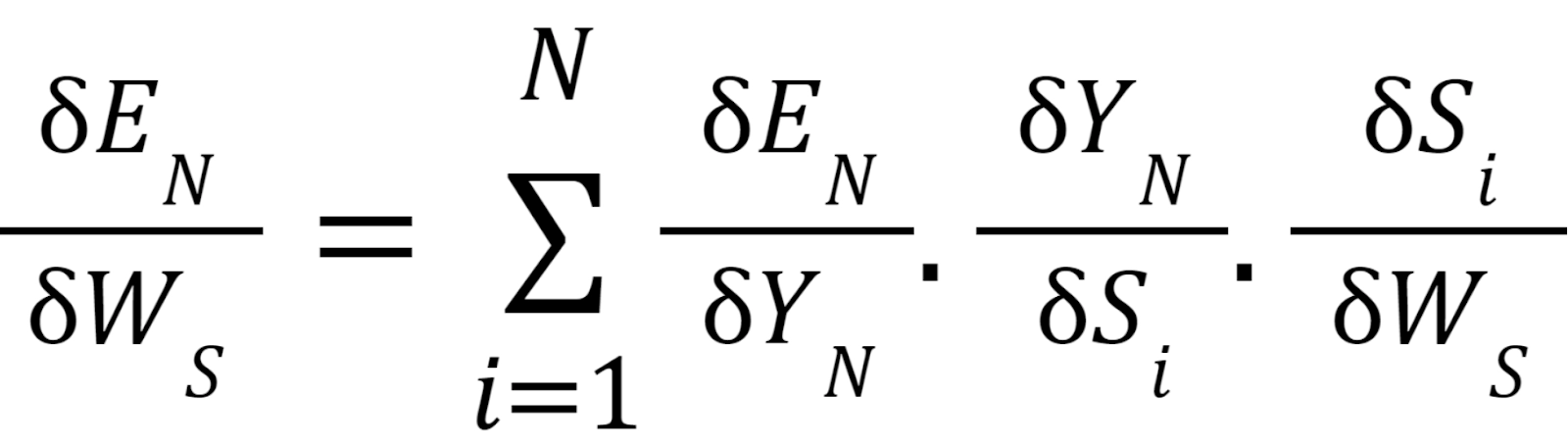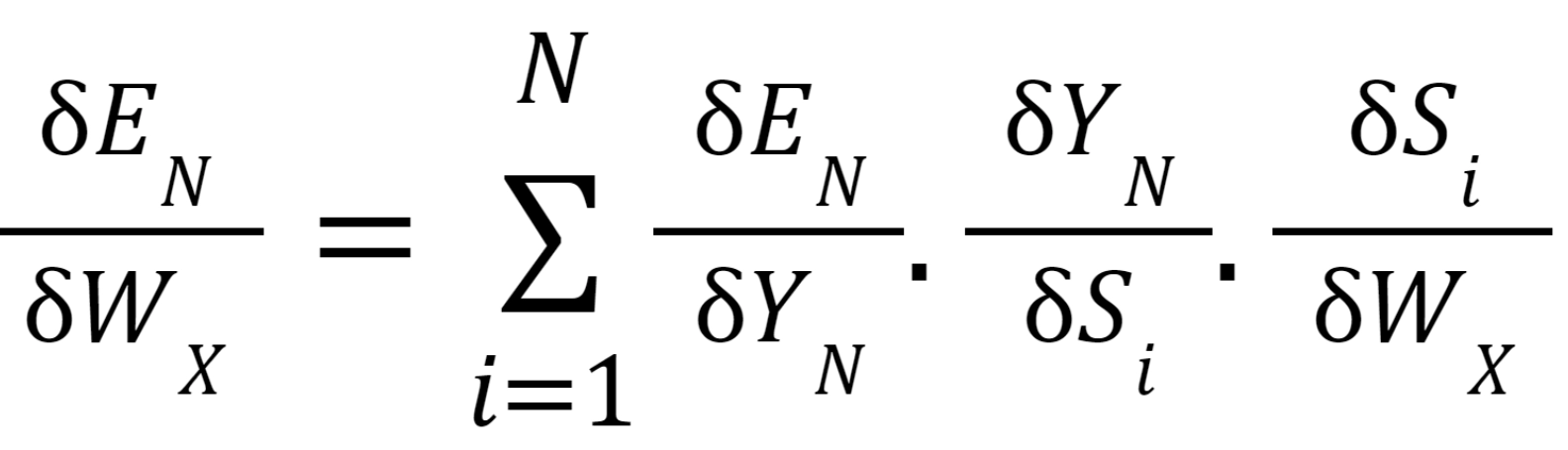Introduction
First, let us briefly go over Backpropagation. Backpropagation is a training algorithm that we use for training neural networks. When preparing a neural network, we are tuning the network's weights to minimize the error concerning the available actual values with the help of the Backpropagation algorithm. Backpropagation is a supervised learning algorithm as we find errors concerning already given values.
The backpropagation training algorithm aims to modify the weights of a neural network to minimize the error of the network results compared to some expected output in response to corresponding inputs.
The general algorithm of Backpropagation is as follows:
- We first train input data and propagate it through the network to get an output.
- Compare the predicted outcomes to the expected results and calculate the error.
- Then, we calculate the derivatives of the error concerning the network weights.
- We use these calculated derivatives to adjust the weights to minimize the error.
- Repeat the process until the error is minimized.
In simple words, Backpropagation is an algorithm where the information of cost function is passed on through the neural network in the backward direction. The Backpropagation training algorithm is ideal for training feed-forward neural networks on fixed-sized input-output pairs.
Unrolling The Recurrent Neural Network
We will briefly discuss RNN to understand how the backpropagation algorithm is applied to recurrent neural networks or RNN. Recurrent Neural Network deals with sequential data. RNN predicts outputs using not only the current inputs but also by considering those that occurred before it. In other words, the current outcome depends on the current production and a memory element (which evaluates the past inputs).
The below figure depicts the architecture of RNN :
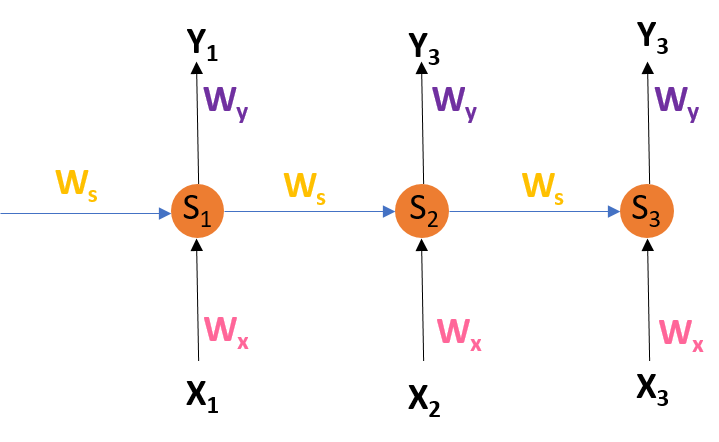
We use Backpropagation for training such networks with a slight change. We don't independently train the network at a specific time "t." We train it at a particular time "t" as well as all that has happened before time "t" like t-1, t-2, t-3.
S1, S2, S3 are the hidden states at time t1, t2, t3, respectively, and Ws is the associated weight matrix.
x1, x2, x3 are the inputs at time t1, t2, t3, respectively, and Wx is the associated weight matrix.
Y1, Y2, Y3 are the outcomes at time t1, t2, t3, respectively, and Wy is the associated weight matrix.
At time t0, we feed input x0 to the network and output y0. At time t1, we provide input x1 to the network and receive an output y1. From the figure, we can see that to calculate the outcome. The network uses input x and the cell state from the previous timestamp. To calculate specific Hidden state and output at each step, here is the formula:
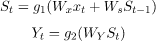
To calculate the error, we take the output and calculate its error concerning the actual result, but we have multiple outputs at each timestamp. Thus the regular Backpropagation won't work here. Therefore we modify this algorithm and call the new algorithm as Backpropagation through time.