Introduction
Hello ninjas. In this blog, we will discuss the concepts of backtracking and recursion and will also see the contrast between them. Recursion and backtracking are two of the most crucial algorithms and techniques for solving various problems.
Recursion can massively reduce the length and complexities of our code and is a more optimal approach against iteration. All sorts of tree and graph traversals and the famous Euclid's GCD(Greatest Common Divisor) can be efficiently done using recursion.
Backtracking is a technique which involves recursively finding solutions to a problem. It undoes the recursive changes if conditions are not met while discarding the less optimal ones to arrive at the best solution. It is a way more efficient technique than brute force. Though exponential in time complexity, backtracking is a fascinating approach that can easily solve the most complex problems of N-Queen and TSP(Travelling salesman problem).
Now, let's learn more about these techniques and conclude their differences.
What is Recursion?
Recursion is a phenomenon in computer science where a particular algorithm is repeated until it reaches its base case. In other words, when a function calls itself, it's called recursion.
It would be a lot simpler for the ones who have seen the movie Inception to understand the concept of recursion. As seen in the movie, Leonardo ambiguously has a dream. The character then has a dream inside the dream and has yet another dream, and this chain continues.
This can be theorised by taking a function dream() and repeatedly calling itself to eternity.
void dream()
{
cout << "Dream inside a dream" << endl;
dream();
}
Recursion follows a similar concept of a function repeatedly calling itself until it arrives at the base case.
When should we use Recursion?
Recursion is best used when a problem can be broken down into smaller, similar subproblems. It's particularly useful when the problem can be solved by solving smaller instances of the same problem. Use recursion when the problem naturally exhibits a recursive structure, such as tree traversal, divide and conquer algorithms, or problems that involve backtracking. However, it's important to consider the potential drawbacks of recursion, such as stack overflow for deeply recursive calls, and in some cases, recursion might not be the most efficient solution compared to iterative approaches.
Example
Recursion is used in solving problems that can break into smaller sub-problems of a similar kind. Let's take a simple example to understand how recursion functions. Let us find the factorial of a number.
Implementation in C++
- C++
C++
#include<bits/stdc++.h>
using namespace std;
int factorial(int x) {
// Base Case
if (x == 0)
{
return 1;
}
// Recursively calling the function
return x * factorial(x - 1);
}
// Driver Code
int main() {
int n;
cout<<"Enter the number: ";
cin>>n;
cout<<"Factorial of the number= "<<factorial(n);
return 0;
}
Output:
Flowchart
The flow chart shows how recursion works for factorial(4):
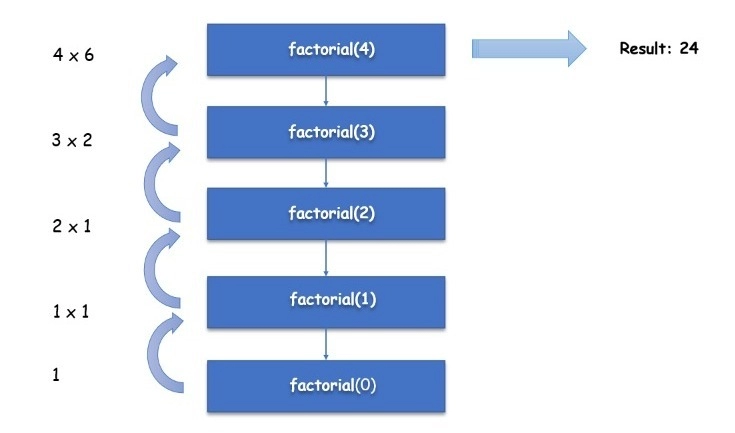
Base Case
Every recursive function has a terminating condition called the base case. The base case condition is the one for which the answer is already known, we know the answer for that condition, and we need to return it.
So here, in this problem, we know that factorial(0) = 1, so when x is equal to zero, we return one.
Else we break into smaller sub-problem, i.e., factorial(x-1).
If we don't include the base case, the function will keep calling itself and never end.
Time Complexity
For the base, the time complexity, i.e., the time complexity f(0), is 1, which can be computed in 1 unit of time because there is only one comparison.
Still, in the general case for factorial(n), there is only one comparison and, one multiplication, one subtraction. Therefore, the time complexity can be computed in 3 units of time.
So the recurrence relation can be written as:
T(n) = 1 {where, n=0}
and
T(n) = T(n-1) + 3
= T(n-2) + 6
= T(n-3) + 9
= …..
= T(n-k) + 3k
Substitution method:
If k=n, then,
T(n) = T(0) + 3n, (as, k=n)
= 1 + 3n
Therefore, the time complexity is O(n).
Space Complexity
For every call in the recursive function, the call is saved in the program stack till the value is computed and returned to the function.
f(5) → f(4) → f(3) → f(2) → f(1) → f(0)
f(5) → f(4) → f(3) → f(2) → f(1)
f(5) → f(4) → f(3) → f(2)
f(5) → f(4) → f(3)
f(5) → f(4)
f(5)
As you can see from the above picturisation, the f(5) will require a stack of size five to store all the calls from 5 to 1.
Since n calls will be stored at max in the stack, the space complexity would be O(n).
Advantages of Recursion
The advantages of Recursion are:
- Concise code: Recursion can lead to more elegant and concise solutions, especially for problems with recursive structures.
- Simplified logic: It often simplifies the logic of algorithms by allowing the problem to be broken down into smaller, more manageable parts.
- Handling nested structures: Recursion is well-suited for handling nested data structures like trees and graphs.\
- Facilitates divide and conquer: It's integral to the divide and conquer paradigm, making it useful for solving problems like sorting and searching.
Disadvantages of Recursion
The disadvantages of Recursion are:
- Stack overflow: Deeply recursive functions can lead to stack overflow errors due to the limited size of the call stack.
- Performance overhead: Recursion can introduce performance overhead compared to iterative solutions due to function calls and stack manipulation.
- Debugging complexity: Recursive functions can be harder to debug and understand, especially when dealing with multiple recursive calls and base cases.
- Memory consumption: Recursive function calls consume additional memory for maintaining the call stack, which might not be efficient for large problem instances.
Applications of Recursion
The applications of Recursion are:
- Tree and graph traversal: Recursion is commonly used for traversing tree and graph structures, such as in depth-first search and tree traversal algorithms.
- Dynamic programming: Many dynamic programming algorithms involve recursion to break down a problem into smaller subproblems and memoize the results.
- Backtracking: Recursive backtracking algorithms are used to exhaustively search for solutions to combinatorial problems like the N-queens problem or Sudoku.
- Divide and conquer: Recursion is fundamental to divide and conquer algorithms like merge sort, quicksort, and binary search, which exploit the recursive nature of the problem to efficiently solve it.
![second queen at {4, 2]](https://files.codingninjas.in/article_images/backtracking-and-recursion-8-1673349225.webp){kind=tracking}
46+ registered 