Introduction to Basic Logical Operations
A logical operation is a symbol or word that joins two or more information phrases. It's most commonly used to see if a connection between two sentences is true or untrue.
Logical operations are required in computing because they mimic the flow of information across electrical circuits, such as those found within a CPU. These operations are known as boolean operations.
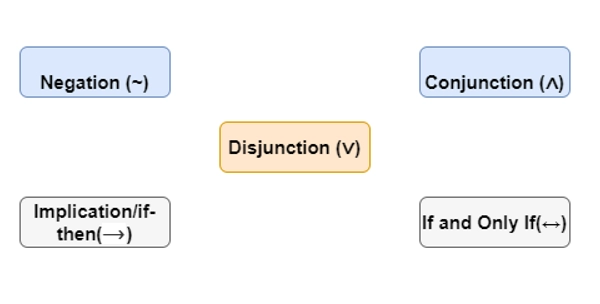
Basic logical operators
Negation
It has the exact opposite meaning as the original sentence. If R is a statement, then ~R denotes the negation of R, which is read as 'it is not the case that R.' As a result, if R is true, ~R is false, and vice versa.
For example, if there is statement R, pizza contains cheese, then ~R will denote pizza that does not contain cheese.
| R | ~R |
| T | F |
| F | T |
Conjunction
It refers to the combining of two assertions. If R and S are two statements, then "R and S" is a compound statement represented by R ∧ S and referred to as "R and S conjunction." Only when both R and S are true the combination of R and S is true. Otherwise, it's false.
| R | S | R ∧ S |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Disjunction
Or-ing two statements are what it means. If R and S are two assertions, then "R or S" is a compound statement indicated by R ∨ S and referred to as the R and S disjunction. When at least one of the two propositions is true, the disjunction of R and S is true, and when both R and S are false, it is false.
| R | S | R ∨ S |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Implication/if-then
The assertion "if R, then S" is an implication R⟶S. If R is true and S is false, it is false; otherwise, it is true.
| R | S | R⟶S |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | F |
If and Only If
R↔S is a bi-conditional logical connective that holds true when R and S are the same, i.e., when both are false or true.
| R | S | R ∨ S |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | F |
Derived Connectors
Some of the Derived Connectors are as follows.
NAND
It denotes negation after two assertions have been ANDed. Assume there are two propositions, R and S. The nanding of R and S is a statement that is false when both R and S are true, but true otherwise. R ↑ S is the symbol for it.
| R | S | R ↑ S |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
NAND Symbol
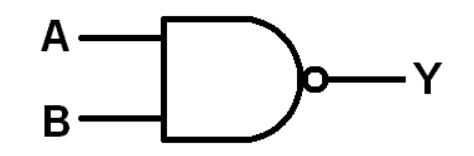
NOR or JOINT DENIAL
It refers to the negation of two assertions after they have been OR. Assume there are two propositions R and S. NORing R and S to get a claim that is true when both R and S are false, otherwise false. R ↓ S is the symbol for it.
| R | S | R ↓ S |
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
NOR Symbol
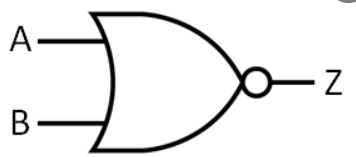
XOR
Assume there are two propositions, R and S. If R or S is true but not both, XORing them is true, and vice versa. R⨁S is the symbol for it.
| R | S | R ⨁ S |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
XOR Symbol
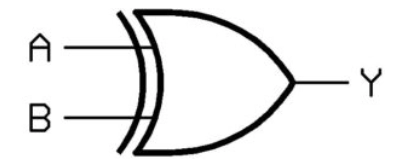
Examples
Example 1: Prove that ~(X ⨁ Y) ≅ (~X ∧∼Y)∨(X∧Y).
| X | Y | X⨁Y | ~(X⨁Y) | ~X | ~Y | ~X∧~Y | X∧Y | (~X ∧∼Y)∨(X∧Y) |
| T | T | F | T | F | F | F | T | T |
| T | F | T | F | F | T | F | F | F |
| F | T | T | F | T | F | F | F | F |
| F | F | F | T | T | T | T | F | T |
We can see that the truth table of ~(X ⨁ Y) is equal to (~X ∧∼Y)∨(X∧Y), hence both of them are equal. Hence proved.
Example 2: Prove that (X ⨁Y) ∨ (X ↓ Y) ≅ X↑ Y
| X | Y | X⨁Y | X ↓ Y | (X ⨁Y) ∨(X↓Y) | X↑ Y |
| T | T | F | F | F | F |
| T | F | T | F | T | T |
| F | T | T | F | T | T |
| F | F | F | T | T | T |
We can clearly see that both the tables (X ⨁Y) ∨ (X ↓ Y) and X↑ Y are equal, hence proved.
Frequently Asked Questions
The operator that reverses the truth table of the operation?
Not operator is used to reverse the truth table of the operation.
The operator that returns true if all sub-conditions are true?
And operator gives true if all sub condition is true, otherwise it gives false if any of the condition is false.
The operator that returns true if any sub-conditions are true?
Or operator gives true if any sub condition is true, otherwise, it gives false if all conditions are false.




