Introduction
Before proceeding with the Boyce-Codd Normal Form, review these topics to gain a better understanding of the database normalization concept:
Boyce-Codd normal form is an extension of the third normal form. It is stricter as an advanced version of 3NF, and most of the redundancy based on functional dependency is removed. The Boyce Codd Normal Form is also called the 3.5 Normal Form.
The third normal form is usually adequate for relations to reduce redundancy, but since it does not eliminate 100% of the redundancy, there is an ideal version we can work towards, i.e., the BCNF.
In this article, we’ll be looking at what exactly BCNF entails and how to convert a table into BCNF if not.
Key Terms Required to Understand BCNF
🌟 Prime-attributes: A column that is a part of some candidate key is called a prime attribute.
🌟 Superkey: A super key is an attribute or set that uniquely identifies data items in a table. Superkey attributes can contain null values too, which is not the case for a primary key.
🌟 Functional dependency: It is a constraint specifying the relationship between two attributes where one attribute helps determine the value of the other. Functional dependency is denoted as X → Y. Here, X(determinant) is a set of attribute(s) that can help determine the value of Y(dependent).
🌟 Determinant: The set of attributes to the left of the arrow that helps determine the value of the other attributes is called the determinant. In X→Y, X is the determinant.
🌟 Dependent: The attribute to the right of the arrow, whose value is determined by the determinant is called the dependent. In X→Y, Y is the dependent.
🌟 Trivial functional dependency: A dependent will always be a subset of the determinant in this type of functional dependency. This means that if X → Y is in trivial functional dependency, then Y will be the subset of X. For example, in a table with the attributes empID and empName, {empID, empName} → empName is a trivial functional dependency because the dependent is a subset of the determinant set {empID, empName}. Similarly, empID→ empID is also a trivial functional dependency.
🌟 Non-trivial functional dependency: The dependent, in this case, is strictly not a subset of the determinant. This means that if X → Y is in non-trivial functional dependency, Y will not be a subset of X.
Rules for BCNF
Before we move forward with the rules let us first discuss from where the BCNF originated. BCNF was created as an extension to the 3NF, in 1974 by Raymond Boyce and Edgar Codd. The men were working to create Database schemas that minimise redundancies with the goal of reducing computational time. The third normal form eliminates columns that are not dependent on the primary key in addition to meeting the guidelines in the 1NF and 2NF. BCNF, which is often referred to as 3.5NF, meets all the requirements of 3NF and requires that candidate keys not have any dependency on other attributes in a table.
Let us now discuss the rules for the same:
A table will be in Boyce Codd Normal Form if:
💥 First, it is in the third normal form(3NF).
👉 For a table to be in 3NF, there must be no transitive dependencies. When a dependent is indirectly dependent on the determinant, it is a transitive functional dependency. This means that if a → b and b → c, then a → c.
💥 Second, A must be a super key for a dependency A → B.
👉 This part may look tricky but isn’t. We’ve encountered the cases where Non-prime attributes are determining Non-prime attributes and Prime-attributes are determining the non-prime attributes. But what if a non-prime attribute determines the prime attribute. To conclude the point, for a dependency A -> B, A must not be a non-prime attribute if B is a prime attribute in order to be in BCNF.
Demo Table
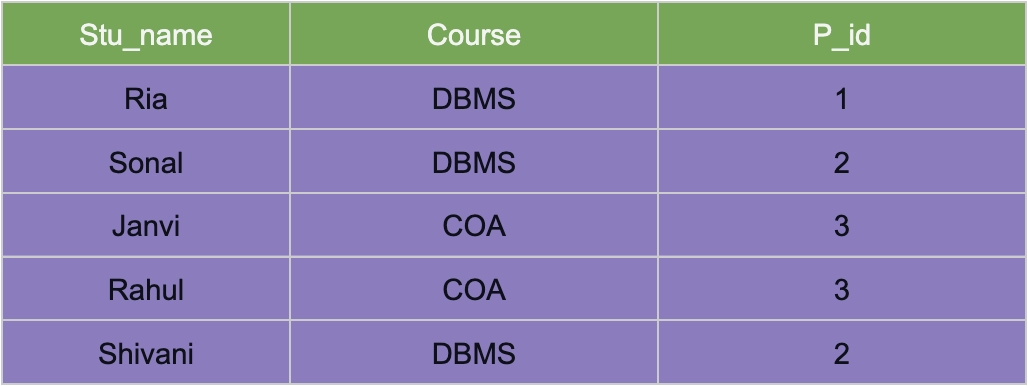
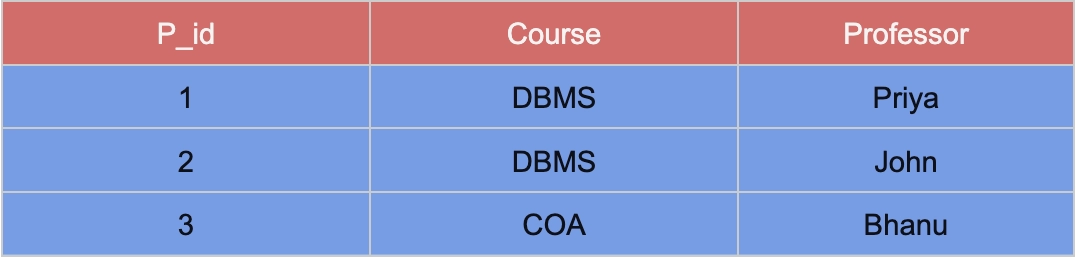
Below is an example of a course enrollment table wherein respected course and professor’s data is present:
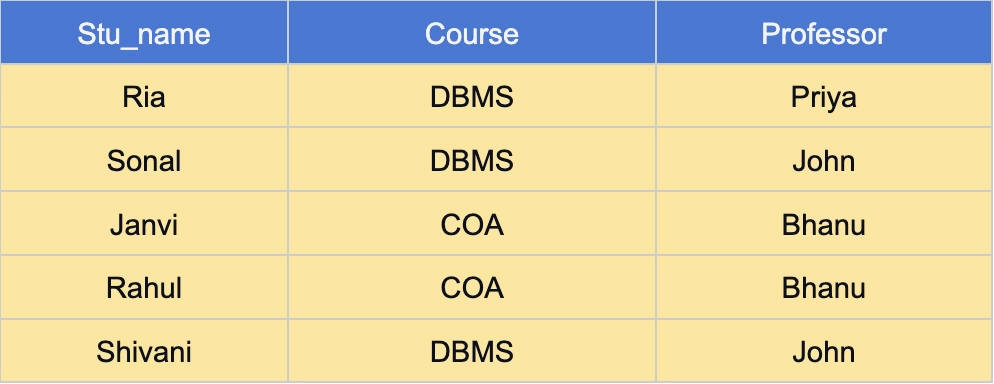
In the above table:
✍️ Each student can enrol in multiple courses. Although in the above representation there is no such case, it might be possible.
✍️ For each subject, there can be multiple professors. For example, DBMS is taught by two professors Priya and John.
What do you think should be the primary key?
In the table above stu_name and course together form the Primary key because using stu_name and course, we can find all the columns of the table.
Also, one professor teaches only one course, but one course may have two different professors as we can see in the above table.
Hence, there is a dependency between course and professor, where the course depends on the professor's name.
The candidate key will be: {Stu_name, Course}.
Functional dependencies in the table above:
✍️ Stu_name, course -> Professor (Stu_name and course together determine the professor).
✍️ Professor -> course (Here professor determines the course since a subject can be taught by more than one professor).
Now to check whether the table is in BCNF we must check it is satisfying all the rules stated above.
First, we’ll start from 1NF: As we can see all the attributes have atomic values hence it is in 1NF.
Moving to 2NF: There must not exist any partial dependencies for a table to be in 2NF.
✍️ Stu_name, course -> Professor (Professor is fully dependent on the primary key hence there is no partial dependency in the first FD).
✍️ Professor -> course (Course is the prime attribute, hence no partial dependency).
Moving to 3NF: There must not exist any transitive dependencies for a table to be in 3NF or the determinant should either be a super key or the dependent is a prime attribute.
✍️ Stu_name, course -> Professor (The determinant is the super key hence satisfying the 3NF conditions).
✍️ Professor -> course (Course being the prime attribute satisfies the condition for 3NF).
From the above discussion, we can say that the table is in 3NF which is the first rule of BCNF. Yet the table isn’t in BCNF.
Now, what’s the problem here in the above table? The first functional dependency is valid as per the BCNF but the second is violating the condition. The course is a prime attribute determined by the non-prime attribute is the problem here.
Also, there are certain anomalies that can occur here like Insertion and Deletion anomalies.
😵 Insertion Anomaly: Suppose any new professor arrives and his/her data needs to be added to the table. Since the primary key cannot be null there must be any student who has to enrol in the course for that particular professor. This means that if there is no student right now enrolling for the course taught by the new professor, the professor data can’t be added.
😵 Deletion Anomaly: If any student wants to leave the course, the respected professor will also be removed.
To overcome such issues BCNF differentiates from the 3NF.
Now let us see how to convert this table into BCNF: