Solution Approach - As given in the CLRS book, using vectors and queue 💡

Now, let us talk about the solution approach given in the CLRS book. In this approach, a vector(g) stores the adjacency list of the graph, and the queue is used to keep track of the upcoming vertices in BFS order. Also, we would use two more vectors, one to keep track of the parent vertex for each vertex and the other to store the distance of a vertex from the source. We use the concept of coloring each vertex to keep track of whether the vertex is unvisited(white), partially visited(gray), or fully visited(black).
Let us now talk about the algorithm for the solution approach:
BFS(G, source)
-
For each vertex u, perform the following:
- Set colour[u] = WHITE
- distance[u] = infinity
-
parent[u] = None
- colour[source] = GRAY
- distance[source] = 0
- queue = NULL
-
Enqueue source to the queue
-
Perform the following while the queue is not empty,:
- Dequeue from the queue into u
-
For each v in the G[u]:
-
If colour[v] is WHITE, perform:
- set colour[v] = GRAY
- distance[v] = distance[u] + 1
- parent[v] = u
-
Enqueue v to the queue
- colour[u] = BLACK
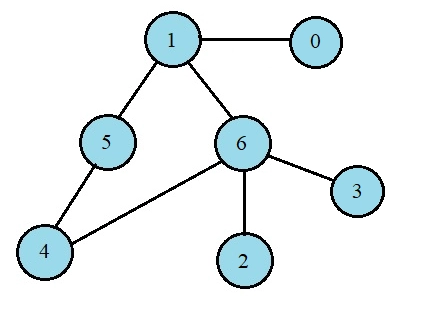
Lets us again discuss the algorithm with an example. Suppose you are given the below graph:
Then the BFS is performed in the below-given steps:
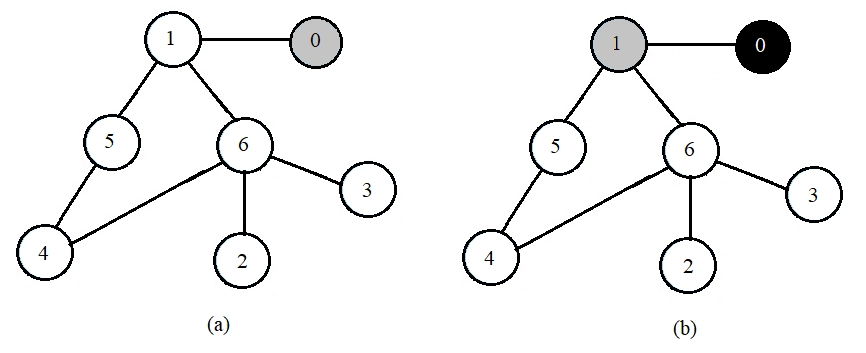
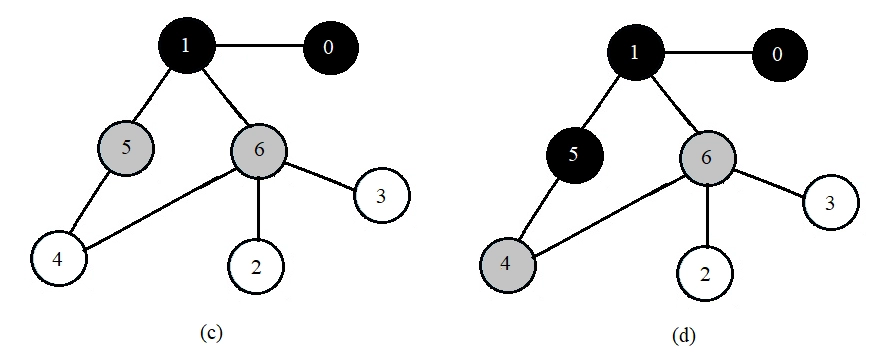
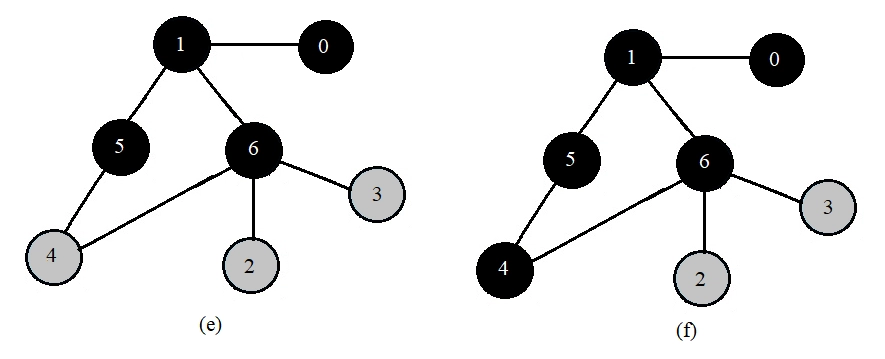
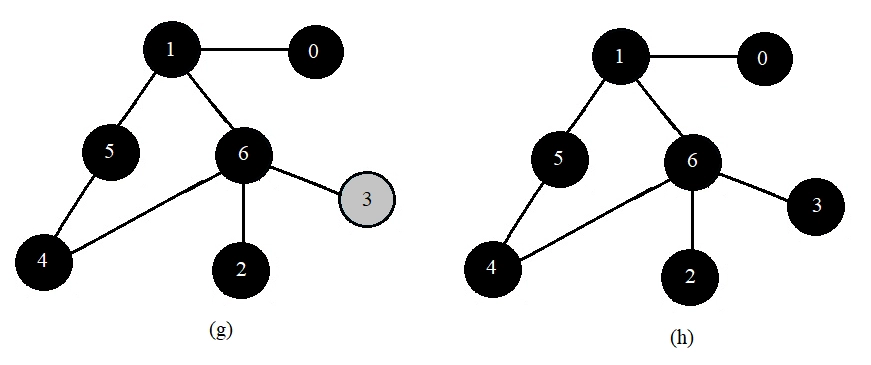
Now that we are clear with the approach, let us implement the algorithm in different languages for the above graph(Example above).
Python Implementation 📌
from queue import Queue
'''This is a utility function used to add an edge to your graph'''
def Edge(g,v1,v2):
g[v1].append(v2)
'''Considering it to be an undirected graph, and hence adding both the forward and backward edge'''
g[v2].append(v1)
'''The BFS function using approach given in the CLRS book'''
def BFS_CLRS(G, s, n):
'''Initializing vectors and queue'''
colour = ["white"] * n
distance = [10000000] * n
parent = [-1] * n
'''Setting values for the source vertex'''
colour[s] = 'gray'
distance[s] = 0
'''Initializing queue'''
q = Queue()
q.put(s)
'''Traversing While queue is not empty'''
while(not q.empty()):
u = q.get()
'''Printing the current vertex'''
print(u, end = ' ')
'''Adding the unvisited adjacent vertices of u to the queue'''
for v in G[u]:
if colour[v] == 'white':
colour[v] = 'gray'
distance[v] = distance[u] + 1
parent[v] = u
q.put(v)
'''Specifying that u is completely visited by setting its colour to black'''
colour[u] = 'black'
'''Driver Function'''
def main():
'''setting number of vertices to n'''
n = 7
'''The graph vector to store the adjacency list'''
G = [[] for i in range(n)]
'''Adding edges in the adjacency list'''
Edge(G, 0, 1)
Edge(G, 1, 5)
Edge(G, 1, 6)
Edge(G, 5, 4)
Edge(G, 6, 4)
Edge(G, 2, 6)
Edge(G, 3, 6)
'''Calling the BFS function'''
BFS_CLRS(G, 0, n)
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
Output 📄
0 1 5 6 4 2 3
C++ implementation 📌
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
/*This is a utility function used to add an edge to your graph*/
void Edge(vector <int> G[], int v1, int v2)
{
/*Considering it to be an undirected graph, and hence adding both the forward and backward edge*/
G[v1].push_back(v2);
G[v2].push_back(v1);
}
/*The BFS function using the approach given in the CLRS book*/
void BFS_CLRS(vector <int> G[], int source, int n)
{
/*Initializing vectors and queue*/
vector<string> colour(n, "white");
vector<int> distance(n, 1000000);
vector<int> parent(n, -1);
/*Setting values for the source vertex*/
colour[source] = "gray";
distance[source] = 0;
/*Initializing queue*/
queue<int> q;
q.push(source);
/*Traversing While queue is not empty*/
while (!q.empty())
{
/*pop out the front vertex from the queue*/
int u = q.front();
q.pop();
/*Printing the current vertex*/
cout<<u<<" ";
/*Adding the unvisited adjacent vertices of u to the queue*/
for (auto v = G[u].begin(); v != G[u].end(); v++)
{
if (colour[*v] == "white")
{
colour[*v] = "green";
distance[*v] = distance[u] + 1;
parent[*v] = u;
q.push(*v);
}
}
/*Specifying that u is completely visited by setting its colour to black*/
colour[u] = "black";
}
}
/*Driver Function*/
int main()
{
/*setting the number of vertices to n*/
int n = 7;
/*The graph vector to store the adjacency list*/
vector <int> G[n];
/*Adding edges in the adjacency list*/
Edge(G, 0, 1);
Edge(G, 1, 5);
Edge(G, 1, 6);
Edge(G, 5, 4);
Edge(G, 6, 4);
Edge(G, 2, 6);
Edge(G, 3, 6);
/*Calling the BFS function*/
BFS_CLRS(G, 0, n);
return 0;
}

You can also try this code with Online C++ Compiler
Output 📄
0 1 5 6 4 2 3
Complexities ⏳📂
The time complexity of the above approach is O(V + E), where V and E represent the number of vertices and edges, respectively.
The auxiliary space complexity of the above program is O(V), where V is total number of vertices.
Check out this problem - Queue Implementation
Frequently Asked Questions ❔
Does BFS also work with disconnected graphs?
The conventional/straightforward BFS approach does not work with the disconnected graphs as not all the vertices are connected with all the other vertices. But, with a modification in the simple approach, you can make BFS work for disconnected graphs too.
What is the time complexity of the BFS algorithm?
The time complexity of the BFS algorithm is the same for both connected and disconnected graphs and is equal to O(number_of_vertices + number_of_edges).
What is the auxiliary space complexity of the BFS algorithm? and why?
The auxiliary space complexity of the BFS algorithm is O(V), where V is the number of vertices. The additional space is required to store the vertices in the visited array and the queue.
How many times is a vertex visited in BFS?
In the BFS algorithm, each vertex is visited mandatorily and only once. No vertex is visited twice or more. A Boolean Visited array is used to keep track and make sure you visit each vertex only once.
What is a disconnected graph?
In a disconnected graph, all the vertices are not connected with all the other vertices(directly or indirectly). It is created by two or more connected graphs being unconnected but part of a single disconnected graph.
Conclusion
This article discussed the method to perform BFS using vectors and queues as per the algorithm given in the CLRS book.
To learn more about BFS in Connected graph, visit Breadth-First Search. And to learn more about BFS in a disconnected graph, visit BFS in a disconnected graph.
I hope you would have gained a better understanding of these topics now!
Are you planning to ace the interviews with reputed product-based companies like Amazon, Google, Microsoft, and more?
Attempt our Online Mock Test Series on Coding Ninjas Studio now!
Happy Coding!