Introduction
A binary tree is a tree Data Structure where every node has a maximum of two children (could be 0, 1, 2), referred to as the left child and the right child.
BFS (Breadth-First Search) and DFS (Depth-First Search) are tree traversal algorithms. In BFS, we start with the root node and then traverse the tree row by row, and in DFS, we begin with the root node and traverse the tree in depth until we find the node with no children and backtrack it.
BFS
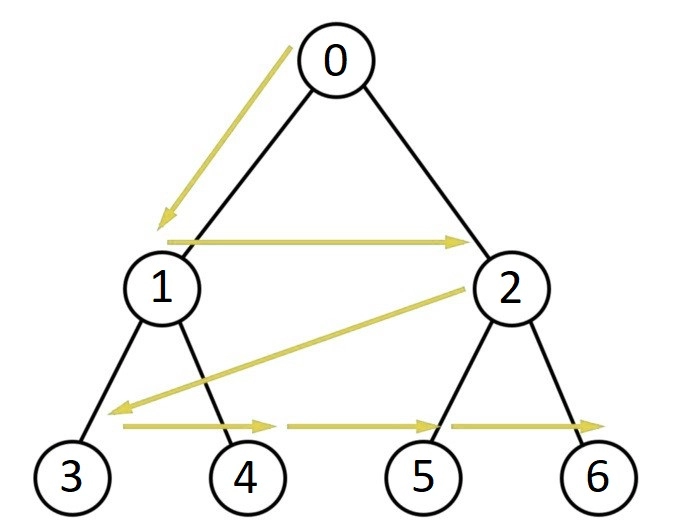
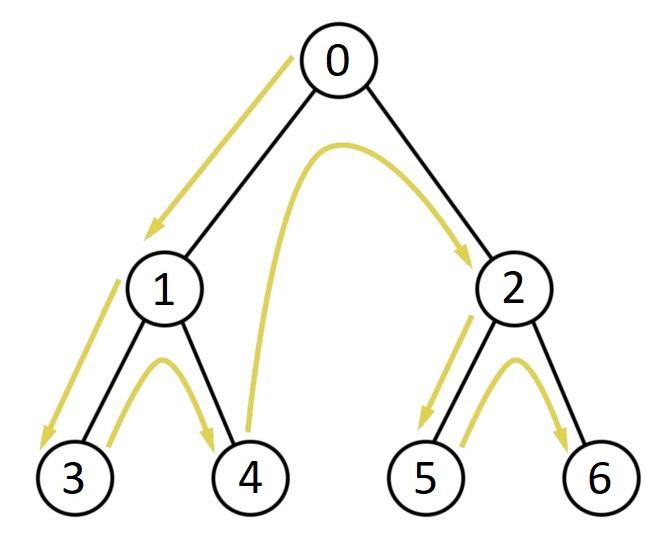
Breadth-First Search is also known as Level Order Traversal. This algorithm starts with the root node and then visits all nodes level by level from left to right. Here we see every node on a level before going to a lower level. To implement BFS, we use a queue. The Breadth-First Search for trees can be implemented using level order traversal.
Algorithm
Let us look at the algorithm to implement BFS.
- Start from root
- Insert the root node into BFS and all of that node's neighbours into the queue.
- If the node is not visited, pop it from the queue and add it to BFS, as well as all of its unvisited neighbours.
- Repeat until the queue's size is not equal to zero(NULL).
Example
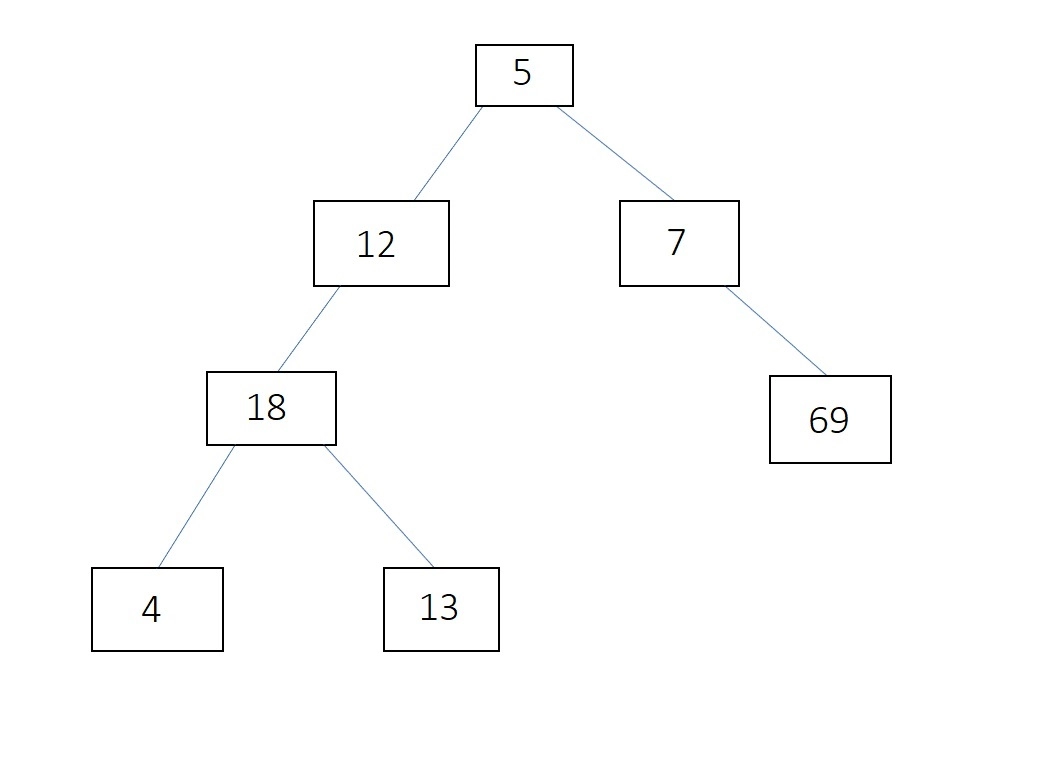
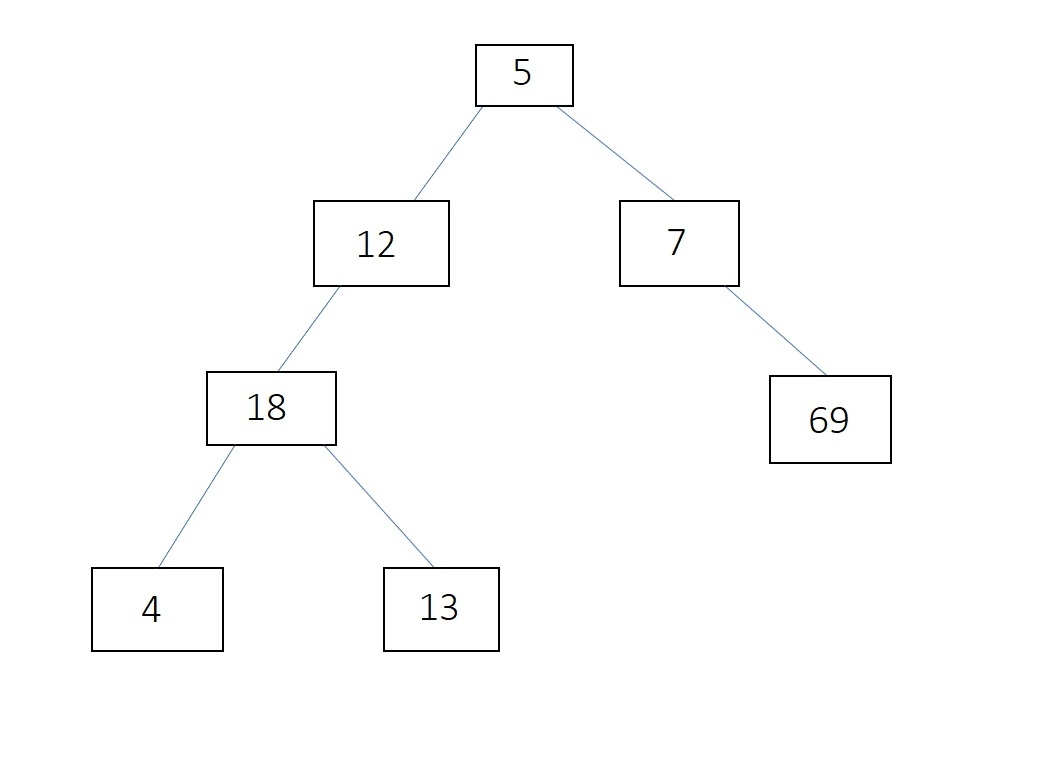
BFS Implementation
#include <iostream>
#include <queue>
using namespace std;
// Structure for holding data, references to the left child and the right child of the current node
struct node {
int data;
struct node *left, *right;
};
// Method for initialising new node with provided data value
node* new_node(int data) {
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main() {
node *root = new_node(5);
root->left = new_node(12);
root->right = new_node(7);
root->left->left = new_node(18);
root->left->left->left = new_node(4);
root->left->left->right = new_node(13);
root->right->right = new_node(69);
cout << "BFS for the above tree will be: \n";
// We will use a queue data structure for maintaining order between nodes
queue<node *> q;
// Pushing the root node into the queue
q.push(root);
// Iterating over the queue until its non empty
while (q.empty() == false){
// Printing the current node from front of the queue
node *node = q.front();
cout << node->data << " ";
// Removing the front node
q.pop();
// Pushing left and right child into the queue only if they exist
// We push the left child first so as to maintain the order
if (node->left != NULL)
q.push(node->left);
if (node->right != NULL)
q.push(node->right);
}
return 0;
}
Output
BFS for the above tree will be:
5 12 7 18 69 4 13
Time Complexity
Time complexity is the order of n, i.e., O(n), where n is the number of nodes in the tree (each node is visited exactly once).
Must Read Algorithm Types