Biconnected Components in Graph

Introduction 🚀

Hey Ninja!! You have come pretty far reading graphs 🧑‍💻. In the domain of computer science, we always want to build robust systems and make sure that there is no point of failure. Therefore we take extra precautions to make our system fault-proof. Having knowledge of articulation points and biconnected components reduces our risk. 

This article will discuss how to find biconnected components in graphs. We will learn how to apply the idea of articulation points to come up with an algorithm to find biconnected components. 

Problem Statement

Given a graph with V vertices and E edges, your task is to print all the biconnected components present in the graph.
 

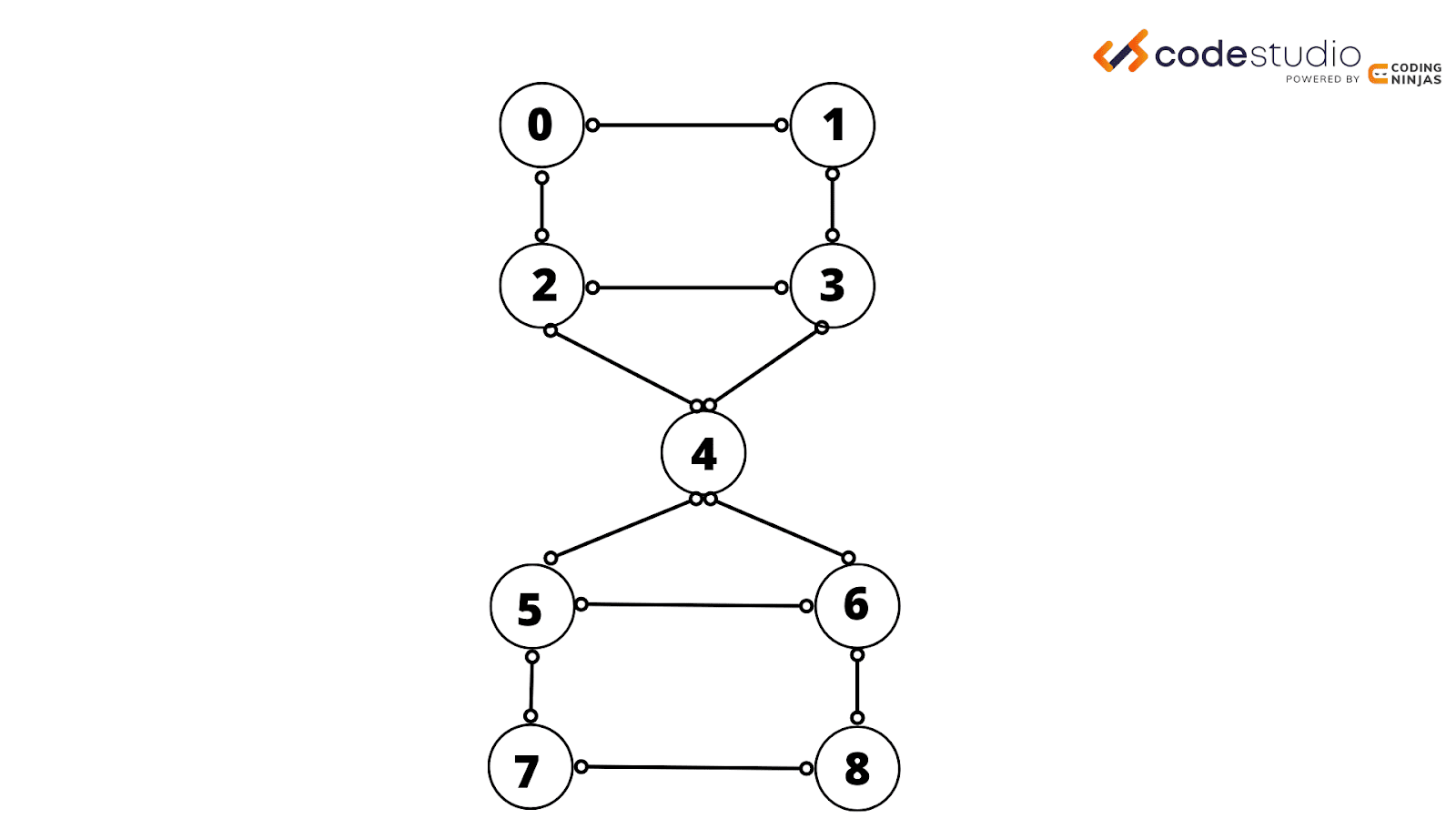
For example, look at the graph below:

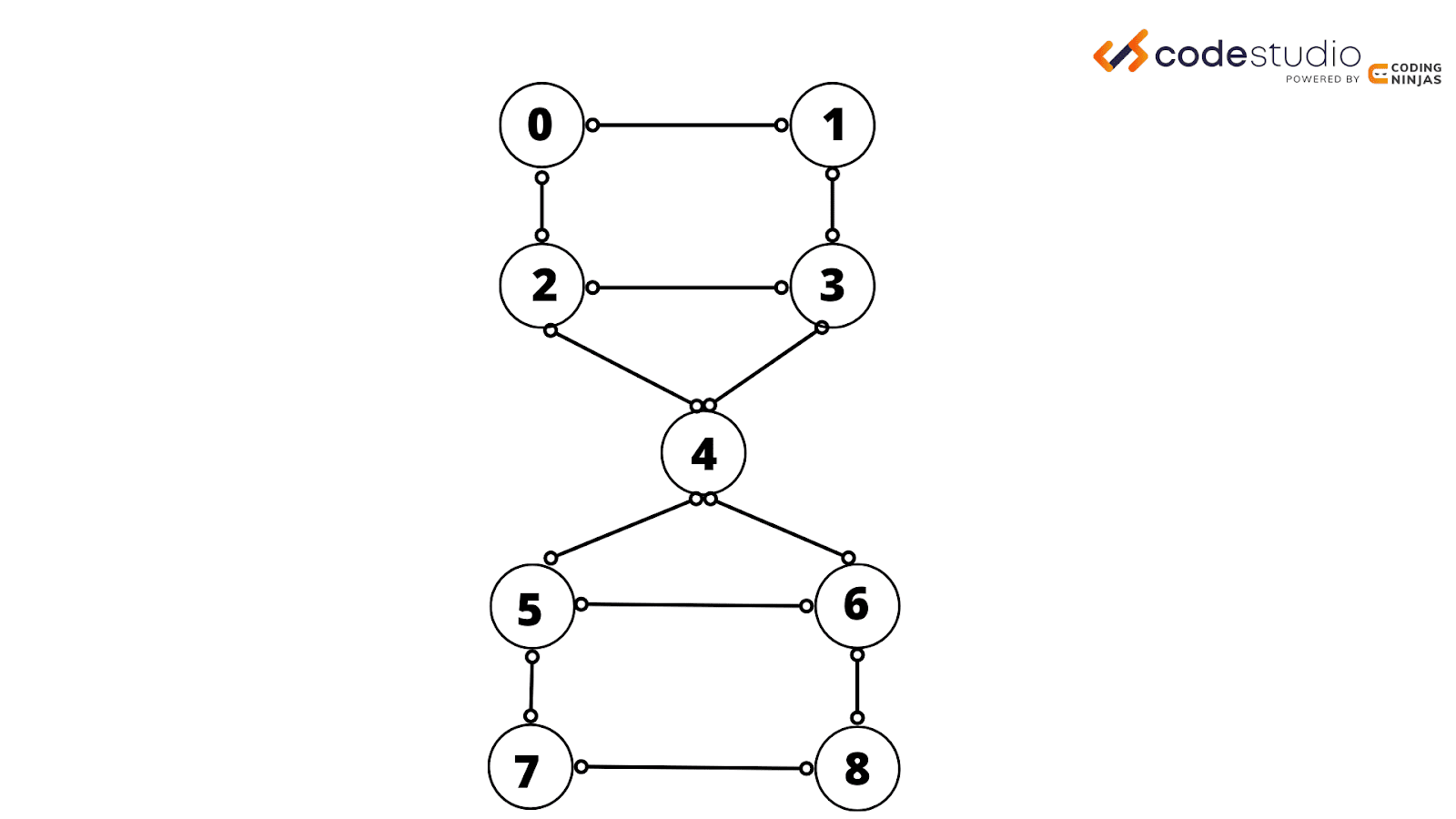
The output for the above graph should be :
 

7–5  8–7 6–8 6–4 5–6 4–5
4–3 2–4 2–0 3–2 1–3 0–1  

Articulation Points

An articulation point is a node in a graph that, when removed, divides the graph into two or more components.

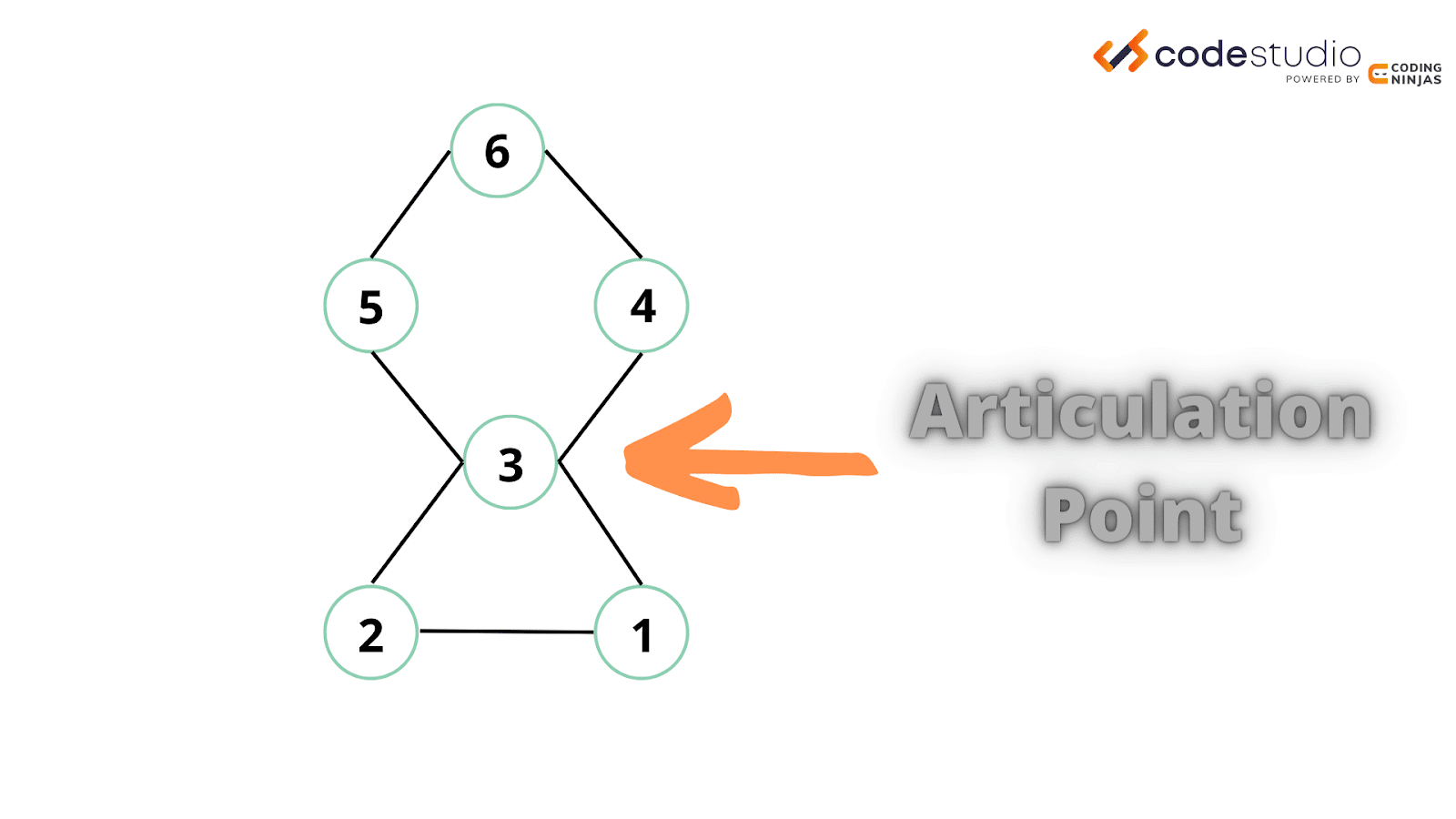
In the above image, the node with value ‘3’ is an articulation point because its removal will break the graph into three separate components.

Biconnected Graph

For any graph to qualify as a biconnected graph, it must satisfy the following constraints:

• Connected Graph: It means that it is possible to reach any node starting from any random node, i.e. there are no two components without an edge between them.
• No articulation points: The existence of articulation points makes the graph not biconnected.
   

Biconnected Components 💡

A biconnected component is a subgraph which always has a path between two nodes in the component even after removing a node.

For example, the image below shows a graph with two biconnected components:

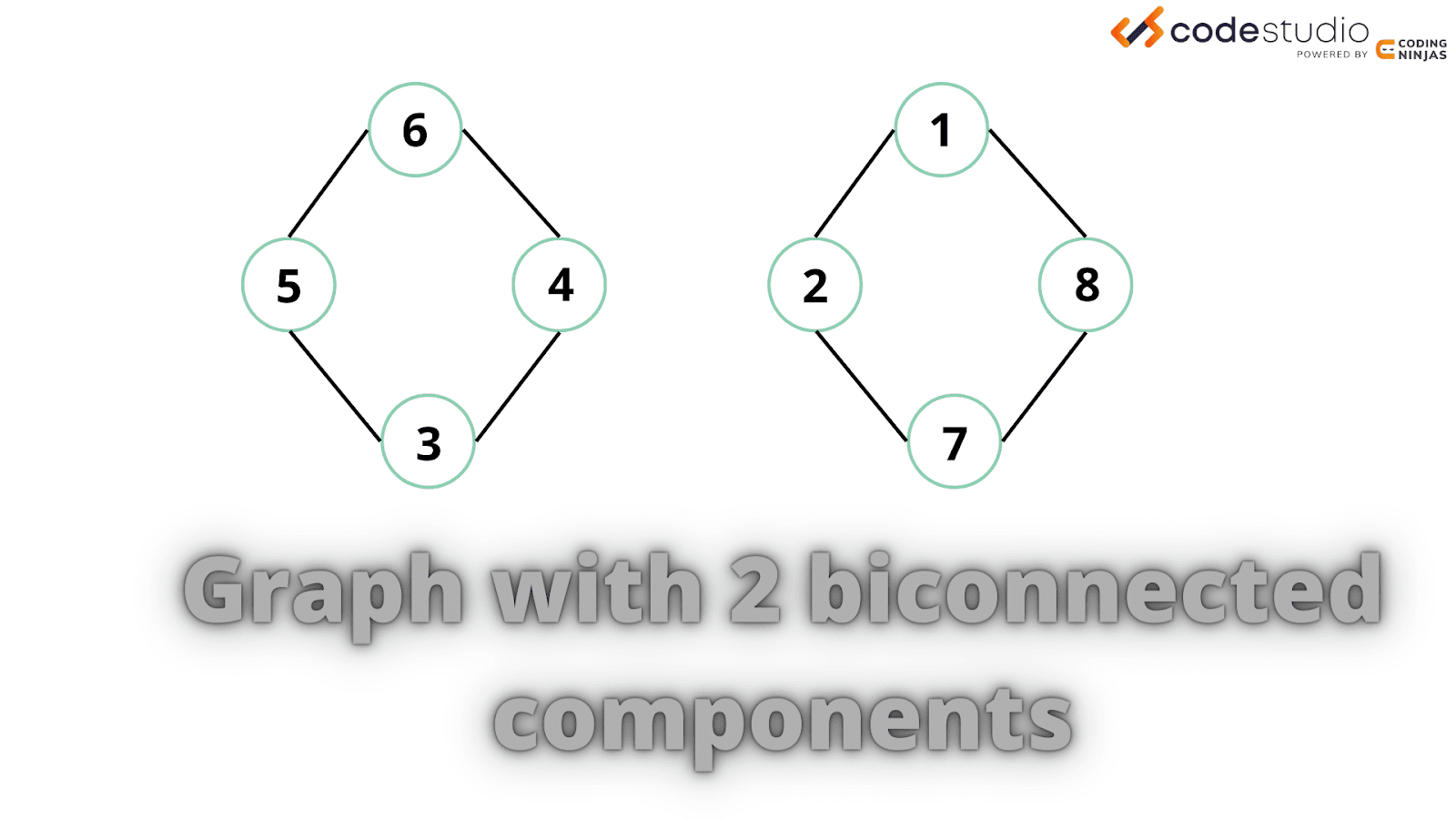
Biconnected components can be determined with an algorithm similar to that of finding articulation points. We will go through the algorithm in the section below. 😁
 

Algorithm🤖

Let us go through the steps needed to find biconnected components :

• Initialise an empty stack to store edges.
• Run a DFS and look for articulation points.
• At each node, keep track of low values and discovery time.
• If an articulation point is found, all the edges visited from this point onwards will form the biconnected component.
• If there are no articulation points, then the entire graph is one single biconnected component.

Code Implementation🗒️

In this section, we will walk through the code implementation in C++. Proper comments are added for ease of understanding:

#include<bits/stdc++.h>
using namespace std;


//graph structure definition
class Graph {
    int Vertices; // vertices count
    int Edges; //number of edges
    vector<int>* adj; //adjacency list
 
   // private helper function to run the dfs
    void helper(int u, vector<int>&discoveryTime, vector<int>&low,
                 stack<pair<int,int>> &stackk, vector<int>&parent){
                     static int time = 0;
 
    discoveryTime[u] = low[u] = ++time;
    int children = 0;
 
        for(auto v:adj[u]){
            
        if (discoveryTime[v] == -1) {
            children++;
            parent[v] = u;
          
            stackk.push({u,v});
            helper(v, discoveryTime, low, stackk, parent);
 
            low[u] = min(low[u], low[v]);
 
            
            if ((discoveryTime[u] == 1 && children > 1) || (discoveryTime[u] > 1 && low[v] >= discoveryTime[u])) {
                while (stackk.top().first != u || stackk.top().second != v) {
                    cout << stackk.top().first << "--" << stackk.top().second << " ";
                    stackk.pop();
                }
                cout << stackk.top().first << "--" << stackk.top().second;
                stackk.pop();
                cout << endl;
            }
        }
 
        else if (v != parent[u]) {
            low[u] = min(low[u], discoveryTime[v]);
            if (discoveryTime[v] < discoveryTime[u]) {
                stackk.push({u,v});
            }
        }
    }
                 }
 
public:
    //constructor to initialise members of the class
    Graph(int V){
        Vertices=V;
        Edges=0;
        adj = new vector<int>[V];
    }
 
    void addEdge(int a, int b){
    adj[a].push_back(b);
    adj[b].push_back(a);
    Edges++;
    } 


   //Function to print biconnected components
    void biconnectedComponents(){
    vector<int>discoveryTime(Vertices,-1);
    vector<int>low(Vertices,-1);
    vector<int>parent(Vertices,-1);
    
    stack<pair<int,int>> stackk;
    for (int i = 0; i < Vertices; i++) {
        if (discoveryTime[i] == -1)
            helper(i, discoveryTime, low, stackk, parent);
 


        while (stackk.size() > 0) {
            cout << stackk.top().first << "--" << stackk.top().second << " ";
            stackk.pop();
        }
        cout<<endl;
    }
    }
};


//main function definition
int main()
{
    Graph g(9);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 3);
    g.addEdge(2, 3);
    g.addEdge(2, 4);
    g.addEdge(3, 4);
    g.addEdge(4, 5);
    g.addEdge(4, 6);
    g.addEdge(5, 6);
    g.addEdge(5, 7);
    g.addEdge(6, 8);
    g.addEdge(7,8);
    g.biconnectedComponents();
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input Visualisation :

Output:

Time complexity

The time complexity of the above logic is O(V+E). The code runs a simple depth search that goes to each and every element in the adjacency list. Therefore the complexity is O(V+E).
 

Space Complexity

Since, in one instance, all the edges can be in a stack of edges, the space complexity is  O(V).