Introduction
To understand the working of Bi-LSTM first, we need to understand the unit cell of LSTM and LSTM network. LSTM stands for long short-term memory. In 1977 Hochretier and Schmidhuber introduced LSTM networks. These are the most commonly used recurrent neural networks.
Need of LSTM
As we know that sequential data is better handled by recurrent neural networks, but sometimes it is also necessary to store the result of the previous data. For example, “I will play cricket” and “I can play cricket” are two different sentences with different meanings. As we can see, the meaning of the sentence depends on a single word so, it is necessary to store the data of previous words. But no such memory is available in simple RNN. To solve this problem, we need to study a term called LSTM.
Also Read, Resnet 50 Architecture
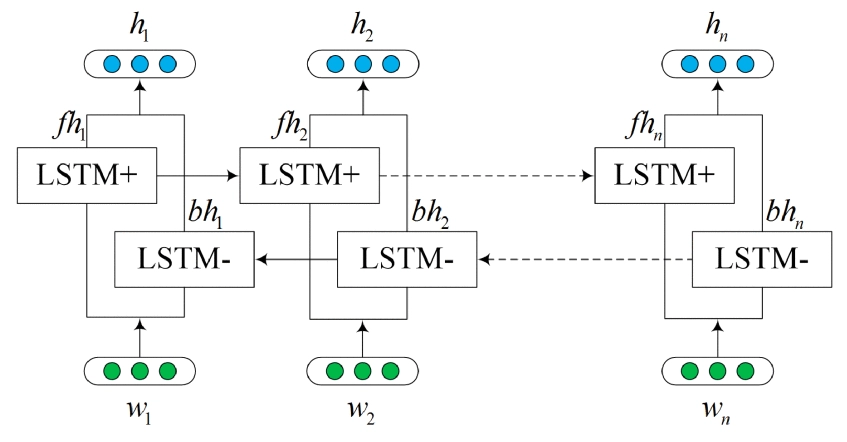
The Architecture of the LSTM Unit
The image below is the architecture of the LSTM unit.

The LSTM unit has three gates:
Input gate
First, the current state x(t) and previous hidden state h(t-1) are passed into the input gate, i.e., the second sigmoid function. The x(t) and h(t-1) values are transformed between 0 and 1, where 0 is important, and 1 is not important. Furthermore, the current and hidden state information will be passed through the tanh function. The output from the tanh function will range from -1 to 1, and it will help to regulate the network. The output values generated from the activation functions are ready for point-by-point multiplication.
Forget gate
The forget gate decides which information needs to be kept for further processing and which can be ignored. The hidden state h(t-1) and current input X(t) information are passed through the sigmoid function. After passing the values through the sigmoid function, it generates values between 0 and 1 that conclude whether the part of the previous output is necessary (by giving the output closer to 1).
Output gate
The output gate helps in deciding the value of the next hidden state. This state contains information on previous inputs. First, the current and previously hidden state values are passed into the third sigmoid function. Then the new cell state generated from the cell state is passed through the tanh function. Both these outputs are multiplied point-by-point. Based upon the final value, the network decides which information the hidden state should carry. This hidden state is used for prediction.
Finally, the new cell state and the new hidden state are carried over to the next step.
To conclude, the forget gate determines which relevant information from the prior steps is needed. The input gate decides what relevant information can be added from the current step, and the output gates finalize the next hidden state.