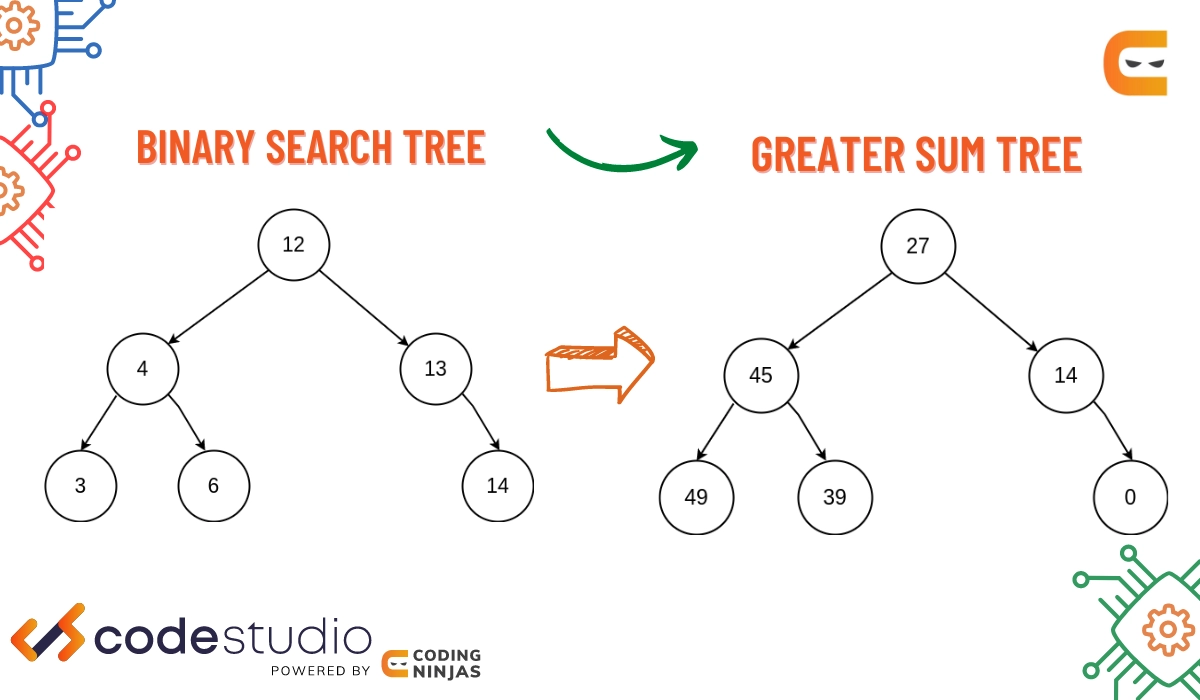
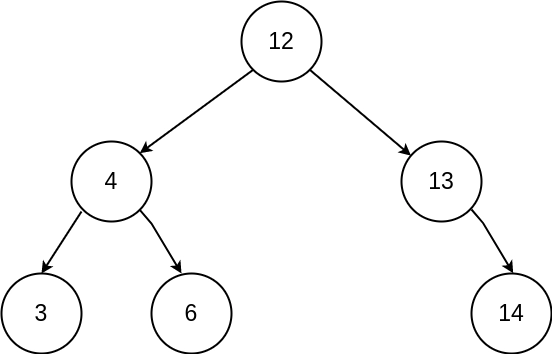
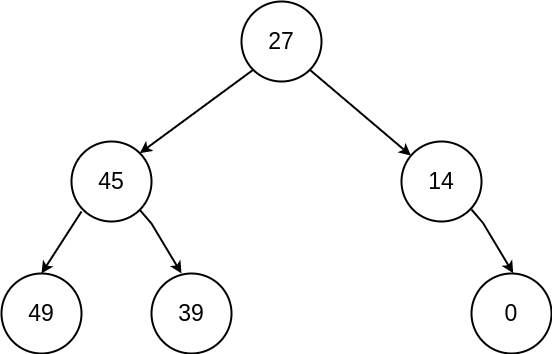
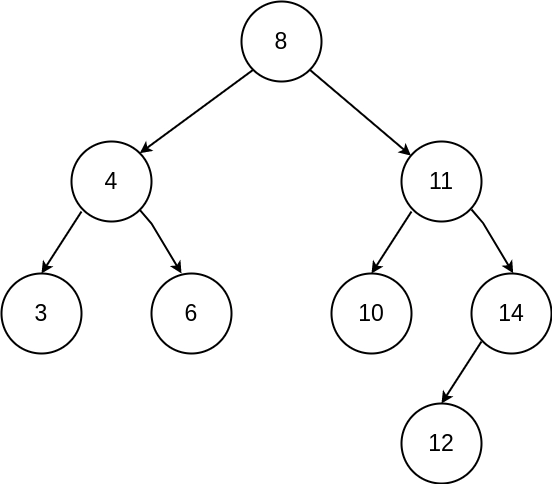
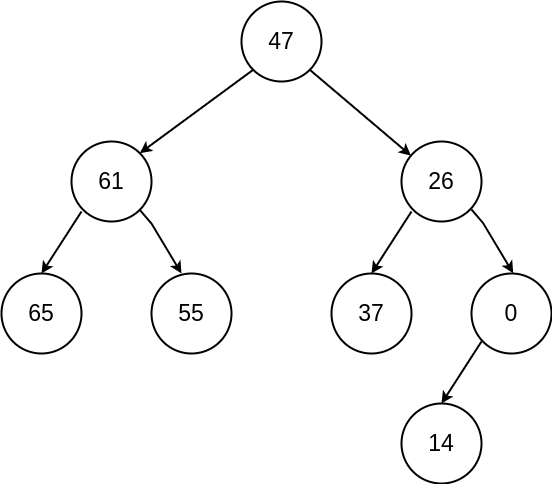
Approach #1
A straightforward approach to solve this problem is traverse the given binary search tree and for each node:
-
Determine the sum of all those nodes’ values which are greater than the node.
- Replace the node’s value with the sum obtained in the previous step.
Algorithm
-
Initialize the root as NULL.
-
For each node in the BST:
-
Traverse the given BST using either inorder, preorder or postorder traversals.
-
Now, find the sum of all those nodes which are greater than the node.
-
Finally, update the value of the node in the BST data structures.
- Display preorder traversal of the new BST thus created.
Implementation in C++
// C++ Program to find greater sum tree
#include <bits/stdc++.h>
using namespace std;
// A node in the BST
struct Node
{
int val;
Node *left, *right;
};
// Function to create nodes in the BST
Node *createNode(int val)
{
// Create the node
Node *node = new Node();
// Assign the value
node->val = val;
// Assign left and right pointers as null
node->left = NULL;
node->right = NULL;
// Return the node.
return node;
}
// Function to find the sum of nodes greater than val
int findGreaterSum(Node *root, int val)
{
if (root == NULL)
return 0;
// Iterate the left and right subtree and get the desired sum
int leftSum = findGreaterSum(root->left, val);
int rightSum = findGreaterSum(root->right, val);
// If the node is greater than val, include it's value in the sum
int ans = leftSum + rightSum;
if (root->val > val)
ans += root->val;
return ans;
}
// Function to generate the greater sums for all nodes
void generateGreaterSums(Node *node, Node *root, vector<int> &storeSums)
{
if (node == NULL)
return;
// Calculate the sum
int sum = findGreaterSum(root, node->val);
// Store the greater sums
storeSums.push_back(sum);
// Do the same for other nodes.
generateGreaterSums(node->left, root, storeSums);
generateGreaterSums(node->right, root, storeSums);
}
// Function to assign the greater sums generated from the previous function
// to the nodes
void assignGreaterSums(Node *root, int &i, vector<int> &greaterSums)
{
if (root == NULL)
return;
// Update the value of the node
root->val = greaterSums[i++];
// Do the same for left and right subtrees
assignGreaterSums(root->left, i, greaterSums);
assignGreaterSums(root->right, i, greaterSums);
}
// Utility function to generate the Greater Sum Tree
void generateGreaterSumTree(Node *root)
{
// To store the greater sums for all nodes
vector<int> greaterSums;
Node* newRoot = root;
// Find the greater sums for all nodes
// and store them in greaterSums
generateGreaterSums(newRoot, newRoot, greaterSums);
// Now assign the greater sums
int ind = 0;
assignGreaterSums(root, ind, greaterSums);
}
// Standard function for inorder traversal
void inorderTraversal(Node *root)
{
if (root == NULL)
return;
inorderTraversal(root->left);
cout << root->val << " ";
inorderTraversal(root->right);
}
// Standard function for preorder traversal
void preorderTraversal(Node *root)
{
if (root == NULL)
return;
cout << root->val << " ";
preorderTraversal(root->left);
preorderTraversal(root->right);
}
int main()
{
// Create the BST
struct Node *root = createNode(8);
root->left = createNode(4);
root->right = createNode(11);
root->left->left = createNode(3);
root->left->right = createNode(6);
root->right->left = createNode(10);
root->right->right = createNode(14);
root->right->right->left = createNode(12);
// Inorder traversal of the input tree
cout << "Inorder traversal of the given tree:\n";
inorderTraversal(root);
// Create greater sum tree
generateGreaterSumTree(root);
// Inorder and preorder traversals of the greater sum tree
cout << "\n\nInorder traversal of the greater sum tree:\n";
inorderTraversal(root);
cout << "\nPreorder traversal of the greater sum tree:\n";
preorderTraversal(root);
return 0;
}

You can also try this code with Online C++ Compiler
Output
Inorder traversal of the given tree:
3 4 6 8 10 11 12 14
Inorder traversal of the greater sum tree:
65 61 55 47 37 26 14 0
Preorder traversal of the greater sum tree:
47 61 65 55 26 37 0 14
Time Complexity Analysis
The time complexity of the above approach is O(N * N) where N is the number of nodes in the tree. It is because for each node, we are traversing the whole BST to find the sum of nodes greater than the current node.
Space Complexity Analysis
The space complexity of the above program is O(N), where N is the number of nodes in the BST. It is because we are storing the greater sums in a vector whose size will go upto N.
Approach #2
This approach is based on reverse inorder traversal of a BST. We know that inorder traversal of a BST gives a sorted sequence. However, if we perform reverse inorder traversal, we will get a decreasing sequence.
So we can perform the reverse inorder traversal of a BST and keep adding the node values. Before arriving at a node, we have already encountered - all those nodes greater than the current node. Hence we just need to update the node’s value in the BST to the sum collected so far.
Algorithm
-
Initialize the root as NULL and sum = 0
-
Perform postorder traversal on the input BST and update the sum variable as sum += node’s value.
-
For each node encountered, just update its value to the value of sum so far.
- The sum variable should not include the current node’s value.
Implementation in C++
// C++ Program to find greater sum tree
#include <bits/stdc++.h>
using namespace std;
// A node in the BST
struct Node
{
int val;
Node *left, *right;
};
// Function to create nodes in the BST
Node *createNode(int val)
{
// Create the node
Node *node = new Node();
// Assign the value
node->val = val;
// Assign left and right pointers as null
node->left = NULL;
node->right = NULL;
// Return the node.
return node;
}
// Utility function to generate the Greater Sum Tree
void generateGreaterSumTree(Node *root, int &sumTillNow)
{
if (root == NULL)
return;
// Reverse Inorder Traversal
// Right subtree
generateGreaterSumTree(root->right, sumTillNow);
// Preserve the current node value
int currVal = root->val;
// Update the tree
// as all nodes with values greater than the current node
// have been added to sumTillNow
root->val = sumTillNow;
// Add the current node
sumTillNow += currVal;
// Finally for left
generateGreaterSumTree(root->left, sumTillNow);
}
// Standard function for inorder traversal
void inorderTraversal(Node *root)
{
if (root == NULL)
return;
inorderTraversal(root->left);
cout << root->val << " ";
inorderTraversal(root->right);
}
// Standard function for preorder traversal
void preorderTraversal(Node *root)
{
if (root == NULL)
return;
cout << root->val << " ";
preorderTraversal(root->left);
preorderTraversal(root->right);
}
int main()
{
// Create the BST
struct Node *root = createNode(8);
root->left = createNode(4);
root->right = createNode(11);
root->left->left = createNode(3);
root->left->right = createNode(6);
root->right->left = createNode(10);
root->right->right = createNode(14);
root->right->right->left = createNode(12);
// Inorder traversal of the input tree
cout << "Inorder traversal of the given tree:\n";
inorderTraversal(root);
// Create greater sum tree
int sumTillNow = 0;
generateGreaterSumTree(root, sumTillNow);
// Inorder and preorder traversals of the greater sum tree
cout << "\n\nInorder traversal of the greater sum tree:\n";
inorderTraversal(root);
cout << "\nPreorder traversal of the greater sum tree:\n";
preorderTraversal(root);
return 0;
}

You can also try this code with Online C++ Compiler
Output
Inorder traversal of the given tree:
3 4 6 8 10 11 12 14
Inorder traversal of the greater sum tree:
65 61 55 47 37 26 14 0
Preorder traversal of the greater sum tree:
47 61 65 55 26 37 0 14
Time Complexity Analysis
The time complexity of the above approach is O(N ) where N is the number of nodes in the tree. It is because for each node, we are traversing the whole BST only once during reverse postorder traversal. And that’s it.
Space Complexity Analysis
The space complexity of the above program is O(H), where H is the height of the input BST. It is because we can go upto O(H) stack memory to call recursive functions.
You can also read about insertion into bst.
Frequently Asked Questions
What is a binary search tree?
Binary search trees are data structures that efficiently represent and perform certain tree operations, such as insertion, deletion, and searching. In a binary search tree, each node has values less than it to its left subtree and values greater than it on the right subtree.
What are the advantages of using Binary Search Trees?
Binary Search Trees perform important operations such as searching, deletion, insertion, etc. in less amount of time. For balanced binary search trees, these operations are deterministic - O(logN) time for most operations.
What is the time and space complexity of insertion in a binary search tree?
Space Complexity is O(1) and Insertion is O(logN) or O(N) depending on whether the tree is balanced or not.
Conclusion
The article explained two crucial topics in Data Structures and Algorithms - Binary Search Trees and Reverse Inorder Traversal. We discussed an approach involving reverse inorder traversal to solve the problem. This approach works out because the input is a BST. However, the first approach is universal in nature - It does not require the tree to be a BST.
If you think this blog has helped you enhance your knowledge about the above question, and if you would like to learn more, check out our articles
and many more on Coding Ninjas Studio.
Recommended problems -
Visit our website to read more such blogs. Make sure that you enroll in the courses provided by us, take mock tests and solve problems and interview puzzles available. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.
Please upvote our blog in case you find them interesting to help other ninjas grow.
Happy Learning!