Introduction
A Tree is a non-linear data structure that helps us hierarchically organize data. The non-linearity that comes with this Data Structure makes it feasible to solve complex problems. A Binary Tree is a special case of tree data structure that can have not more than two children.

This quick guide on Binary Tree Interview Questions will help a lot if you prepare for an interview regarding the same in the future. This article consists of the 30 most popular Binary Tree Interview Questions, so let’s get started without wasting time.
Binary Tree Interview Questions For Freshers
1. How can we define the depth or height of a Binary Tree?
The height or depth of a Binary Tree can be defined as the maximum number of nodes in a tree branch. We can also define the maximum number of nodes in a Binary Tree of depth ‘x’ as ‘2x - 1’. The depth of the root node is said to be one.
2. What are the applications of binary trees?
Some prominent applications of binary trees include
- High-bandwidth router for storing router tables.
- Algorithms for compression and many more.
- Search applications in which data is being left or entered constantly.
- Wireless networking.
- Memory allocation.
3. Explain the difference between full and perfect binary trees.
A full binary tree is one in which every node has exactly either 0 or 2 children.
A Binary Tree in which every internal node has two children and every leaf node is at the same level is called a perfect binary tree.
4. Give one example each explaining the Complete Binary Tree, Degenerate Tree, and Balance Binary Tree.
Complete Binary Tree
A complete binary tree is the one in which every level, maybe except for the final, must be filled. Also, all the other nodes must be as far to the left as feasible.
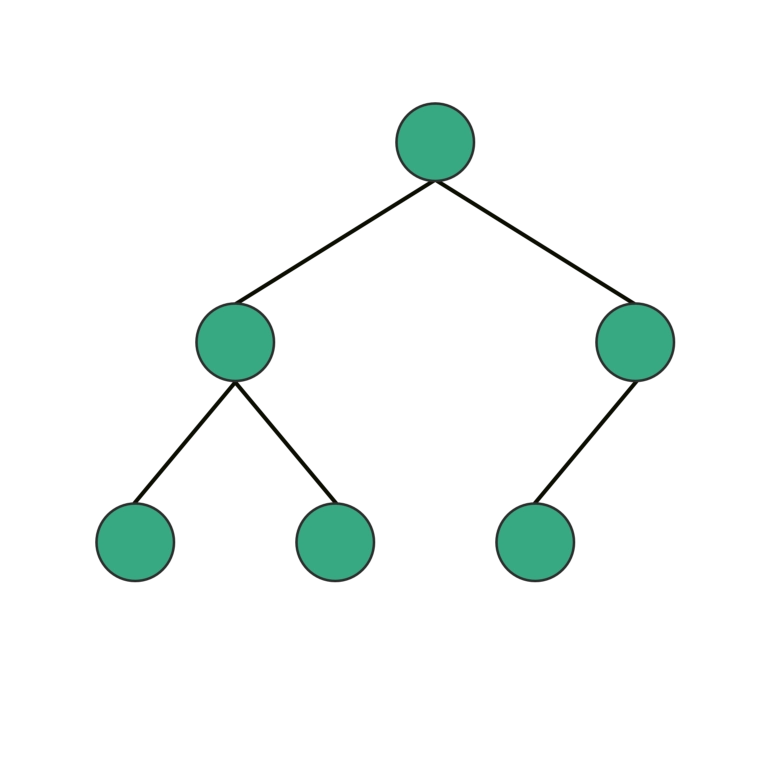
Balanced Binary tree
A type of Binary Tree in which the difference between left and right subtrees is not more than one.

Degenerate Tree
It is a binary tree in which every node has either zero or one parent.

7. Mention three cases that arise when you have found a node that you want to delete from Binary Tree.
Once you have found the node you want to delete, three prominent cases may arise.
- The node has no children.
You need to replace this node with null.
- The node has one child.
We will replace this node with its only child.
- The node has two children.
It requires a tree reorganization.
8. Are B-Trees the same as Binary Trees?
B-Trees are not binary trees because their nodes can have more than two children.
Search Trees designed especially for a huge amount of data, usually on a disk, are known as B-Trees. These are optimized to reduce the disk access operations for retrieving the node.
9. Define AVL Trees.
An AVL Tree is a height balancing binary search tree. The height balancing is done so that the difference between the height of the left and the right sub-trees should not exceed 1.
This difference is called the Balance Factor. It allows us to search for an element in the tree in O(log n) complexity.
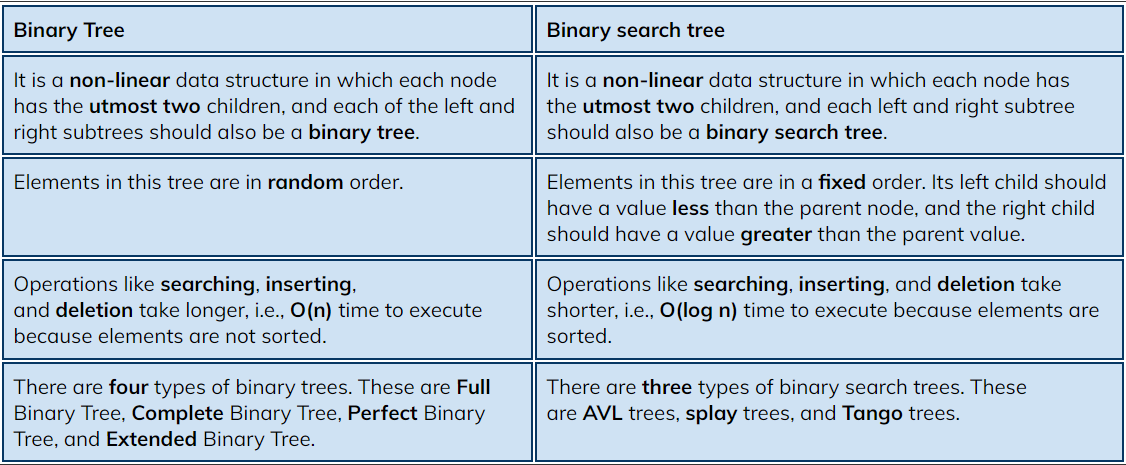
10. Mention differences between the Binary tree and the Binary search tree.
11. How to implement Breadth First Search in a Binary Tree?
In this traversal, the pointer visits all the nodes of that level before going to another level. We use the queue data structure for its implementation.
public void LevelOrder()
{
if (root == null)
return;
Queue<Node> nodes = new List<>();
nodes.add_node(root);
while (!nodes.isEmpty())
{
Node node = nodes.remove();
System.out.print(" " + node.value);
if (node.left != null)
nodes.add_node(node.left);
if (node.right != null)
nodes.add_node(node.right);
}
}12. What is Depth First Search? Give Pseudocodes explaining the ways to perform Depth First Search.
The type of traversal that goes deep into the node as possible and explores every child of it. Then, the pointer explores the next sibling of the currently visited node.
There are three ways to perform a depth-first search.
Inorder:
The left subtree, the root node, and the right subtree.
public void InOrder(Node node)
{
if (node != null) {
InOrder(node.left);
System.out.print(" " + node.value);
InOrder(node.right);
}
}
Pre-Order:
The root node, the left sub-tree, and the right sub-tree.
public void PreOrder(Node node)
{
if (node != null) {
System.out.print(" " + node.value);
PreOrder(node.left);
PreOrder(node.right);
}
}
Post-Order:
The left subtree, then the right sub-tree, and finally the root node
public void PostOrder(Node node)
{
if (node != null) {
PostOrder(node.left);
PostOrder(node.right);
System.out.print(" " + node.value);
}
}13. How would you search for an element in a Binary Tree?
- We will create a recursive method for traversing the tree.
- Now, we must search for the value by comparing it to the current node’s value.
- Continue moving to the left or right, depending upon the outcome.
The Pseudocode for the same is given below.
private boolean find(Node current, int val)
{
if (current == null)
return false;
if (val == current.val)
return true;
return val < current.val ? find(current.left, val) : find(current.right, val);
}
public boolean Node(int val)
{
return find(root, val);
}14. Explain the implementation of a Binary Heap.
A Binary Heap is a binary tree type that follows all the properties of a binary tree. Usually, a binary heap is implemented along with an array. As a Binary heap is always a complete binary tree, it can be stored compactly. No extra space is required for pointers. The parent and child nodes can be found using the arithmetic below.
- The root element is 0
- Left-child : (2*i)+1
- Right-child : (2*i)+2
- Parent-child : (i-1)/2
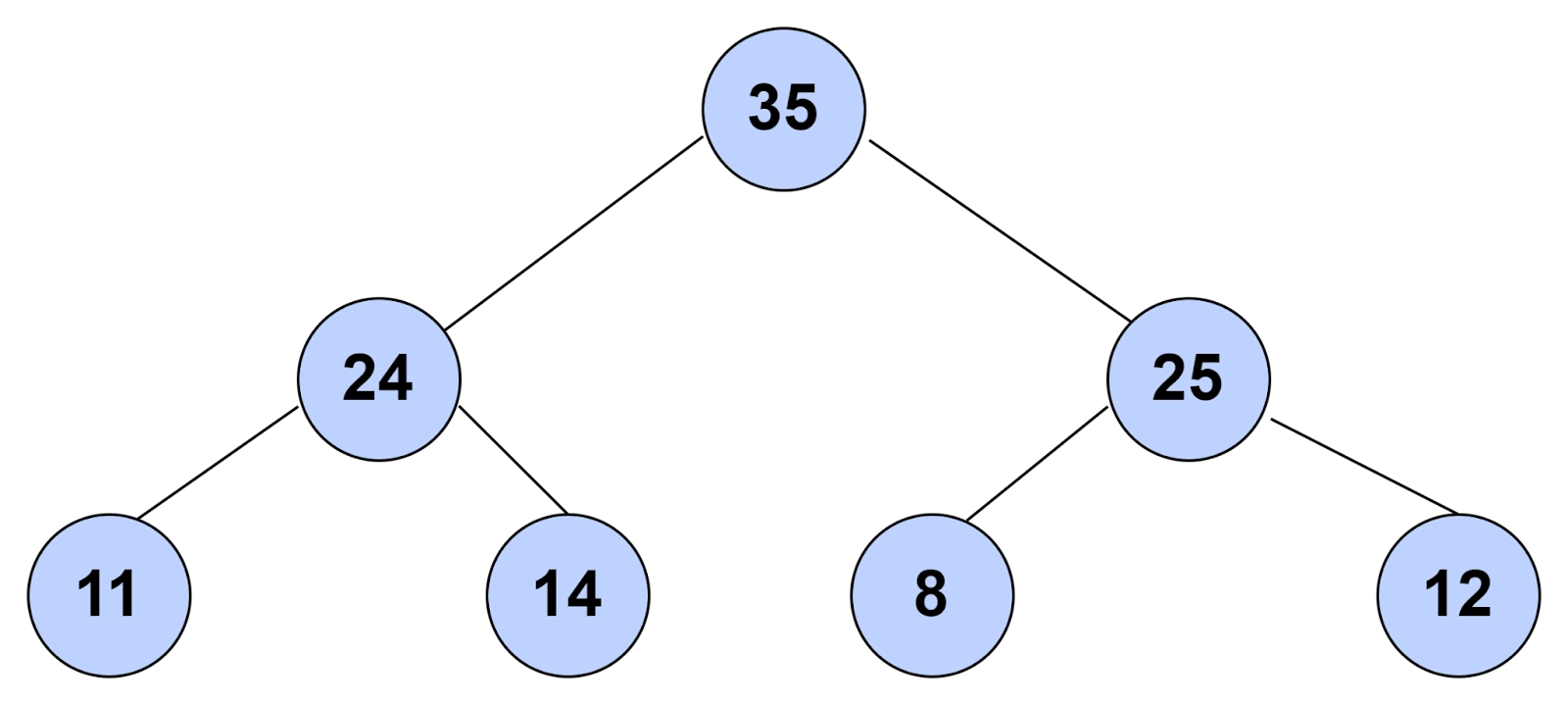
Maximum Heap
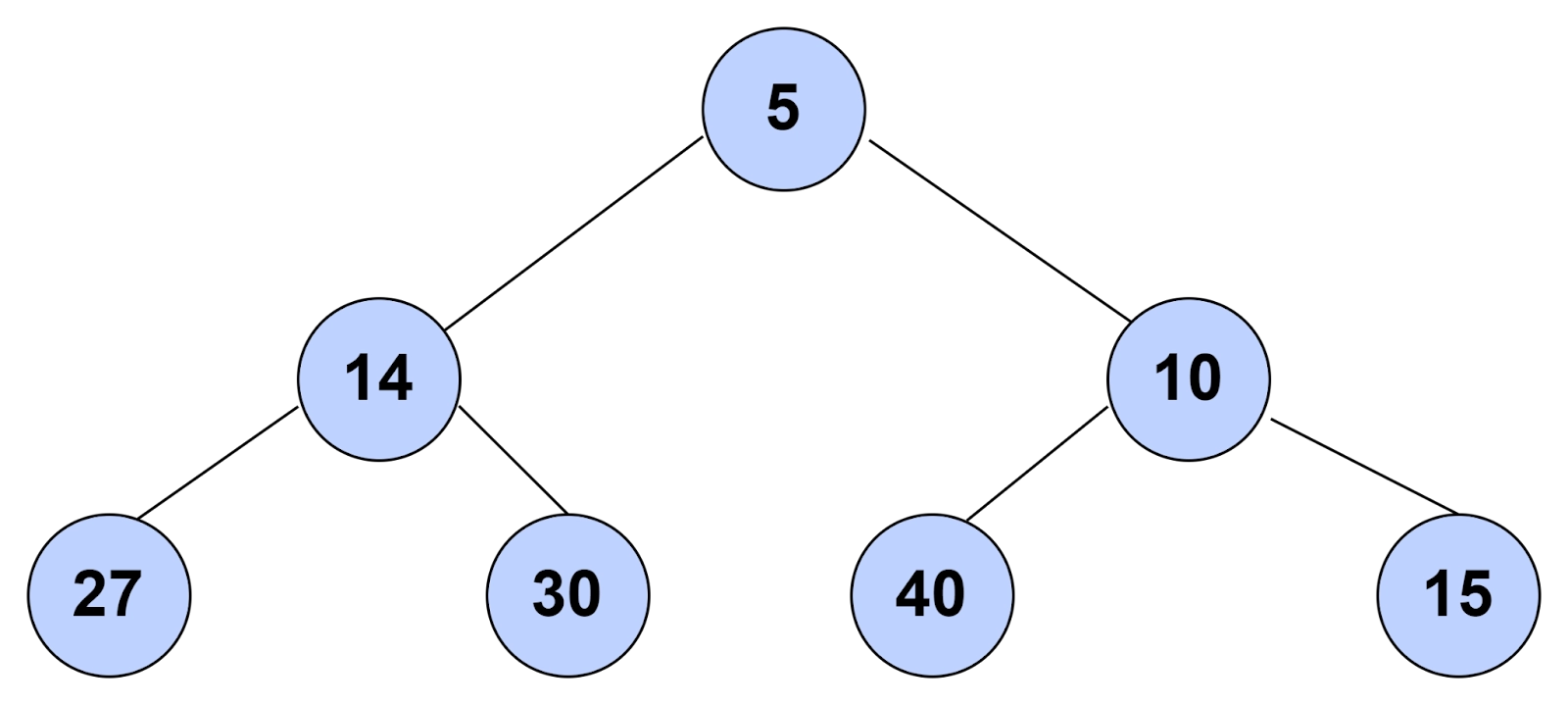
Minimum Heap
15. What is the level order traversal of a tree? Why do we use a queue in a level order traversal of a tree?
Level Order Traversal is a breadth-first traversal of a tree in which we traverse the tree level-wise. In this, we first cover all the nodes of a present level and then move to the next level of the tree.
In level-order traversal, we are supposed to traverse the nodes in the order in which they are stored. That is, while traversing the current level of the tree, we store the nodes of that level first. Now, we will process those child nodes in the order in which they are stored. That's why it is convenient to use a 'queue' data structure as it is a "First In First Out" type of data structure.
16. State the Pseudocode to find the Lowest Common Ancestor in a Binary Tree.
//Function to find Lowest Common Ancestor
int searchLCA(TreeNode node, int n1, int n2)
{
Arrays.fill(first, -1);
entry = 0;
Tour(parent, 0);
obj.segment_tree = constructST(cl, 2 * n2 - 1);
if (first[n1] > first[n2])
n1 = swapping(n1, n1 = n2);
int a = first[n1];
int b = first[n2];
int index = RMQ(obj, 2 * n2 - 1, a, b);
return euler_path[index];
}17. What is a Threaded Binary Tree? Explain its types.
Such a tree in which all right child pointers would be null and pointing towards the inorder successor of the node is known as a threaded binary tree.
Similarly, all left child pointers would also be null and point towards the inorder predecessor of the node.
There are two types of Threaded Binary Trees:
Single Threaded Binary Tree
In this type, if a node has a right null pointer, then this right pointer is threaded towards the in-order successor’s node if it exists. The node structure is similar to that of a Binary Tree. We need some extra boolean variables.
Double-Threaded Binary Tree
In this type, the left null pointer of a node is made to point towards the in-order predecessor node, and the right null pointer is made to point towards the in-order successor node.
18. State an algorithm to perform preorder traversal without using Recursion.
To perform preorder traversal without using Recursion, we need a stack.
- Set the present node as the root
- Check if it is null, then return
- Store the present node value in the container
- Put it right on the stack
- Put left on the stack
- While the stack is not empty
- pop from the stack into the present node. The left will be on top of the stack and taken first.
- Repeat from step 2
19. How can we calculate the diagonal sum of a binary tree?
To calculate the diagonal sum of a binary tree, you need to follow the steps mentioned below.
- Construct an empty map, where each key corresponds to a binary tree diagonal, and each value maintains the total number of nodes that make up the diagonal.
- Update the map after preorder traversal of the tree.
- Increase the diagonal by one for each node's left subtree.
- Repeat with the same diagonal for each node's right subtree.
20. In what way can you find if the two trees are identical?
Two binary trees are considered identical only when they have the same data and arrangement. For that, we will traverse the tree and compare. You can use the algorithm below for your reference.
- Compare data of root node (data1==data2)
- Check left subtree recursively.
Call method ‘Tree( tree1-> left subtree, tree2-> left subtree)’
- Similarly, check the right subtree
- if a,b,c are true, return1
Must Read Recursive Binary Search.
21. What would you do to check if a given binary tree is a subtree of another binary tree?
Suppose that we have a binary tree A. We want to check if a binary tree B is a subtree of binary tree A.
- Check if there is any node in binary tree A, same as in binary tree B.
- Once you get the common node, look out for the neighbor nodes.
- Check if they are the same or not.
- If yes, you can say that binary tree B is a subtree of binary tree A.
22. Why is balancing important when it comes to Binary Trees?
Balancing is important because it results in time optimization. A balanced binary tree optimizes search time in the tree. The worst-case time complexity in a balanced binary tree is O(log n). While in an unbalanced tree, the worst-case time complexity is O(n). So maintaining balance in a tree is beneficial, especially in complex trees.
Balance Factor = height (Left subtree) – height (Right subtree)
23. Write a program to print the bottom view of the Binary Tree.
Approach: We will create a hash map in which each key represents the relative horizontal distance between the current node and the root node and the value contains a pair comprising the node’s value and level number. Then, perform preorder traversal on the tree. You can refer to the conditions from the comments in the implementation below. Print the nodes on the bottom view.
import java.util.Map;
import java.util.TreeMap;
class Treenode
{
int value;
Treenode l = null, r = null;
Treenode(int value) {
this.value = value;
}
}
//Pair Class
class Pair<X, Y>
{
public final X one;
public final Y two;
private Pair(X one, Y two)
{
this.one = one;
this.two = two;
}
public static <X, Y> Pair <X, Y> of(X x, Y y)
{
return new Pair<>(x, y);
}
}
class Main
{
//Recursive function to perform preorder traversal and fill up the map.
public static void print(Treenode parent, int d, int l, Map<Integer, Pair<Integer, Integer>> map)
{
if (parent == null)
return;
//if current level >= maximum level, update the map
if (!map.containsKey(d) || l >= map.get(d).two)
map.put(d, Pair.of(parent.value, l));
//recur the left subtree by decrementing horizontal distance and incrementing level
print(parent.l, d - 1, l + 1, map);
//recur the right subtree by incrementing horizontal distance and decrementing level
print(parent.r, d + 1, l + 1, map);
}
//function to print bottom view
public static void printBottom(Treenode parent)
{
Map<Integer, Pair<Integer, Integer>> map = new TreeMap<>();
print(parent, 0, 0, map);
for (Pair<Integer, Integer> it: map.values())
System.out.print(it.one + " ");
}
public static void main(String[] args)
{
Treenode parent = new Treenode(10);
parent.l = new Treenode(20);
parent.r = new Treenode(30);
parent.l.r = new Treenode(40);
parent.r.l = new Treenode(50);
parent.r.r = new Treenode(60);
parent.r.l.l = new Treenode(70);
parent.r.l.r = new Treenode(80);
printBottom(parent);
}
}
Output:
70 50 80 60
Time Complexity: O(n log n)
Space Complexity: O(n)
24. Write a program to find the size of the largest BST of a binary tree.
Approach: The idea is to traverse the tree in a preorder manner. For each node, check if the child subtree of that node is BST or not. If yes, calculate the size and print the maximum.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
//function to calculate size of BST
public static int number(Treenode parent)
{
if (parent == null)
return 0;
return number(parent.l) + 1 + number(parent.r);
}
//Recursive function to check whether the tree is BST or not.
public static boolean checkBST(Treenode node, int minimum, int maximum)
{
if (node == null)
return true;
if (node.value < minimum || node.value > maximum)
return false;
return checkBST(node.l, minimum, node.value) && checkBST(node.r, node.value, maximum);
}
//function to print the largest BST size
public static int findLargest(Treenode root)
{
if (checkBST(root, Integer.MIN_VALUE, Integer.MAX_VALUE))
return number(root);
return Math.max(findLargest(root.l), findLargest(root.r));
}
public static void main(String[] args)
{
Treenode parent = new Treenode(17);
parent.l = new Treenode(22);
parent.r = new Treenode(15);
parent.l.l = new Treenode(19);
parent.l.r = new Treenode(27);
parent.r.l = new Treenode(12);
parent.r.r = new Treenode(9);
System.out.println(findLargest(parent));
}
}
Output:
3
Time Complexity: O(n^2)
Space Complexity: O(n)
25. Give code to check whether the given binary tree is symmetric or not.
Approach: The idea is to use recursion and check if the right and left subtrees of each level mirror each other or not.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
//Function to check whether child subtrees to parent nodes U and V mirror each other.
public static boolean check(Treenode U, Treenode V)
{
if (U == null && V == null) {
return true;
}
return(U != null && V != null) && check(U.l, V.r) && check(U.r, V.l);
}
//Function to check Symmetric structure
public static boolean check(Treenode root)
{
if (root == null)
return true;
return check(root.l, root.r);
}
public static void main(String[] args)
{
Treenode root = new Treenode(10);
root.l = new Treenode(23);
root.r = new Treenode(36);
root.l.r = new Treenode(45);
root.r.l = new Treenode(60);
if (check(root))
System.out.print("Symmetric");
else
System.out.print("Not symmetric");
}
}
Output:
Symmetric
Time Complexity: O(n)
Space Complexity: O(n)
26. Write a program to check whether the given binary tree is an even-odd tree or not.
Approach: The idea is to check if the children of the nodes at the even level are odd or not. Similarly, check if the children of the nodes at the odd level are even or not. If the condition returns true, the tree is an even-odd tree.
#include <bits/stdc++.h>
using namespace std;
class Treenode
{
public:
int value;
Treenode *l, *r;
Treenode(int value)
{
this->value = value;
this->l = NULL;
this->r = NULL;
}
};
//Recursive function to traverse the tree.
bool isEvenOdd(Treenode * node)
{
if(node==NULL)
return true;
if(node->l!=NULL && abs(node->value - node->l->value)%2==0)
return false;
if(node->r!=NULL && abs(node->value - node->r->value)%2==0)
return false;
return isEvenOdd(node->l) && isEvenOdd(node->r);
}
//Function to check whether the tree is even odd tree or not
bool check(Treenode * parent)
{
if(parent==NULL)
return true;
if(parent->value%2 != 0)
return false;
return isEvenOdd(parent);
}
int main()
{
Treenode *parent = NULL;
parent = new Treenode(0);
parent->l = new Treenode(3);
parent->r = new Treenode(5);
parent->l->l = new Treenode(2);
parent->l->r = new Treenode(4);
parent->r->l = new Treenode(6);
parent->r->r = new Treenode(8);
if (check(parent))
cout << "Yes";
else
cout << "No";
}
Output:
Yes
Time Complexity: O(n)
Space Complexity: O(1)
27. Write the function to print all the ancestors of a given node of the Binary Tree.
Approach: The idea is to traverse the tree in a postorder manner and find the given node. For any node, if the given node is present in its right or left subtree, then the present node is an ancestor of it.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
//Function to print the ancestors
public static boolean print(Treenode parent, Treenode node)
{
if (parent == null)
return false;
if (parent == node)
return true;
boolean l = print(parent.l, node);
boolean r = false;
if (!l)
r = print(parent.r, node);
if (l || r)
System.out.print(parent.value + " ");
return l || r;
}
public static void main(String[] args)
{
Treenode parent = new Treenode(10);
parent.l = new Treenode(20);
parent.r = new Treenode(30);
parent.l.r = new Treenode(40);
parent.r.l = new Treenode(50);
parent.r.r = new Treenode(60);
parent.r.l.l = new Treenode(70);
parent.r.l.r = new Treenode(80);
Treenode node = parent.r.l.l;
print(parent, node);
}
}
Output:
50 30 10
Time Complexity: O(n)
Space Complexity: O(h)
28. State the implementation to print all the cousins of the binary tree.
Approach: The idea is to traverse the tree in preorder manner and find the level of the given node. Then, print all the nodes present in that level.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
//Function to find level of the given node
public static int Level(Treenode parent, Treenode X, int i, int l)
{
if (parent == null || l != 0)
return l;
if (parent == X)
l = i;
l = Level(parent.l, X, i + 1, l);
l = Level(parent.r, X, i + 1, l);
return l;
}
//Function to look for the nodes of that level
public static void print(Treenode parent, Treenode node, int l)
{
if (parent == null)
return;
if (l == 1)
{
System.out.print(parent.value + " ");
return;
}
if (!(parent.l != null && parent.l == node || parent.r != null && parent.r == node))
{
print(parent.l, node, l - 1);
print(parent.r, node, l - 1);
}
}
//Function to print all the required nodes
public static void printCousins(Treenode parent, Treenode node)
{
if (parent == null || parent == node)
return;
int l = Level(parent, node, 1, 0);
print(parent, node, l);
}
public static void main(String[] args)
{
Treenode parent = new Treenode(10);
parent.l = new Treenode(20);
parent.r = new Treenode(30);
parent.l.r = new Treenode(40);
parent.r.l = new Treenode(50);
parent.r.r = new Treenode(60);
parent.r.l.l = new Treenode(70);
printCousins(parent, parent.r.l);
}
}
Output:
40 50
Time Complexity: O(n)
Space Complexity: O(h)
29. Write a program to find the minimum depth of a binary tree.
Approach: The idea is to traverse the tree in a postorder manner. For any node, calculate the depth of its left and right subtrees. Then, print the minimum depth you got.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
//Recursive function to find minimum depth
public static int Depth(Treenode parent)
{
if (parent == null)
return 0;
//To calculate the minimum depth of left subtree
int left = findMinDepth(parent.l);
//To calculate the minimum depth of right subtree
int right = findMinDepth(parent.r);
if (parent.l == null)
return 1 + right;
if (parent.r == null)
return 1 + left;
return Integer.min(left, right) + 1;
}
public static void main(String[] args)
{
Treenode parent = new Treenode(10);
parent.l = new Treenode(20);
parent.r = new Treenode(30);
parent.l.r = new Treenode(40);
parent.r.l = new Treenode(50);
parent.r.r = new Treenode(60);
parent.r.l.l = new Treenode(70);
parent.l.r.r = new Treenode(90);
parent.r.r.l = new Treenode(100);
parent.r.r.l = new Treenode(110);
System.out.println(Depth(parent));
}
}
Output:
3
Time Complexity: O(n)
Space Complexity: O(h)
30. Give the implementation to invert a binary tree.
Approach: The idea is to traverse the tree in a preorder manner. For any node, swap its left and right child. Then, recursively invert the left and right subtrees.
class Treenode
{
int value;
Treenode l, r;
Treenode(int value)
{
this.value = value;
}
}
class Main
{
public static void pre(Treenode parent)
{
if (parent == null)
return;
System.out.print(parent.value + " ");
pre(parent.l);
pre(parent.r);
}
public static void swapping(Treenode parent)
{
if (parent == null)
return;
Treenode t = parent.l;
parent.l = parent.r;
parent.r = t;
}
public static void invert(Treenode parent)
{
if (parent == null)
return;
swapping(parent);
invert(parent.l);
invert(parent.r);
}
public static void main(String[] args)
{
Treenode parent = new Treenode(10);
parent.l = new Treenode(20);
parent.r = new Treenode(30);
parent.l.r = new Treenode(40);
parent.r.l = new Treenode(50);
parent.r.r = new Treenode(60);
parent.r.l.l = new Treenode(70);
invert(parent);
pre(parent);
}
}
Output:
10 30 70 60 20 50 40
Time Complexity: O(n)
Space Complexity: O(h)
Check out this problem - Mirror A Binary Tree




