Table of contents

Introduction

Bitwise Operations in Ruby

2.1.

NOT(~) Operation

2.1.1.

Example

2.1.2.

Output

2.2.

AND(&) Operation

2.2.1.

Example

2.2.2.

Output

2.3.

OR(|) Operation

2.3.1.

Example

2.3.2.

Output

2.4.

XOR(^) Operation

2.4.1.

Example

2.4.2.

Output

Set Operations in Ruby

3.1.

Set Intersection Using AND(&) Operator

3.1.1.

Example

3.1.2.

Output

3.2.

Set Union Using OR(|) Operator

3.2.1.

Example

3.2.2.

Output

Frequently Asked Questions

4.1.

What are the Arithmetic operators in Ruby?

4.2.

Which are bitwise operators in Ruby?

4.3.

What are the different set operations we can perform in Ruby?

Conclusion

Last Updated: Mar 27, 2024

Bitwise NOT(~), AND(&), OR(|) and XOR(^) Operations in Ruby

Author Aniket Majhi

Do you think IIT Guwahati certified course can help you in your career?

Yes

Introduction

Welcome readers! We hope you are doing great.

Ruby is an open-source programming language designed by Yukihiro Matsumoto in the mid-1990s. It was designed with a focus on simplicity and programming productivity. It is a high-level, general-purpose programming language which supports many programming paradigms.

If you want to learn about Ruby, check out our articles on Ruby.

Today, In this article, we will discuss the Bitwise NOT(~), AND(&), OR(|) and XOR(^) Operations in Ruby with proper implementation and explanation. So, follow this article till the end.

So, without further ado, let’s start our discussion.

Bitwise Operations in Ruby

Here in this section, we will discuss different Bitwise operations in Ruby.

NOT(~) Operation

The Not(~) operator is a high precedence unary operator in Ruby. It changes each of the 0 bits in its integer operand to 1 and each of the 1 bits to 0 and produces the binary 1’s complement of the number.

The following result can be shown using the truth table,

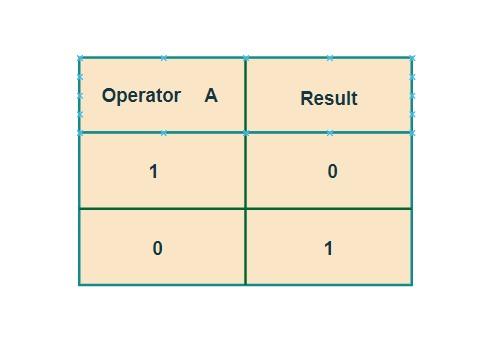
For any integer x, it changes x to ~x, which is nothing but -x-1.

Example

a = 6
puts "Complement(Not) Operator result: "
puts(~a)

You can also try this code with Online Ruby Compiler

Run Code

Output

Complement(Not) Operator result: 
-7

AND(&) Operation

The And(&) operator is a medium precedence binary operator in Ruby. It follows the below truth table,

From the truth table, it is clear that the result of the bits is 1 if and only if both the bits are set to 1.

Example

a = 6
b = 5
puts "Bitwise And(&) operation result: "
puts(a & b)

You can also try this code with Online Ruby Compiler

Run Code

Output

Bitwise And(&) operation result: 
4

OR(|) Operation

The OR(|) operator is also a medium precedence binary operator in Ruby. It follows the below truth table.

From the above truth table, it is clear that we can say that the resultant bit will be 1 if at least one of the bits is set to 1.

Example

a = 6
b = 5
puts "Bitwise OR(|) operation result: "
puts(a | b)

You can also try this code with Online Ruby Compiler

Run Code

Output

Bitwise OR(|) operation result: 
7

XOR(^) Operation

The XOR(^) operator is a medium precedence operator for integers. The truth table of the XOR(Exclusive-OR) is shown below:

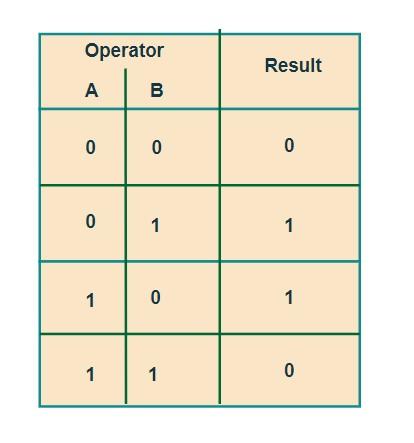
From the above truth table, it is clear that we can say that the resultant bit will be 1 if both the bits are different.

Example

a = 6
b = 5
puts "Bitwise XOR(^) operation result: "
puts(a ^ b)

You can also try this code with Online Ruby Compiler

Run Code

Output

Bitwise XOR(^) operation result: 
3

Set Operations in Ruby

The AND(&) and OR(|) operators can also be used in Arrays for performing different set operations like Set Intersection and Set Union.

Set Intersection Using AND(&) Operator

The set intersection operation takes two arrays as an argument and results in a third object which consists of the elements belonging to both the sets.

Below is an example,

Example

arr1 = [1,2,3,4,5]
arr2 = [3,4,5,6,7]

result = arr1 & arr2

puts "Set Intersection Operation Result: "
puts "#{result}"

You can also try this code with Online Ruby Compiler

Run Code

Output

Set Intersection Operation Result: 
[3, 4, 5]

Set Union Using OR(|) Operator

The set union operation takes two arrays as an argument and results in a third object which consists of the elements belonging to either of the sets.

Below is an example,

Example

arr1 = [1,2,3,4,5]
arr2 = [3,4,5,6,7]

result = arr1 | arr2

puts "Set Union Operation Result: "
puts "#{result}"

You can also try this code with Online Ruby Compiler

Run Code

Output

Set Intersection Operation Result: 
[1, 2, 3, 4, 5, 6, 7]

Read about Bitwise Operators in C here.

Know more about Unary operator overloading in c++ in detail here.

Frequently Asked Questions

What are the Arithmetic operators in Ruby?

The arithmetic operators in Ruby are Addition(+), Subtraction(-),Multiplication(*), Division(/), Exponent(**) and Modulus(%).

Which are bitwise operators in Ruby?

The bitwise operators in Ruby are Bitwise AND(&), NOT(~), OR(|) and XOR(^).

What are the different set operations we can perform in Ruby?

In Ruby, there are mainly three kinds of set operations: Set Union, Set Intersection, Set Difference

Conclusion

In this article, we have extensively discussed Bitwise NOT(~), AND(&), OR(|) and XOR(^) Operations in Ruby.

We hope that through this blog, you have some idea regarding Bitwise NOT(~), AND(&), OR(|) and XOR(^) Operations in Ruby.

If you want to learn more, follow our articles on 8 Reasons Why Ruby Should be Your First Language, Ruby and Ruby On Rails How do they Differ.

Check out this problem - XOR Queries On Tree

Explore our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, interview bundle, follow guided paths for placement preparations and much more.!

Do upvote this blog to help other ninjas grow.

Happy Reading!