Introduction
In the hidden village of leaf, you are a part of team 7. Your sensei Kakashi Hatake and your two comrades had given you a task. You are supposed to convert a BST into a min-heap. But the constraint is you can’t use an array. Now it's up to you, the leader of team 7, to figure out how to do it.

Converting BST into a min-heap without an array is a frequently asked problem in a tech interview. You will also find it in DSA sheets quite popular these days. It is advised to practice such problems during preparation. So let’s start our discussion by converting BST into a min-heap without further ado.
Problem Statement
The "Convert BST into a Min Heap without Using an Array" problem asks you to take BST (binary search tree) as an input. And then convert it into a min-heap. The min-heap should contain all of the binary search tree's elements. We are not supposed to use an array in our approach.

Let’s understand the problem of conversion of BST into a min-heap by some examples.
Sample Examples
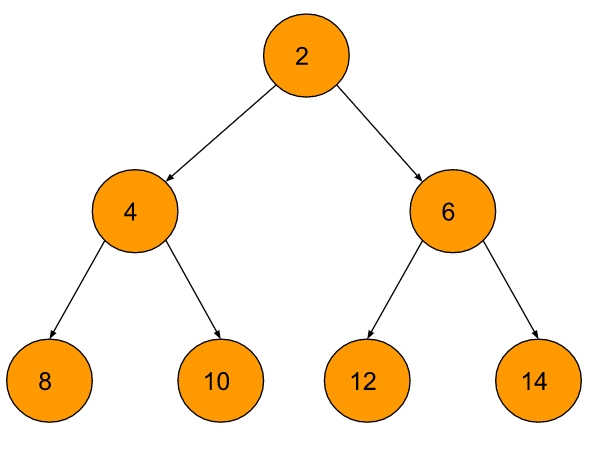
Example 1: Given BST

Output: Min Heap
Linked list and Level Order Traversal Approach
We will use a linked list and level order traversal approach to convert BST into a min-heap. Here, we first convert the tree into a linked list. And then we do a level order traversal.
Now let’s see the algorithm to convert BST into a min-heap.
Algorithm
-
Make a data structure to store a binary tree node.
-
Now make a recursive function to insert a key into the BST. We'll follow three cases in it:
- If the root value is null, create a new node and return it.
- If the given key value is less than the root node, go for the left subtree.
-
And if the given key value is more than the root node, go for the right subtree.
-
Make a helper function to perform level order traversal on a binary tree.
-
Now we have to create a function to construct a complete binary tree from sorted keys in a queue.
-
Construct a queue to store the value of the parent nodes.
-
Initialize the root node of the binary tree, enqueue root node, and loop till all keys are processed.
-
Now create a function to perform in-order traversal on a given binary tree and enqueue all nodes (in encountered order).
- Maintain a queue to store in order traversal on the tree. Fill the queue in an in-order fashion, and construct a complete binary tree from sorted keys in the queue.
Implementation in C++
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <utility>
using namespace std;
// The data structure to store a binary tree node
struct Node
{
int data;
Node* left = nullptr, *right = nullptr;
Node() {}
Node(int data): data(data) {}
};
// Now the recursive function to insert a key into a BST
Node* insert(Node* root, int key)
{
//Now the root is null. create a new node and return
if (root == nullptr) {
return new Node(key);
}
// Now if the given key is less than the root node, recurr for left subtree
if (key < root->data) {
root->left = insert(root->left, key);
}
// Now if the given key is more than the root node, recur for the right subtree
else {
root->right = insert(root->right, key);
}
return root;
}
// The helper function to perform level order traversal on a binary tree
void printLevelOrderTraversal(Node* root)
{
// For base case: empty tree
if (root == nullptr) {
return;
}
queue<Node*> q;
q.push(root);
while (!q.empty())
{
int n = q.size();
while (n--)
{
Node* front = q.front();
q.pop();
cout << front->data << ' ';
if (front->left) {
q.push(front->left);
}
if (front->right) {
q.push(front->right);
}
}
cout << endl;
}
}
// Now, Function to construct a complete binary tree from sorted keys in a queue
Node* construct(queue<int> &keys)
{
// To construct a queue to store the parent nodes
queue<Node*> q;
// Now initialize the root node of the complete binary tree
Node* root = new Node(keys.front());
keys.pop();
// To enqueue root node
q.push(root);
// Now loop till all keys are processed
while (!keys.empty())
{
// To dequeue front node
Node* parent = q.front();
q.pop();
// To allocate the left child of the parent node with the next key
parent->left = new Node(keys.front());
keys.pop();
// to enqueue left child node
q.push(parent->left);
// now if the next key exists
if (!keys.empty())
{
// now allocate the right child of the parent node with the next key
parent->right = new Node(keys.front());
keys.pop();
// to enqueue right child node
q.push(parent->right);
}
}
// now return the root node of the complete binary tree
return root;
}
// the function to perform inorder traversal on a given binary tree and
// enqueue all nodes (in encountered order)
void inorder(Node* root, queue<int> &keys)
{
if (root == nullptr) {
return;
}
inorder(root->left, keys);
keys.push(root->data);
inorder(root->right, keys);
}
// Function to convert a BST into a min heap without using
// any auxiliary space
void convert(Node* &root)
{
// The base case
if (root == nullptr) {
return;
}
// Now maintain a queue to store inorder traversal on the tree
queue<int> keys;
// Now fill the queue in an inorder fashion
inorder(root, keys);
// Now construct a complete binary tree from the sorted keys in the queue
root = construct(keys);
}
int main()
{
vector<int> keys = { 3, 2,5, 4, 8, 10 };
Node* root = nullptr;
for (int key: keys) {
root = insert(root, key);
}
convert(root);
printLevelOrderTraversal(root);
return 0;
}
Output:

Time Complexity
The time complexity of the above approach is O(n). It is because we first converted the tree into a linked list. And then, we did a level order traversal. The two operations used are linear time operations. That is why the time complexity of the approach is O(n).
Space Complexity
The space complexity of the above approach is O(log n). As we used a queue to store the children on a single level. Log space complexity is required. So, the algorithm works in place.
You can also read about insertion into bst.




