Introduction
Hi Ninja! In this article, we will learn to solve the problem of calculating the shortest distance between two nodes in BST. We will use the property of BST that the values of all the nodes in the left subtree are less than the current node's value and the values of nodes in the right subtree are greater than the current node's value.
I hope you will enjoy and have fun learning a medium-level DSA problem on binary search tree♟ "Calculate the shortest distance between two nodes in BST."
Problem Description🗒️
We have been given a binary search tree and two values. We have to find the shortest distance between two nodes having these values. Assume that both values exist in the given BST.
Sample Examples😄
Input 1:
Root of above tree, x = 7, y = 12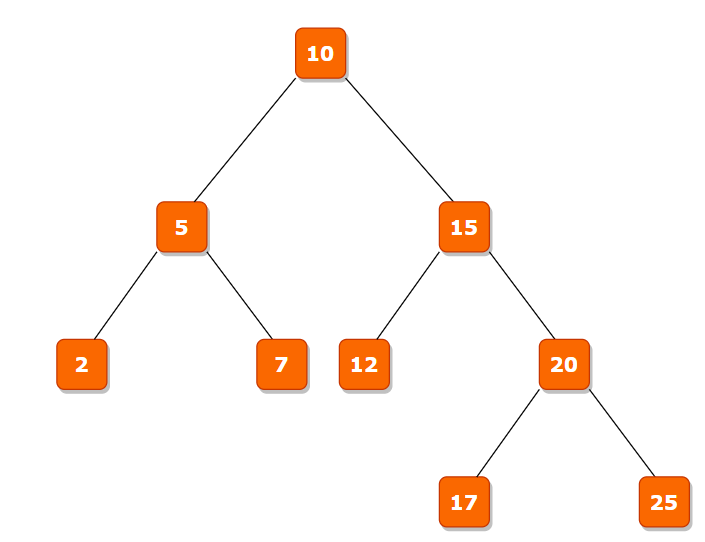
Output:
4
Explanation:
Distance between 7 and 12 in above given BST is 4.
Input 2:
Root of above tree, x = 6, y = 15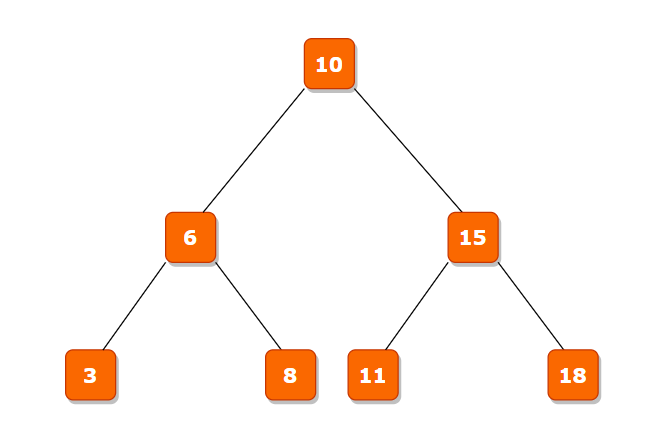
Output:
2
Explanation:
Distance between 6 and 15 in above given BST is 2.
Approach🤖
In the case of Binary Search Trees, we can find the distance between two nodes faster as compared to normal binary trees. In this approach, we will use BST’s properties.
We know that BST follows these properties:
- For a node, all the nodes in the left subtree have values less than the current node's value.
- For a node, all the nodes in the right subtree have values greater than the current node's value.
- The left and right subtree should also be binary search trees and follow all three properties.
Algorithm👽
We will start from the root, and for every node, we do the following:
- If both the given values are smaller than the current node, we move to the left subtree of the current node.
- If both the given values are greater than the current node, we move to the right subtree of the current node.
- If one of the given values is smaller and the other value is greater than the current node, then the current node is the Lowest Common Ancestor (LCA) of the two nodes with the given value.
- We find the distances of the current node from these two given values, and the sum of the distances will be our answer.
C++ Code⌨️
//Program to calculate the
//shortest distance between two nodes in BST
#include <bits/stdc++.h>
using namespace std;
struct Node {
struct Node* left;
struct Node* right;
int value;
};
struct Node* newNode(int value)
{
struct Node* ptr = new Node;
ptr->value = value;
ptr->left = ptr->right = NULL;
return ptr;
}
// Insert function in BST
struct Node* insert(struct Node* root, int value)
{
if (!root)
root = newNode(value);
else if (root->value > value)
root->left = insert(root->left, value);
else if (root->value < value)
root->right = insert(root->right, value);
return root;
}
// This function returns distance of x from root.
int rootDistance(struct Node* root, int x)
{
if (root->value == x)
return 0;
else if (root->value > x)
return 1 + rootDistance(root->left, x);
return 1 + rootDistance(root->right, x);
}
// This returns the minimum distance between x and y.
// assuming that x and y exist in BST.
int distance(struct Node* root, int x, int y)
{
if (!root)
return 0;
// Both values lie on left
if (root->value > x && root->value > y)
return distance(root->left, x, y);
// Both values lie in the right
if (root->value < x && root->value < y)
return distance(root->right, x, y);
// Lie in opposite directions
// Root is the LCA of two nodes
if (root->value >= x && root->value <= y)
return rootDistance(root, x) +
rootDistance(root, y);
}
//function to check x smaller than y
int findDistance(Node *root, int x, int y)
{
if (x > y)
swap(x, y);
return distance(root, x, y);
}
// main
int main()
{
struct Node* root = NULL;
root = insert(root, 10);
insert(root, 5);
insert(root, 15);
insert(root, 2);
insert(root, 7);
insert(root, 12);
insert(root, 20);
insert(root, 17);
insert(root, 25);
int x = 7, y = 12;
cout << findDistance(root, 7, 12);
return 0;
}
Output:
4JAVA Code⌨️
//Program to calculate the
//shortest distance between two nodes in BST
class Ninja {
static class Node {
Node left, right;
int value;
}
static Node newNode(int value)
{
Node ptr = new Node();
ptr.value = value;
ptr.left = null;
ptr.right = null;
return ptr;
}
// Insert function in BST
static Node insert(Node root, int value)
{
if (root == null)
root = newNode(value);
else if (root.value > value)
root.left = insert(root.left, value);
else if (root.value < value)
root.right = insert(root.right, value);
return root;
}
// This function returns the distance of x from the root.
static int distanceFromRoot(Node root, int x)
{
if (root.value == x)
return 0;
else if (root.value > x)
return 1 + distanceFromRoot(root.left, x);
return 1 + distanceFromRoot(root.right, x);
}
// This returns the minimum distance between x and y.
// assuming that x and y exist in BST.
static int distance(Node root, int x, int y)
{
if (root == null)
return 0;
// Both values lie in left
if (root.value > x && root.value > y)
return distance(root.left, x, y);
// Both values lie in right
if (root.value < x && root.value < y) // same path
return distance(root.right, x, y);
// Lie in opposite directions
// Root is the LCA of two nodes
if (root.value >= x && root.value <= y)
return distanceFromRoot(root, x) + distanceFromRoot(root, y);
return 0;
}
//function to check x smaller than y
static int findDistance(Node root, int x, int y)
{
int temp = 0;
if (x > y)
{
temp = x;
x = y;
y = temp;
}
return distance(root, x, y);
}
// Driver code
public static void main(String[] args)
{
Node root = null;
root = insert(root, 10);
insert(root, 5);
insert(root, 15);
insert(root, 2);
insert(root, 7);
insert(root, 12);
insert(root, 20);
insert(root, 17);
insert(root, 25);
int x = 7, y = 12;
System.out.println(findDistance(root, 7, 12));
}
}
Output:
4
Complexity Analysis
Time Complexity: O(H), where H is the height of the given binary search tree. We find the distance of nodes from the LCA and in BST, the maximum number of nodes we have to visit is the tree's height.
Space Complexity: O(H), where H is the height of the BST and O(H) space is required for the call stack.





