Introduction
Calculus is a mathematical concept that studies the continuous change or rate of change in a particular problem. In this blog, we will discuss calculus with the help of the index calculus method. The primary motive of this blog is to make you understand how we can use calculus in cryptography.
Cryptography is a field that studies how to develop efficient algorithms for the encryption of data. Algorithms mainly developed are based on mathematical expressions, so it will be difficult to breach the algorithms using computational power.

The index calculus method is also one of the mathematical concepts that are used to implement cryptography. But before we discuss the relationship between cryptography and index calculus, we need to understand the ElGamal Cryptosystem and discrete logarithm problem.
ElGamal Cryptosystem
The ElGamal Cryptosystem is a public key cryptography system based on the discrete logarithm problem. A discrete logarithm problem is finding an exponent in a particular computational time or time complexity. A discrete Logarithm problem is defined as:
In a multiplicative group (G, ·), an element α ∈ G has order n, and an element β ∈ (α).
Find the unique integer x, 0 ≤ x ≤ n − 1, such that x= β. We will denote integer x by logx= β; it is called the discrete logarithm of β.
A discrete logarithm problem follows the concept of a one-way function. A one-way function is a function that is easier to implement in one way and hard to revert or inverse the implementation. As mentioned, ElGamal Cryptosystem is based on discrete logarithm problems, so let’s understand the one-way function using the ElGamal Cryptosystem.
The ElGamal Cryptosystem is defined as, suppose p is a prime in the Discrete Logarithm problem in (Zp ∗ , ·) is infeasible, and α ∈ Zp ∗ be a primitive root of p. and define K = {(p, α, a, β): = a mod p}.
The values p, α, and β are the public keys, and a is the private key. For K = (p, α, a, β), and for a (secret) random number k ∈ Zp−1, define enc(x, k) = (y1, y2), where y1 = k mod p and y2 = x k mod p.
For y1, y2 ∈ Zp ∗ , define dec(y1, y2) = y2(y1 a ) −1 mod p.
Example
Let's assume Person A wants to send the message X = 911 to person B.
Suppose prime number p = 19 and primitive root α = 3. Now let's consider a = 5.

Now, let's consider k = 3 as the random integer chosen by person A.

And
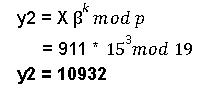
We will send y1 and y2 as ciphertext, and Person B will decipher this using the decryption formula.
According to the definition

By solving the above equation, we get X = 911 which is the message sent from person A to person B.
Points to remember
-
Always remember that a value should be secret and only shared with the receiver on a secured channel to implement the decryption.
-
In ElGamal Cryptosystem, the prime number p and the value will be public.
-
Try to use a huge prime number because a small prime number can be easily computed, and an eavesdropper can guess the secret key very quickly.
- The above problem is an example of a one-way function because, as you can observe, it is not easy to think or compute the value of exponent a for a huge integer.










