Introduction
Binary Trees are one of the most favorite topics when it comes to testing the Data Structures and Algorithms in technical interviews. Not only does it checks on the candidate’s logical skills but also his knowledge of pointers and recursion.
In this article, we will discuss one such problem related to Binary Tree: Check for Children Sum Property in a Binary Tree.
Problem Statement
Given a Binary Tree with nodes having an integer as the data stored in it. Your task is to check if every node of the binary tree follows the children sum property. The children sum property is as follows:
- The value in the node is equal to the sum of the values in its left and right child.
- In case a node has no child, it follows the children sum property by default.
- For NULL nodes, consider the value 0 to be stored in them
Explanation of the problem
In the question, you will be given a binary tree. Your task is to write a function that checks if every node of the tree has a value equal to the sum of its children. If all the nodes of the tree follow the children sum property, it returns true or else false.
Basically, you have to think of something through which you go to every node and see if it stores the sum of its children nodes. If only one child is present, then the parent node should contain that value. Also, as given in the question, if the node has no child or is NULL, then there is no need to check it as it is considered that it already follows the property.
Sample Example
Consider the following binary tree:
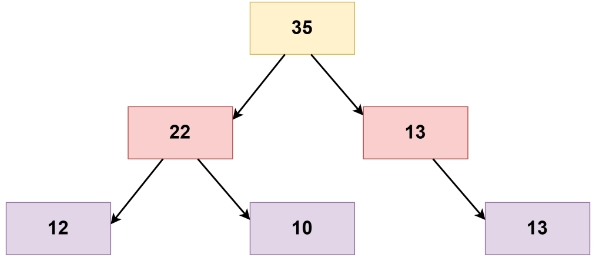
All the nodes of the above binary tree follow the children sum property.
For the root node,
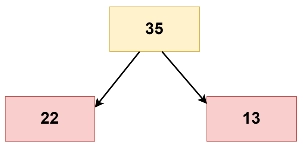
The root node with value 35 has the left child 22 and the right node 13. The condition is satisfied as 35=22+13. Return TRUE.
For its left child,
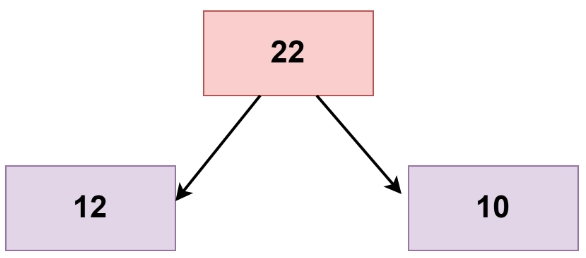
Again as 22=12+8, return TRUE.
For the right child of the root,
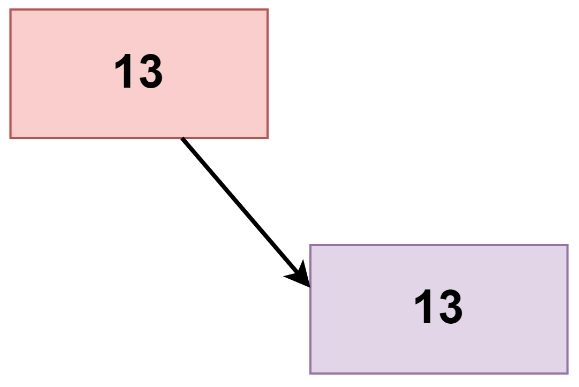
All other nodes are leaf nodes, so automatically, they follow the children sum property.
Now, look at this binary tree:
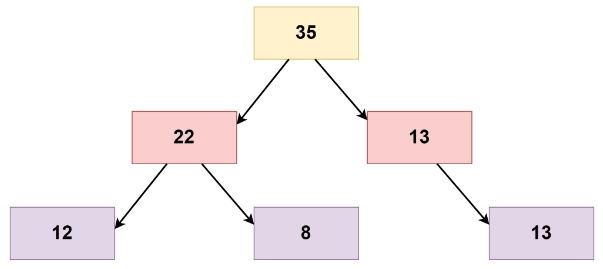
Here, for the root node,

The condition is satisfied.
For the left child of the root node,
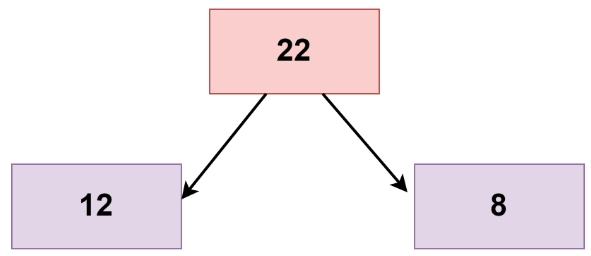
Here, 22!=12+8. So, it returns FALSE from here. Consequently, the whole binary tree does not follow the children sum property.
Approach
Reading the question and its explanation, the first that may hit your mind is traverse all the nodes and simply check if the value it stores is equal to the sum of its children. So, we can go to each node starting from the root node and check the required condition. If it is satisfied, then we return TRUE and move to its child nodes to check the same condition.
If any of the nodes do not follow the condition, return FALSE.
Steps of the approach
-
Check if one of the following conditions is satisfied and return TRUE or FALSE accordingly :
→ It is a leaf node
→ If both the left child and right child are present, then the sum of the left child and right child is equal to the value of the node.
→ If only the left or right child is present, then its value is equal to the value of the node. - Repeat step 1 for the left child and right child of the node
- Repeat steps 1 and 2 for all the nodes.
Implementation in C++
#include<bits/stdc++.h>
using namespace std;
class node //node of the binary tree
{
public:
int val;
node* left,* right;
};
node* new_node(int value) //Creating a new node
{
node* t=new node;
t->val=value;
t->left=t->right=NULL;
return t;
}
bool children_sum_property(node* current) //function to check the childrren sum property
{
int add=0;
if(current== NULL||(current->left==NULL&¤t->right==NULL))
return true;
else
{
if(current->left!=NULL)
add+=current->left->val;
if(current->right!=NULL)
add+=current->right->val;
return ((current->val==add)&&children_sum_property(current->left)&&children_sum_property(current->right));
}
}
int main()
{
node *root=new_node(35);
root->left=new_node(22);
root->right=new_node(13);
root->left->left=new_node(12);
root->left->right=new_node(10);
root->right->right=new_node(13);
if(children_sum_property(root))
cout<<"This binary tree satisfies the Children Sum Property";
else
cout<<"This binary tree does not satisfy the Children Sum Property";
return 0;
}
Output:
This binary tree satisfies the Children Sum Property Complexity Analysis
Time Complexity: O(n)
Here, n is the total nodes in the tree. All the nodes of the tree are traversed, making the time complexity linear.
Space Complexity: O(n)
Here, n is the total nodes in the tree. The worst-case occurs in the case of the skewed binary tree.




