Introduction
In this blog, we will look at the approach to check whether the given binary tree is a subtree of another binary tree or not.
Problem Statement
Given: A binary tree S, such that it might be a possible subtree of another binary tree T.
Problem: Check whether the given binary tree is a subtree of another binary tree or not. If the binary tree is a subtree, the function will return a true value and if the binary tree is not a subtree, then the function will return a false value.
Sample Examples
Let us consider the following example trees.
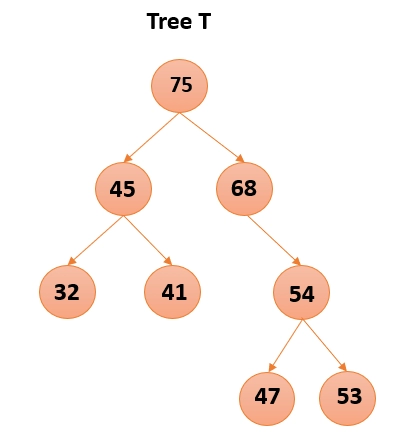
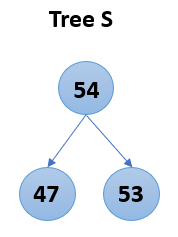
In this example, we can see that the given tree S is a subtree of the tree T. Hence, if we check whether the given binary tree is a subtree of another binary tree or not, the function will return a true value.
Brute Force Approach
In the brute force approach, we can traverse the given trees and mark every node as visited or not and simultaneously compare if the two nodes from each tree are identical or not. If they are identical, we can match the children nodes of that particular node and completely check whether the given binary tree is a subtree of another binary tree or not.
Pseudocode
The pseudocode is as follows:
- Start with traversal of the given binary trees.
- Iterate over every node from the root node in any order - preferably preorder of both the trees.
- Compare the nodes from both trees, if similar then check for the similarity of children nodes.
- If children nodes are also similar, return true value indicating that the given binary tree is a subtree of another binary tree.
- If not, return false value.
Implementation in C++
/* Program to check whether the given binary tree is a subtree of another binary tree or not */
#include<bits/stdc++.h>
using namespace std;
/* Declare a class for the tree tnode*/
class tnode
{
public:
int info;
tnode* lchild;
tnode* rchild;
};
/* function to check whether trees are identical or not */
bool Identical(tnode * r1, tnode *r2)
{
if (r1 == NULL && r2 == NULL)
return true;
if (r1 == NULL || r2 == NULL)
return false;
/* Check if the info of both root tnode and left and right subtree is same or not */
return (r1->info == r2->info &&
Identical(r1->lchild, r2->lchild) &&
Identical(r1->rchild, r2->rchild) );
}
/* This function returns true value if S is a subtree of T, else false */
bool isSubtree(tnode *T, tnode *S)
{
if (S == NULL)
return true;
if (T == NULL)
return false;
if (Identical(T, S))
return true;
/* Check for left and right subtrees */
return isSubtree(T->lchild, S) || isSubtree(T->rchild, S);
}
/* Function to allocate a new tnode with the given info and NULL left and right pointers. */
tnode* newTnode(int info)
{
tnode* Tnode = new tnode();
Tnode->info = info;
Tnode->lchild = NULL;
Tnode->rchild = NULL;
return(Tnode);
}
/* Driver code*/
int main()
{
// TREE T
tnode *T = newTnode(35);
T->rchild = newTnode(9);
T->rchild->rchild = newTnode(9);
T->lchild = newTnode(15);
T->lchild->lchild = newTnode(24);
T->lchild->lchild->rchild = newTnode(36);
T->lchild->rchild = newTnode(7);
// TREE S
tnode *S = newTnode(15);
S->rchild = newTnode(7);
S->lchild = newTnode(24);
S->lchild->rchild = newTnode(36);
if (isSubtree(T, S))
cout << "Tree S is subtree of Tree T";
else
cout << "Tree S is not a subtree of Tree T";
return 0;
}
Implementation in Python
# Program to check whether the given binary tree is a subtree of another binary tree or not
class Tnode:
# Constructor for creating a new node
def __init__(self, info):
self.info = info
self.lchild = None
self.rchild = None
# Function to check if trees are identical or not
def Identical(r1, r2):
if r1 is None and r2 is None:
return True
if r1 is None or r2 is None:
return False
# Check if the info of both roots and left and right subtrees are also same
return (r1.info == r2.info and
Identical(r1.lchild , r2.lchild) and
Identical(r1.rchild, r2.rchild)
)
# This function returns True if S is a subtree of T, else False
def isSubtree(T, S):
if S is None:
return True
if T is None:
return False
if (Identical(T, S)):
return True
# Check left and right subtrees
return isSubtree(T.lchild, S) or isSubtree(T.rchild, S)
# Main Program
#TREE T
T = Tnode(35)
T.rchild = Tnode(9)
T.rchild.rchild = Tnode(9)
T.lchild = Tnode(15)
T.lchild.lchild = Tnode(24)
T.lchild.lchild.rchild = Tnode(36)
T.lchild.rchild = Tnode(7)
# TREE S
S = Tnode(15)
S.rchild = Tnode(7)
S.lchild = Tnode(24)
S.lchild.rchild = Tnode(36)
if isSubtree(T, S):
print ("Tree S is subtree of Tree T")
else :
print ("Tree S is not a subtree of Tree T")
Output:
Tree S is subtree of Tree TComplexity Analysis
Time Complexity: In this approach, as we have traversed over each node from both the binary trees, where there are m nodes in tree T and n nodes in tree S, therefore, we have traversed over (mxn) nodes in total and hence, the time complexity is O(mxn). If the number of nodes are the same in both the trees, i.e., n nodes then the time complexity will be O(n2).
Space Complexity: We have utilised the auxiliary space of O(n) in this program.





