Check If a String is a Palindrome or Not

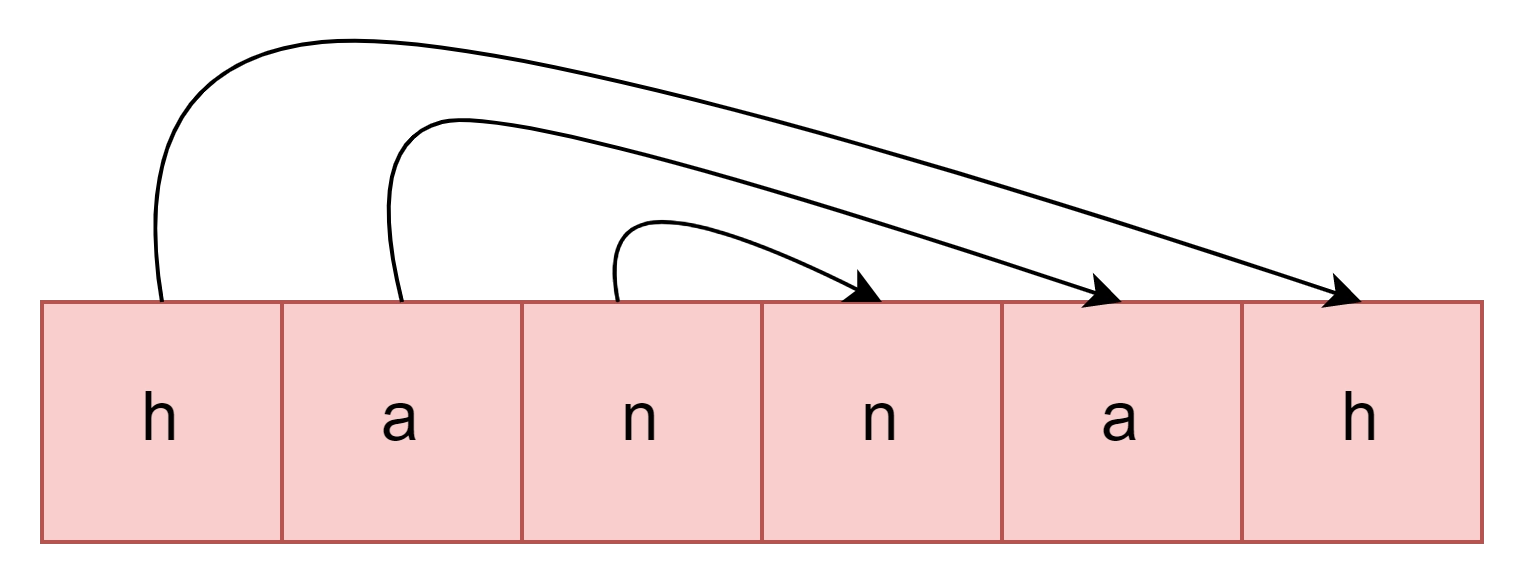
Properties of a Palindrome:

The key properties of a palindrome include:

• Symmetry: Palindromes exhibit symmetry, meaning the sequence looks the same whether read from left to right or right to left.
   
• Character Equality: Each character in the sequence has a corresponding character at the same position when read in reverse, maintaining equality.
   
• No Effect on Reversal: Reversing the order of characters in a palindrome does not alter the sequence; it remains unchanged.

How to identify a Palindrome?

To identify a palindrome, you can follow these steps:

1. Remove Spaces and Punctuation: Eliminate spaces and punctuation from the sequence to focus only on alphanumeric characters.
    
2. Convert to Lowercase: Convert all characters to lowercase (or uppercase) to ensure case consistency.
    
3. Compare Original and Reversed Versions: Create a reversed version of the sequence and compare the original sequence with its reversed counterpart.
    
4. Check for Equality: If the original and reversed sequences are the same, the given sequence is a palindrome. If there is any difference, the sequence is not a palindrome.

Problem Statement

The problem statement that this article deal with is “Check whether a given string is Palindrome or not.” A palindrome is a string that remains the same even after it is reversed. Let's look at some approaches of solving this problem.

Brute Force Approach

1. The brute force approach to this problem is to use the inbuilt STL reverse function. 
2. We will copy the string S into another string A, and then we will reverse the string A.
3. After that, we will compare if strings S and A are equal or not. If they are equal, then S is a palindrome. Otherwise, S is not a palindrome.

Pseudocode

string checkPalindrome(string S)
{
    string A = S;
    reverse(A.begin(), A.end());
    if (S == A) {
        return "Yes";
    }
    else {
        return "No";
    }
}

Implementation in C++

// C++ program to check if a string is palindrome
#include <bits/stdc++.h>
using namespace std;

string checkPalindrome(string S)
{
    // to store the revered string
    string A = S;

    // reverse the string A
    reverse(A.begin(), A.end());

    // If S is equal to A
    if (S == A) {
        return "Yes";
    }
    // Else
    else {
        return "No";
    }
}

// Driver Code
int main()
{
    string S = "ABBA";
    cout << checkPalindrome(S);

    return 0;
}

Output

Input:  "ABBA"
Output: YES

Complexity Analysis

Time Complexity:  O(N), as reverse() takes O(N) time complexity to reverse the string.

Space Complexity: O(N), Since we are using another string to store the reversed string, therefore, the space complexity will be equal to O(N).

Recursive Approach

1. In the recursive approach, we will traverse the string from [0, N/2], where N is the length of the string.
2. While traversing, we will check if S[i] == S[N-i-1], and if it is equal, then we will continue with recursion calls. Else, we will return false. 
3. If the output of the recursive function is true, then we will print "YES"; else, we will print "NO."

PsuedoCode

bool checkPalindrome(string S, int i)
{
    if (i > S.size() / 2)
    {
        return true;
    }
    return S[i] == S[S.size() - i - 1] && checkPalindrome(S, i + 1);
}

Implementation in C++

// C++ code to check if a string is a palindrome
#include <bits/stdc++.h>
using namespace std;

bool checkPalindrome(string S, int i)
{

    if (i > S.size() / 2)
    {
        return true;
    }

    return S[i] == S[S.size() - i - 1] && checkPalindrome(S, i + 1);
}

int main()
{
    string str = "nun";
    if (checkPalindrome(str, 0))
    {
        cout << "YES";
    }
    else
    {
        cout << "NO";
    }
}

Output

Input:  "NUN"
Output: YES

Complexity Analysis 

Time Complexity:  O(N), as we check for the equality of characters from start and end until we reach the mid of the string.

Space Complexity: O(N), due to the space consumed by the recursive call stack as we check for the equality of characters from start and end.

Optimal Approach

1. The above approach can be optimized if we remove the extra space we are using to check if a string is a palindrome.
2. We will traverse the string from [0, N/2] where N is the length of the string, and at every iteration, we will check if S[i] == S[N-i-1] and if it is equal, then we will continue else we will break from the loop and return "NO." 
3. If the iteration is complete, then we will return "YES."

PsuedoCode

string checkPalindrome(string S)
{
    int N = S.length();
  
    for (int i = 0; i < N/2; i++) {
        if (S[i] != S[N - i - 1]) {
            return "NO";
        }
    }
    return "YES";
}

Implementation in C++

// C++ code to check if a string is a palindrome
#include <bits/stdc++.h>
using namespace std;

string checkPalindrome(string S)
{
    int N = S.length();
    // to iterate over the range [0, N/2]
    for (int i = 0; i < N/2; i++) {

        // if the condition is not satisfied then return "NO"
        if (S[i] != S[N - i - 1]) {
            return "NO";
        }
    }
    return "YES";
}

// Driver Code
int main()
{
    string S = "NOON";
    cout << checkPalindrome(S);

    return 0;
}

Output

Input:  "NOON"
Output: YES

Complexity Analysis

Time Complexity:  O(N), as we need to check for equality of characters from start and end until the mid of the length of the string.

Space Complexity: O(1), Since we are not using any extra string or a recursive call stack, therefore, the space complexity will be equal to O(N).

Also read palindrome number in python.

Frequently Asked Questions

What is an example of a palindrome string?

An example of a palindrome string is "racecar." It reads the same forwards and backwards, maintaining its original sequence when reversed. Palindromes are used in various applications, including wordplay and data validation.

How do you check if a string is palindrome or not?

To check if a string is a palindrome, remove non-alphanumeric characters, convert to lowercase, and compare the original with its reversed version.

What is a palindromic substring?

A palindromic substring is a sequence of characters within a string that reads the same forward and backward.

Conclusion

This article discussed the problem to check if a string is a palindrome or not. We have discussed three approaches to solve this problem. The first one is the brute force, the second is the recursive approach, and the last one is the optimal approach.
We have also discussed the time and space complexities of every approach.

Suggested Links -

• String Palindrome
   
• Check Palindrome
   
• Reverse A String In C
   
• Introduction to Recursion