Introduction
In this blog, we will discuss how to Check if all leaves are at the same level. Such problems are fairly common interview questions as well asked in many contests. Before solving the problem, it’s recommended to have a good understanding of binary trees. In this Blog we will dive deep into each detail to get a firm hold over how we can reach from a brute force solution to an optimal solution .
Problem Statement
Given a root to a binary tree. Check if all leaves are at the same level. Return true if all leaves are at the same level. Otherwise return False.
Sample Example
Input:
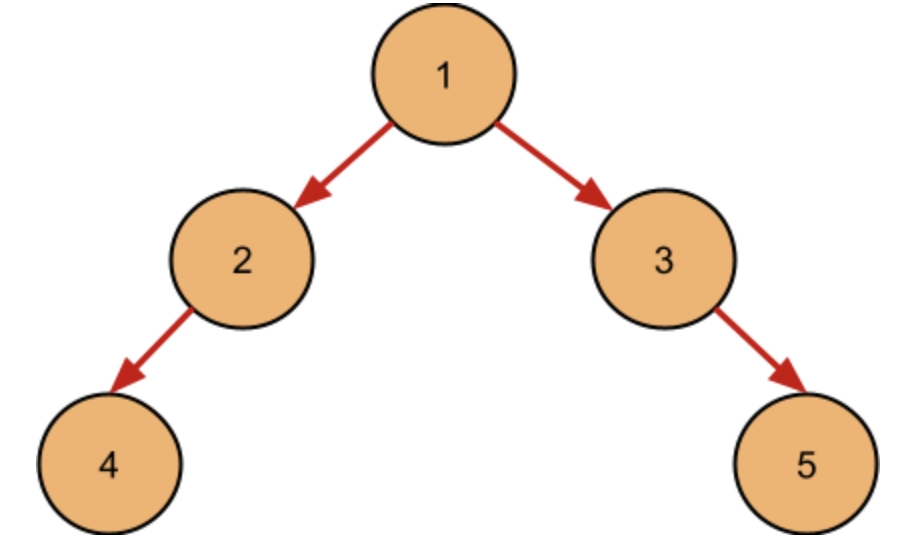
Output: True
Explanation: All the leaves in the binary tree given above are at the same level - 2(taking root to be at level 0).
Brute Force Approach
First, let’s look at the naive approach that would probably strike anybody’s mind before jumping to an optimal approach. We need to Check if all leaves are at the same level.
So, the basic approach is to store the level of each leaf node and compare if all levels are equal or not.
So the naive/basic approach could be formulated as:
- Find the level of each binary tree leaf node and store them in a map.
- Check if all the levels stored in the map are equal or not.
- Return True in case levels are the same .
- Otherwise return False.
NOTE: we could store the levels either iteratively via a simple BFS or using a DFS Algorithm traversal on the binary tree also.
Now let’s look at the PseudoCode.
PseudoCode
Algorithm
___________________________________________________________________
procedure computeLeafNodeLevels(rootNode, level, leafNodeLevels):
___________________________________________________________________
1. if rootNode is NIL do
2. return
3. else if isLeafNode(rootNode) is True do
4. leafNodeLevels[rootNode] ← level
5. return
6. else do
7. computeLeafNodeLevels(rootNode.left, level+1, leafNodeLevels)
8. computeLeafNodeLevels(rootNode.left, level+1, leafNodeLevels)
9. end if
10. end procedure
___________________________________________________________________
procedure checkAllLeavesAtSameLevel(rootNode):
___________________________________________________________________
1. leafNodeLevels ← map to store the level of all leaf nodes.
2. computeLeafNodeLevels(rootNode, 0, leafNodelevels)
3. initialLeafLevel ← initialised to any value from leafNodelevel map
4. for each node, level in leafNodeLevels do
5. if initialLeafLevel != level do
6. return False
7. end if
8. end if
9. return True
10. end procedure
___________________________________________________________________
Implementation in C++
// program to check if all leaves are at the same level
#include <bits/stdc++.h>
#define Node struct BinaryTreeNode
using namespace std;
// binary tree node
struct BinaryTreeNode{
int val;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int nodeValue){
val = nodeValue;
left = nullptr;
right = nullptr;
}
};
// check if a node is a leaf node or not
bool isLeafNode(Node* node){
return !node->left and !node->right;
}
// compute all leaf node levels
void computeLeafNodeLevels(Node* rootNode, int level, map<Node*, int> &leafNodeLevels){
// if rootNode is null return
if(rootNode==nullptr){
return;
}
// if it's a leaf node store its level
else if(isLeafNode(rootNode)){
leafNodeLevels[rootNode] = level;
return;
}
//compute leaf node levels on both left and right subtrees
else{
computeLeafNodeLevels(rootNode->left, level+1, leafNodeLevels);
computeLeafNodeLevels(rootNode->right, level+1, leafNodeLevels);
}
}
// function to check All Leaves are at the SameLevel
bool checkAllLeavesAtSameLevel(Node* rootNode){
map<Node*, int> leafNodeLevels; // map containing levels of all leaf Nodes
computeLeafNodeLevels(rootNode, 0, leafNodeLevels); // compute all leaf node levels
int initialLeafLevel = (*leafNodeLevels.begin()).second; //store the initialLeafLevel
for(auto it = leafNodeLevels.begin(); it!=leafNodeLevels.end(); ++it){
int level = (*it).second; // level of the leaf node
if(initialLeafLevel != level){
return false; // return false if not same
}
}
return true; // return true since all levels are same
}
int main() {
// create the sample binary tree here
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->right = new Node(5);
// find whether all the leaves are at the same level or Not
cout<<(checkAllLeavesAtSameLevel(root)?"True":"False")<<'\n';
return 0;
}
Output:
True
Complexity Analysis
Time Complexity: O(nlogn)
This is because we iterate through the entire binary tree once to store the levels of all leaf nodes. But since the map is being used and takes O(logn) time in the worst case. Hence the time complexity.
Space complexity: O(n) at the worst case because we are storing the levels of all leaf nodes and the recursion stack being used.
The above algorithm works in O(nlogn) time. Can we improve our solution in terms of both space and time??
So let’s think about an efficient approach to solve the problem.




