Sample Examples
Example 1
Input: arr[] { 5, 10, 17, 18, 20, 27, 28}
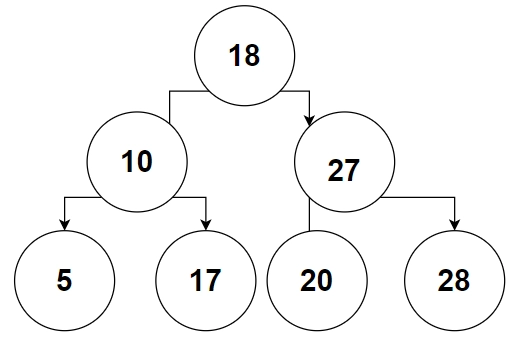
Output: Yes, It’s in inorder
Explanation: Because the given array is sorted, It is inorder. Just like shown in image below, we simply need to check whether the given element is greater than the previous element or not. That’s exactly what we are doing as shown in the image below.
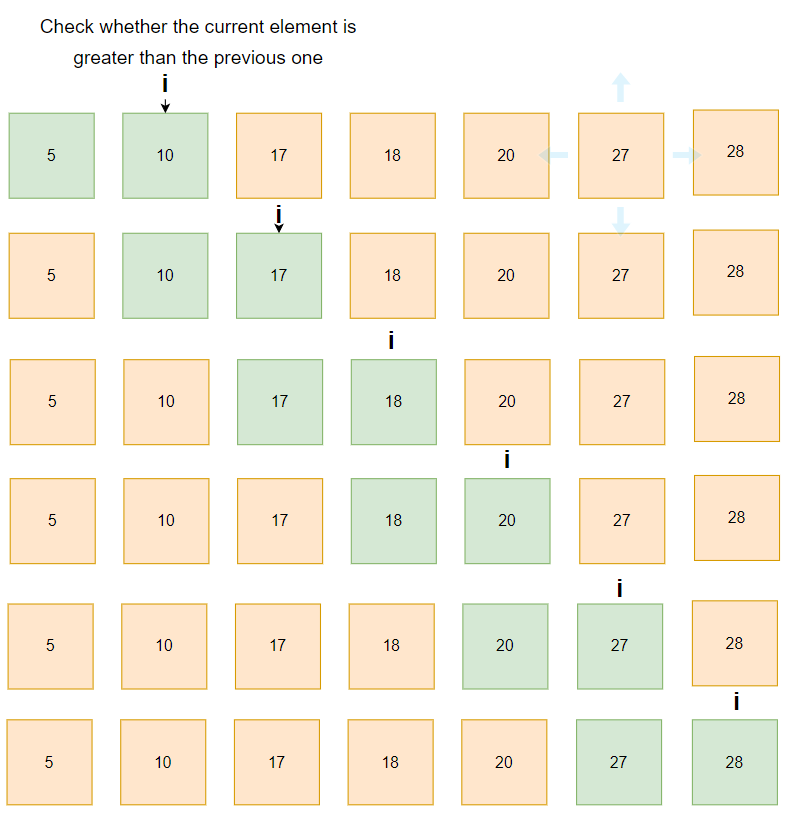
Intuition
From the example and diagram above, you can observe that an array will always represent the inorder of BST if it is ordered. Hence, to Check if an array represents the Inorder of BST or not, we simply need to check whether the given array is sorted or not.
You can check if the array is unsorted, then the given tree will not be a binary search tree.
Approach
To Check if an array represents the Inorder of BST, we will iterate through the array, and we will check whether the current element is greater than the previous element.
Algorithm
n= arr.size()
for i in range 1 to n-1, do
If arr[i-1] > arr[i], then
Return false;
Return true;
Implementation in C++
// A C++ code to determine whether or not an array is sorted.
// Solution of the problem “Check if an array represents the Inorder of BST”
#include<bits/stdc++.h>
using namespace std;
/*
The function that determines whether or not an array is traversed in
order by any binary search tree returns true.
*/
bool checkInorder(vector<int>& arr) {
// check whether the array has an element or not
if (n == 0 || n == 1)
return true;
int n = arr.size();
for (int i = 1; i < n-1; i++)
// Found an unsorted pair
if (arr[i-1] > arr[i])
return false;
// Found no unsorted pairs
return true;
}
// Driver code
int main() {
vector<int> arr { 5, 10, 17, 18, 20, 27, 28} ;
if (checkInorder(arr))
cout << "Yes, It’s in inorder";
else
cout << "No, It’s not in inorder";
return 0;
}
Time Complexity ⌛

The time complexity of the problem “Check if an array represents the Inorder of BST” using the above approach is O(N), where N is the number of elements in the array.
Space Complexity 🚀

The space complexity of the problem “Check if an array represents the Inorder of BST” using the above approach is O(1) as we are not using any auxiliary space.
Check out this problem - Search In Rotated Sorted Array
Frequently Asked Questions ⁉️
What is a binary tree?
A binary tree is a tree data structure having a maximum of two children. There can only be two children per element in a binary tree; hence we usually refer to them as the left and right children.
What is a binary search tree?
A binary search tree is a binary tree in which all of the nodes left to the root node have values less than the root node, and all of the nodes right to the root node have values greater than the root node.
What is a Full Binary Tree?
A full binary tree is a particular kind of binary tree in which every parent node and internal node either has two children or none at all.
What benefits does binary search offer?
Because the amount of data to be searched is reduced by half with each step in a binary search, one of its key benefits is that it is faster than a serial search.
How can I discover the BST inorder traversal?
You move from the left subtree to the root, then to the right subtree when using Inorder.
Conclusion
In this article, we have discussed a coding problem in which we have to Check if an array represents the Inorder of BST. We have seen the question's solution, time, and space complexity(Check if an array represents the Inorder of BST).
If you think this blog has helped you enhance your knowledge about the above question, and if you want to learn more, check out our articles.
And many more on our website.
Visit our website to read more such blogs. Make sure that you enroll in the courses we provide, take mock tests, solve problems available, and interview puzzles. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations. Do upvote our blog to help fellow ninjas grow.