Introduction
Nowadays, problems based on Binary Tree are a Hot topic for many companies and are frequently asked in Goldman Sachs, Microsoft, and Amazon. So, do you want to become a ninja and get into these giant companies?
Today this article will discuss one of those problems based on Binary Tree.
Problem Statement
We were given a Binary Tree with N nodes. Check if removing an edge can divide the Binary Tree into two halves.
Sample Example
Input:
We are given a given a Binary Tree of size n. A particular node can have maximum of two children.You
are given root node of the binary tree.
Output:
This Binary Tree can be splitted Into Two Parts Of Equal Size.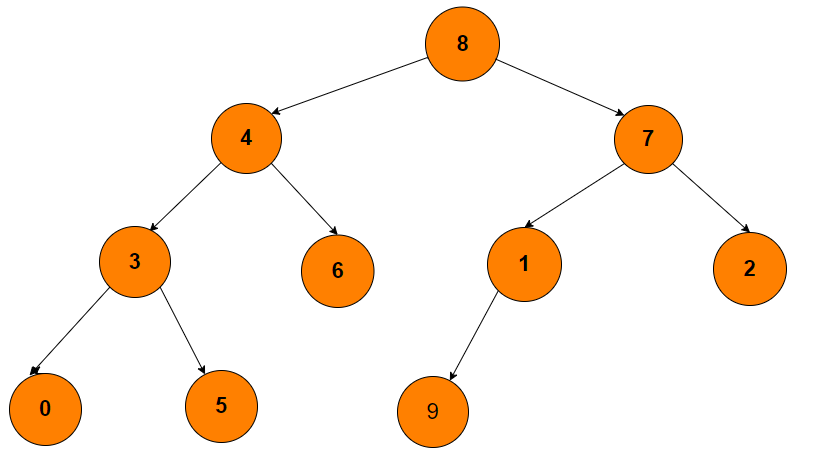
In the given figure, If we cut the left root edge, the Tree is divided into two parts of equal size. The left part of the Tree has a size of 5, and the right part of the Tree also has five nodes.
Brute Force Approach
The Approach is very simple. It is a Recursive. First, we calculate the total number of nodes in the Binary Tree. If the Total number of nodes in the Binary Tree is odd, then return false. Now, We will traverse the entire Tree, and For every Node, find the number of nodes in the subtree. If the number of nodes in the subtree is half the total Node, then return true.
Implementation in C++
#include <iostream>
using namespace std;
// Structure and Creation Of New Node
struct Node
{
int data;
Node *left;
Node *right;
Node(int val)
{
data = val;
left = right = NULL;
}
};
// Function To find total Number of Node in Binary Tree
int TotalNumberOfNode(Node *root)
{
if (root == NULL)
return 0;
int NodesInLeftSubtree = TotalNumberOfNode(root->left);
int NodesInRightSubtree = TotalNumberOfNode(root->right);
int total = NodesInLeftSubtree + NodesInRightSubtree + 1;
return total;
}
bool IsSplitingingTree(Node *root, int n)
{
// Base cases
if (root == NULL)
return false;
// Calculating number of nodes for every subtree in given tree
int x = TotalNumberOfNode(root);
// If number of nodes in a particular subtree is half of total number of tree
if (x == n / 2)
return true;
// Checking If Left Subtree has any dividing Edge
bool LeftSubtree = IsSplitingingTree(root->left, n);
// Checking If Left Subtree has any dividing Edge
bool RightSubtree = IsSplitingingTree(root->right, n);
// Taking Union (means whole tree has traversed)
bool ans = LeftSubtree || RightSubtree;
return ans;
}
int main()
{
// Creation Of Tree
struct Node *root = new Node(8);
root->left = new Node(4);
root->right = new Node(7);
root->left->left = new Node(3);
root->left->right = new Node(6);
root->right->left = new Node(1);
root->right->right = new Node(2);
root->left->left->left = new Node(0);
root->left->left->right = new Node(5);
root->right->left->left = new Node(9);
// Counting Total Number Of nodes in given tree
int n = TotalNumberOfNode(root);
if (n % 2 != 0)
{
cout << "This Binary Tree cannot be splitted Into Two Parts Of Equal Size" << endl;
return 0;
}
// Recursive function to check whether the tree is dividing between anywhere.
bool splitfunction = IsSplitingingTree(root, n);
if (splitfunction == 1)
{
cout << "This Binary Tree can be splitted Into Two Parts Of Equal Size" << endl;
}
else
{
cout << "This Binary Tree cannot be splitted Into Two Parts Of Equal Size" << endl;
}
return 0;
}
Output:
This Binary Tree can be splitted Into Two Parts Of Equal Size
Complexity Analysis
Time complexity: O(n²), where n is the number of nodes in a tree.
As there are n nodes in a binary tree and we are using a loop for every node,Hence, our time complexity is O(n²).
Space complexity: O(n).
We are using Recursion and it makes a stack of size n.Hence Space complexity is O(n).




