Check If Two Given Sets Are Disjoint

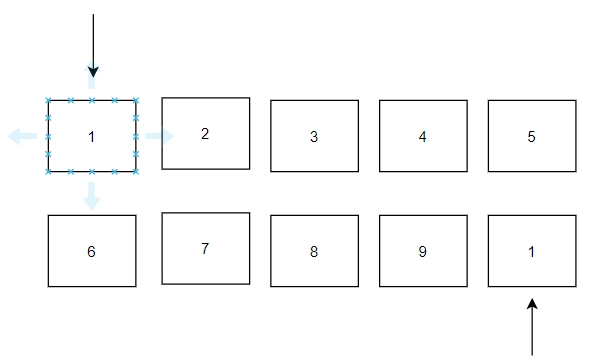
Example

Input: 

SetA[] = {1, 2, 3, 4, 5} & SetB[] = {6, 7, 8, 9, 1}

Output: 

Not Disjoint

Reason: 1 is common in two sets.

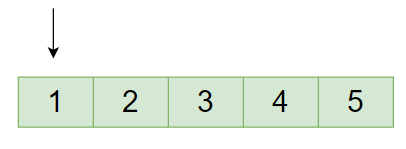
Input: 

SetA[] = { 1, 2, 3, 4 } & SetB[] = {5, 6, 7, 8}

Output: 

Disjoint 

Reason: The two sets have nothing in common.

Approach I ( Brute Force )

Algorithm / Steps

1. Create two variables: a boolean flag and an integer sum.
    
2. while i < size, traverse the array
   
   
   • While j<size, traverse the second array
      
   • If the i’th element is present in the second array
      
   • Return false
      
3. Return true

Time Complexity

O(N*N): Where ‘N’ is the length of the array.

Reason: The worst-case scenario is when we are checking for each element in another array.

Auxiliary Space Complexity 

O(1): Constant Space

Reason: No Additional space is required.

Approach II ( Hashing )

We are given two sets, presuming that both sets are already sorted, and we compare the elements in the two sets. If there is a match, the set is not disjoint; if there is no match, the set is disjoint. 

Algorithm / Steps

Let’s quickly walk through the algorithm for the Check If Two Given Sets Are Disjoint problem:

1. Make a hash table.
    
2. Go through the first set several times and add each element to the hash table.
    
3. Check to see if any elements are present in the hash table as you iterate over the second batch. Returns false if the element is present; else, disregard it.
    
4. Return true if none of the second set's elements are found in the hash table.

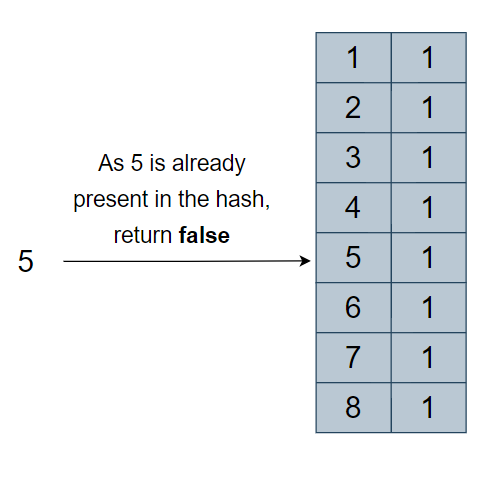
Algorithm Walkthrough

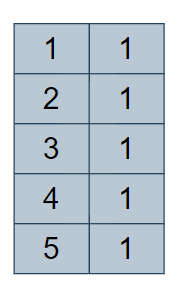
• After creating a map we’ll iterate through the array, 

• And store each element in the map after checking whether the element is present on the map or not,

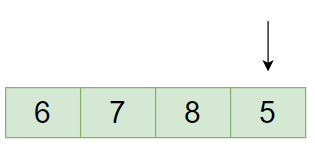
• If the element is present already on the map; return false.

Implementation in C++

Solution of the problem Check If Two Given Sets Are Disjoint in C++.

#include<bits/stdc++.h>
using namespace std;

bool checkDisjoint(vector<int> setA, vector<int> setB, int n1, int n2) {
	/* Creates an empty hashset using set */
	set<int> myset;
	
	/* traverse the first set, then hash its components. */
	for (int i = 0; i < n1; i++)
		myset.insert(setA[i]);
		
	/* Check the second set and determine whether any of its elements have already been hashed or not. */
	for(int i = 0; i < n2; i++)
		if (myset.find(setB[i]) != myset.end())
			return false;
			
	return true;
}

int main() {
	vector<int> setA{1, 2, 3, 4, 5};
	vector<int> setB{6, 7, 9, 5};
	
	if (checkDisjoint(setA, setB, setA.size(), setB.size()))
		cout << "Disjoint";
	else
		cout << "Not Disjoint";
}

Output:

Implementation in Java

Solution of the problem Check If Two Given Sets Are Disjoint in Java

import java.util.*;

public class HelloWorld {
	static boolean checkDisjoint(int set1[], int set2[]) {
		/* Creates an empty hashset using set */
		HashSet<Integer> set = new HashSet<>();
		
		/* traverse the first set, then hash its components. */
		for (int i=0; i<set1.length; i++)
			set.add(set1[i]);
			
	    /* Check the second set & determine whether any of its elements have already been hashed or not. */
		for (int i=0; i<set2.length; i++)
			if (set.contains(set2[i]))
				return false;
				
		return true;
	}
	public static void main (String[] args) {
		int set1[] = {1, 2, 3, 4, 5};
		int set2[] = {9, 6, 7, 8};
		
		if (checkDisjoint(set1, set2))
			System.out.println("A Disjoint Set");
		else
			System.out.println("Not Disjoint Set");
	}
}

Output:

Implementation in Python

Solution of the problem Check If Two Given Sets Are Disjoint in Python.

def checkDisjoint(set1, set2, n1, n2):
    # Creates an empty hashset
    myset = set([])
    
    # Traverse the first set and store its elements in hash
    for i in range (n1):
    	myset.add(set1[i])
    	
    # Traverse the second set and check if any element of it is already in hash or not.
    for i in range (n2):
    	if (set2[i] in myset):
        	return False
    return True

if __name__ == "__main__":
    set1 = [1, 2, 3, 4, 5]
    set2 = [6, 7, 8, 3]
    n1 = len(set1)
    n2 = len(set2)
    
    if (checkDisjoint(set1, set2, n1, n2)):
    	print ("Disjoint Set")
    else:
    	print("Not a Disjoint Set")

Output:

Time Complexity 

O(M+N): Where ‘M’&’N’ stands for the length of the array as provided in the problem statement of the Check If Two Given Sets Are Disjoint.

Reason: As we are iterating through both input arrays once, assuming methods of HashSet are working in O(1) time.

Auxiliary Space Complexity 

O(M+N): Where ‘M’&’N’ stands for the length of the array as provided in the problem statement of the Check If Two Given Sets Are Disjoint.

Reason: The worst-case scenario is when every element is unique, thus assigning space for each element.

You can also read about the Longest Consecutive Sequence.

Frequently Asked Questions

What does a disjoint set mean?

The term "disjoint sets" refers to a pair of sets that do not share any elements.

What are the various names of Disjoint Set Data Structures?

The union-find data structure and merge-find set are other names for the disjoint set data structure.

Are mutually exclusive and disjoint the same thing?

Events that never occur at the same moment are referred to as disjoint events. These are also referred to as occurrences that cannot coexist.

What does disjoint set rank mean?

Not the number of nodes in the tree, but its depth is represented by rank. The overall rank stays the same when two trees with different ranks are joined together.

What does a disjoint set in an algorithm mean?

A disjoint-set data structure is a type of data structure that organizes a set of components into various distinct (non-overlapping) subsets.

Conclusion

This article has gone through problems related to Hashing, we have discussed the question: Check If Two Given Sets Are Disjoint in multiple languages. To master the topic, check out some of our resources about hashmap, HashMap Implementation, and Introduction to HashMap.

Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations. Check out our articles in Library. You may also check out our course on the array.
Do upvote our blog to help other ninjas grow.
Happy Learning!