Introduction
This article will discuss the problem of checking whether the two trees are mirrors of each other or not. There is a prerequisite to solving this problem. You need to understand traversal in the binary tree. You can refer to this blog on coding ninjas to learn more about this.
Problem Statement
The problem states that we are given a root of the two binary trees, and we need to check if the two trees are mirrors of each other. Make a function that will return true if two trees are mirrors of each other.
See the sample example for a better understanding of the question.
Sample Examples
Input:
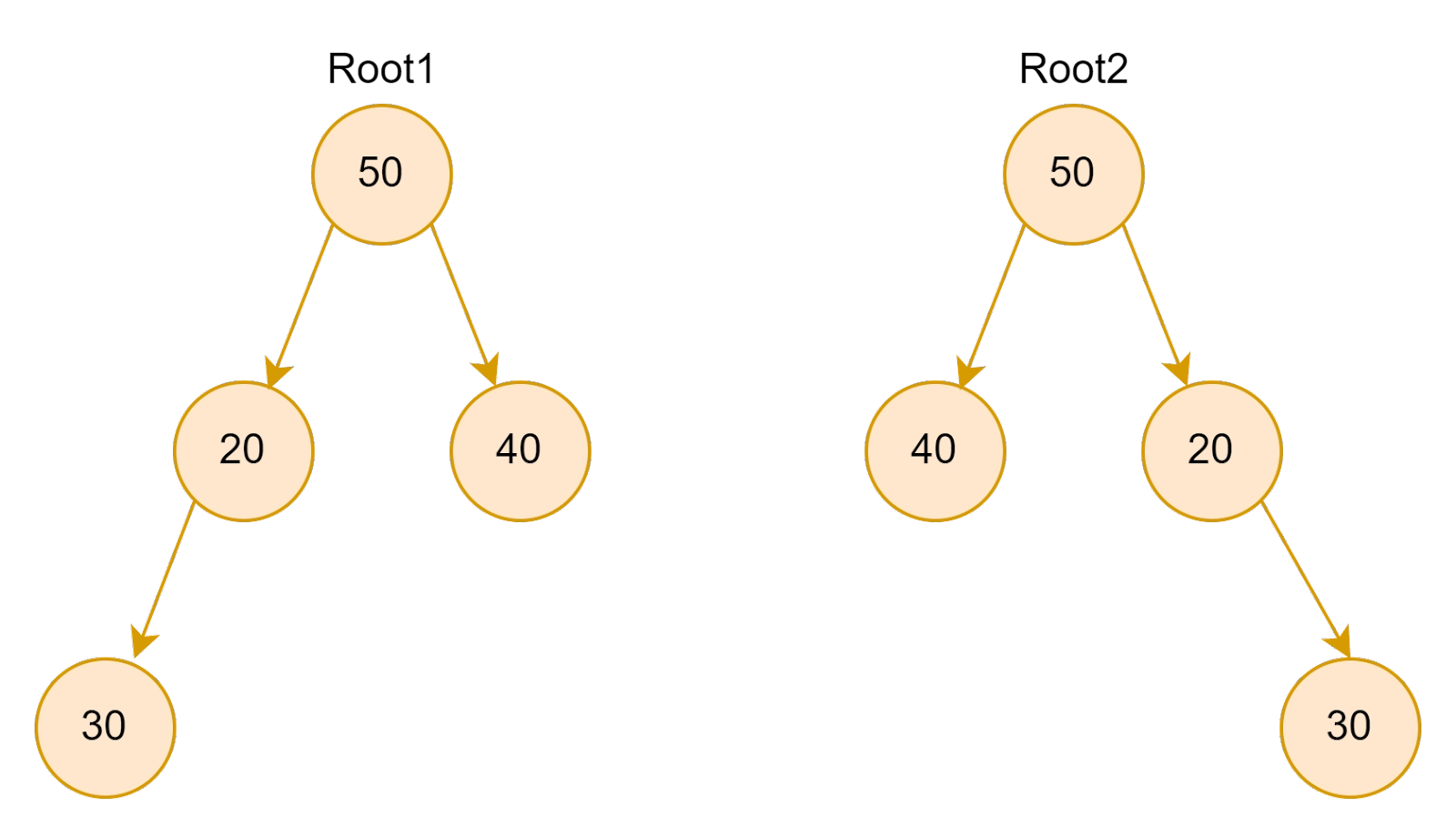
Output: True
Explanation: These two trees are mirror images of each other, as the left subtree of root1 is the same as the right subtree of root 2.
Input:
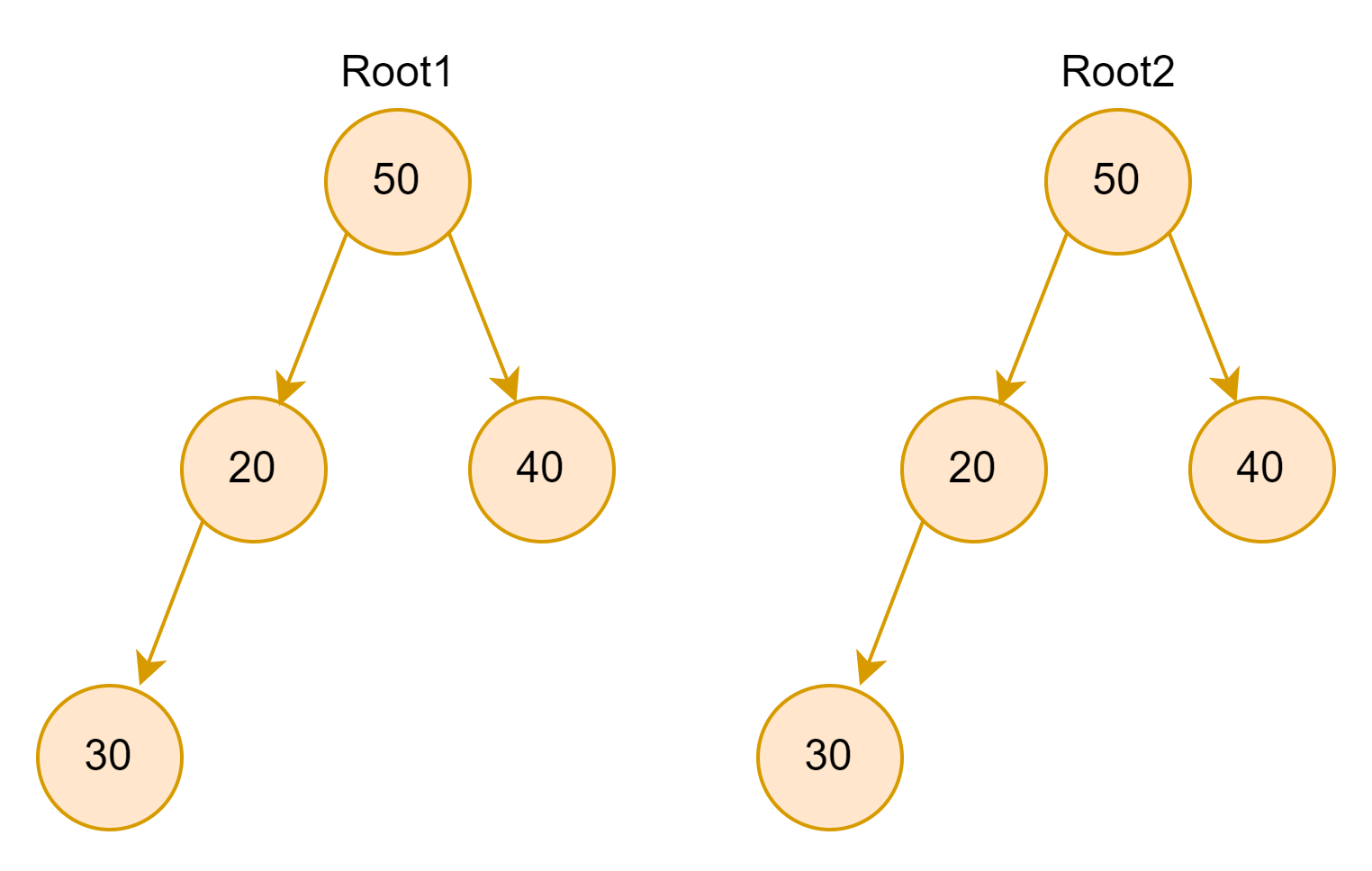
Output: False
Explanation: root1 left subtree is not the same as root2 right subtree, therefore they do not mirror images of each other.
Solution Approach
The idea is very simple, we recursively traverse for the left subtree of root1 and right subtree of root2, then the right subtree of root1 and left subtree of root2, and check for each node, that value of root->key must be the same.
Algorithm
- Take the input of the binary tree.
- Pass the root1 and root2 of binary trees to function, checkMirror(root1, root2).
- Now check the node value in both the trees; if they are not the same, return false.
- Now recursively call for the left subtree of root1 and right subtree of root2.
- Then make the recursive call for the right subtree of root1 and left subtree of root2.
- There are 2 base conditions, if both the tree becomes NULL, then return true; otherwise, if one tree is NULL, and another tree is not NULL, then return false.
C++ Code
// C++ code to check if two trees are mirror
#include <bits/stdc++.h>
using namespace std;
class TreeNode
{
public:
TreeNode *left, *right;
int val;
TreeNode(int val)
{
this->val = val;
this->left = NULL;
this->right = NULL;
}
};
// function to check if two trees are mirror
bool isMirror(TreeNode *root1, TreeNode *root2)
{
// if both the trees are NULL, return true
if (!root1 && !root2)
return true;
// if one is null, other is not null
if (!root1 || !root2)
return false;
bool left = isMirror(root1->left, root2->right);
bool right = isMirror(root1->right, root2->left);
// if we get true from both the sides, and the value of nodes are also same,
// return true
if (left && right && root1->val == root2->val)
return true;
// else return false;
return false;
}
int main()
{
// constructing the tree 1
TreeNode *root1 = new TreeNode(50);
root1->left = new TreeNode(20);
root1->left->left = new TreeNode(30);
root1->right = new TreeNode(40);
// constructing the tree 2
TreeNode *root2 = new TreeNode(50);
root2->left = new TreeNode(40);
root2->right = new TreeNode(20);
root2->right->right = new TreeNode(30);
// calling the function to check if two trees are mirror
if (isMirror(root1, root2))
{
cout << "Trees are mirror of each other" << endl;
}
else
{
cout << "Trees are not mirror of each other" << endl;
}
}Output
Trees are mirrors of each otherTime Complexity: O(N)
We are only doing linear traversal of the tree, so to check if two trees are mirrors, is O(N).
Space Complexity: O(1)
We are not taking any extra space.
Check out this problem - Mirror A Binary Tree.