Introduction
Today, We will discuss the Evergreen topic of DSA., i.e., Binary Tree. Do you want to learn that cream question and be a ninja? Just follow this blog.
We will see a Problem on the Full Binary Tree. Before that, we will have some insights about the Full Binary Tree.
Full Binary Tree
A Full Binary Tree is a special binary tree in which every node has either two or no child. It is also known as a proper binary tree.
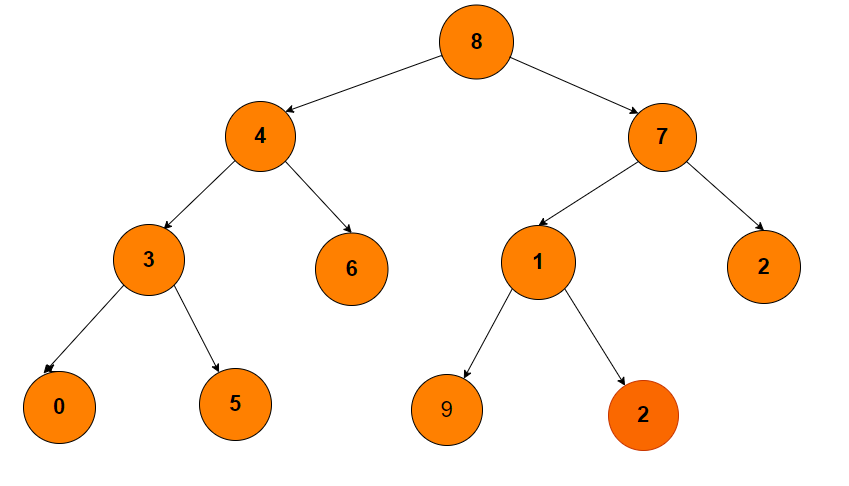
Problem Statement
Given a Binary Tree, You have to tell Whether the given Binary Tree is a Full Binary Tree or Not.
Sample Example
Input:
In Input, we have been given a Binary Tree as shown in the above figure, and we need to determine if it's a full binary tree or not.
Output:
The Given Tree is Full Binary Tree.
Explanation:
As you can see in the tree that all the nodes in the tree have either 0 or 2 nodes. So, this tree is Full Binary Tree. Approach
It is a Recursive Approach. Basically, we have to traverse the tree and For every Node, we have to find out whether any node has one node.If all the Node in the Binary Tree has either Zero or Two Node, then the tree is Full Binary Tree.
Steps of Algorithm
Before going through the steps of algorithms, you should see about '&&' operator operating between
Step 1. Create a Boolean Function IsFullBinaryTree, which takes the tree's root node.
Step 2. If the Binary Tree is Not Formed(Empty) means Root is NULL, then return Root Node.
Step 3. If Any Node is Leaf Node, then Return True.(Base Case)
Step 4. If the Particular Node has left and right child, then we recursively check for its left and right Subtree and return the Output.
Step 5. Except above points , For all combinations of right and left sub-trees, the Given Tree is not a Full Binary Tree.
Implementation in C++
// Program to check whether a Binary Tree is Full Binary Tree
#include <bits/stdc++.h>
using namespace std;
// Structure Of Node
struct Node
{
int key;
struct Node *left;
struct Node *right;
};
// Creation of New Node
Node *newNode(int key)
{
Node *node = new Node;
node->key = key;
node->left = node->right = NULL;
return (node);
}
// Checking whether a Tree is Full Binary Tree or Not.
bool IsBinaryTreeFull(struct Node *root)
{
// If Root Node is Empty then return True.
if (root == NULL)
return true;
// If Node is a Leaf Node means left child and right node is NULL
if (root->left == NULL && root->right == NULL)
return true;
// If Left Node and Right Node are not NULL then make a Recursive Call for Left Node And Right Node.
if ((root->left) && (root->right))
return (IsBinaryTreeFull(root->left) && IsBinaryTreeFull(root->right));
// Means At End,The Node has Only 1 child(Either Left Child or Right Child) return False.
return false;
}
int main()
{
struct Node *root = NULL;
root = newNode(8);
root->left = newNode(4);
root->right = newNode(7);
root->left->left = newNode(3);
root->left->right = newNode(6);
root->right->left = newNode(1);
root->right->right = newNode(2);
root->left->left->left = newNode(0);
root->left->left->right = newNode(5);
root->right->left->left = newNode(9);
root->right->left->right = newNode(2);
if (IsBinaryTreeFull(root))
cout << "The Given Tree is Full Binary Tree ";
else
cout << "The Given Tree is Not Full Binary Tree";
return 0;
}
Output:
The Given Tree is a Full Binary Tree.
Implementation in Java
// Checking if a binary tree is a full binary tree in Java
// Structure and Formation Of Node
class Node
{
int data;
Node LeftChild, RightChild;
Node(int item)
{
data = item;
LeftChild = RightChild = null;
}
}
public class BinaryTree
{
Node root;
// Checking whether a Tree is Full Binary Tree or Not.
boolean IsBinaryTreeFull(Node node)
{
// If Root Node is Empty then return True.
if (node == null)
return true;
// If Node is a Leaf Node means left child and right node is NULL
if (node.LeftChild == null && node.RightChild == null)
return true;
// If Left Node and Right Node are not NULL then make a Recursive Call for Left Node And Right Node.
if ((node.LeftChild != null) && (node.RightChild != null))
return IsBinaryTreeFull(node.LeftChild) && IsBinaryTreeFull(node.RightChild);
// Means At End,The Node has Only 1 child(Either Left Child or Right Child) return False.
return false;
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(8);
tree.root.LeftChild = new Node(4);
tree.root.RightChild = new Node(7);
tree.root.LeftChild.LeftChild = new Node(3);
tree.root.LeftChild.RightChild = new Node(6);
tree.root.RightChild.LeftChild = new Node(1);
tree.root.RightChild.RightChild = new Node(2);
tree.root.LeftChild.LeftChild.LeftChild = new Node(0);
tree.root.LeftChild.LeftChild.RightChild = new Node(5);
tree.root.RightChild.LeftChild.LeftChild = new Node(9);
tree.root.RightChild.LeftChild.RightChild = new Node(2);
if (tree.IsBinaryTreeFull(tree.root))
System.out.print("The Given Tree is Full Binary Tree");
else
System.out.print("The Given Tree is Not Full Binary Tree");
}
}
Output:
The Given Tree is a Full Binary Tree.
Complexity Analysis
Time complexity
O(n), where n is the number of nodes in a tree. As we are only traversing the Binary Tree using recursion, Hence The Time complexity of this algorithm is O(n).
Space complexity
O(n), As recursive Procedure uses stack takes O(n) space.
Check out this problem - Mirror A Binary Tree
Must Read Recursion in Data Structure




