Approach
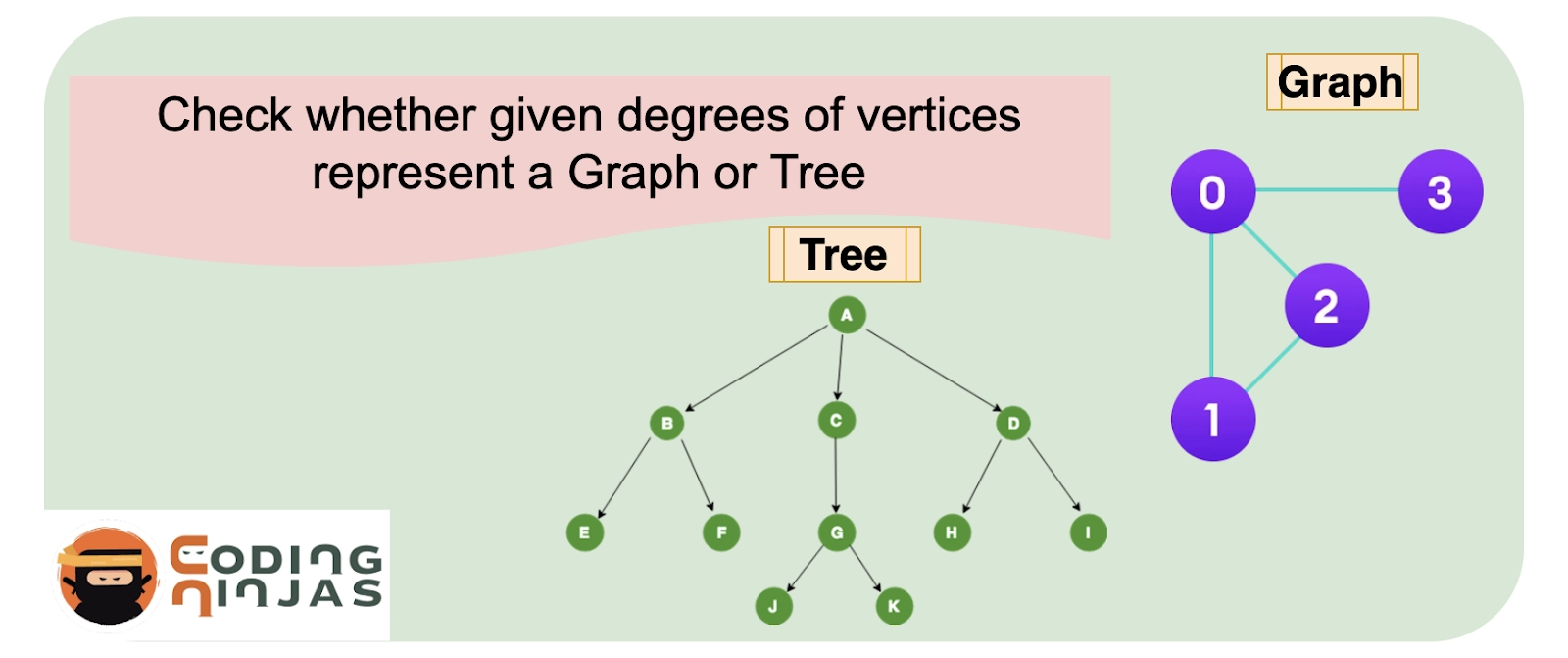
The number of edges entering or exiting a vertex determines its degree. The characteristics of trees make it easy to accomplish this.
-
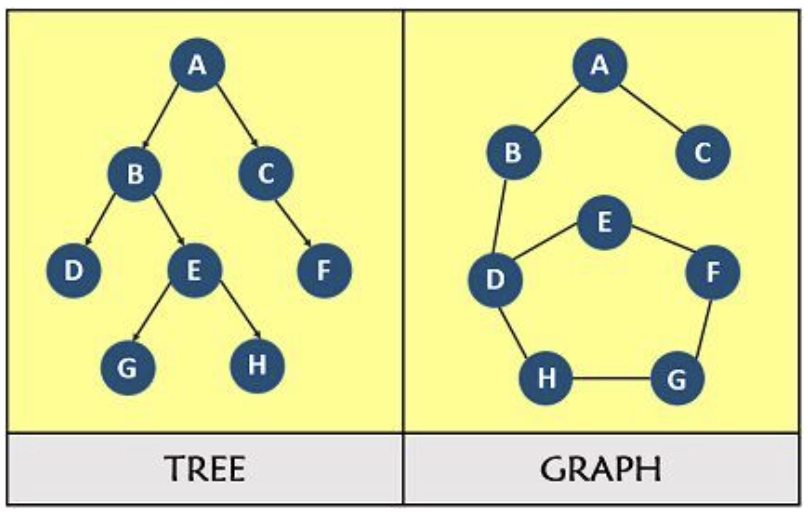
While graphs can contain cycles, trees are connected and do not.
-
There is no such restriction for a graph, but a tree has exactly n-1 edges.
-
The input graph is taken to be connected. It takes at least n-1 edges to connect n nodes. Each edge will be tallied twice if all the degrees are added.
If we add all the degrees, each edge will be counted twice. As a result, The total of all degrees for a tree with n vertices and n - 1 edge should equal 2 *(n – 1). For further information, please see Handshaking Lemma.
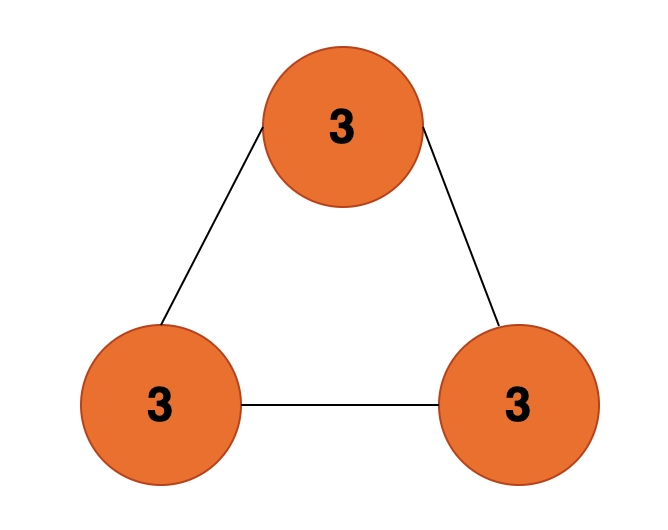
In essence, we must determine whether the sum of all degrees is 2*(n-1) or not.
Implementation in C++
// Checks whether the input degree sequence is a graph or a tree in C++.
#include<iostream>
using namespace std;
// The function returns either true for trees or false for graphs.
bool check(int degree[], int n)
{
// Fetching sum of all degrees
int sum = 0;
for (int i = 0; i < n; i++)
sum += degree[i];
// If the sum is 2(n-1), the graph is a tree
return (2*(n-1) == sum);
}
// programme for testing the above functionality
int main()
{
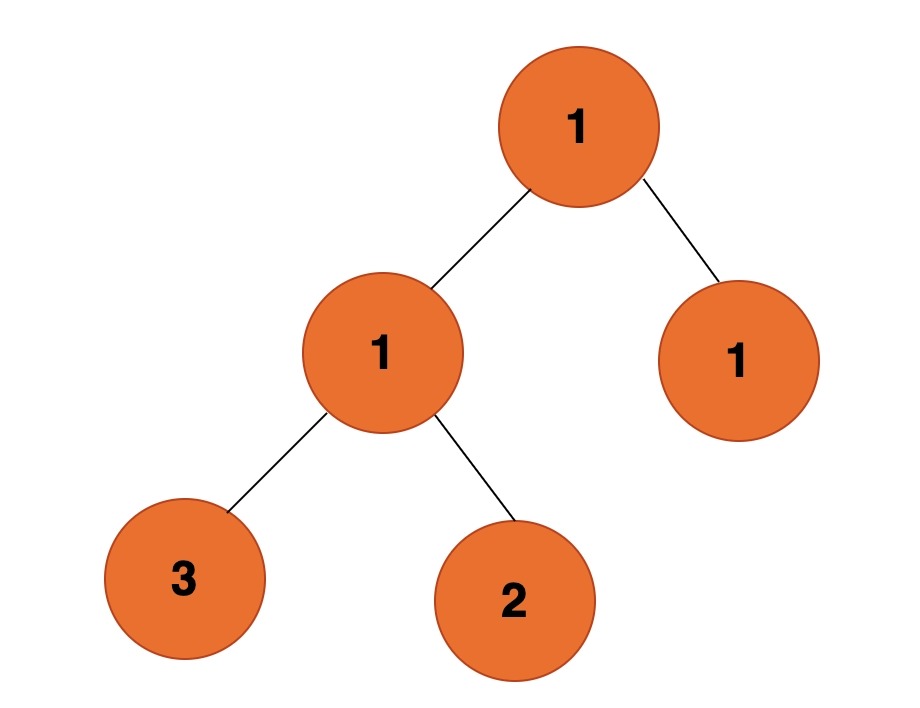
int n = 5;
int degree[] = {1, 1, 1, 3, 2};
if (check(degree, n))
cout << "Tree";
else
cout << "Graph";
return 0;
}
Output
Tree
Implementation in Java
// Checks whether the input degree sequence is a graph or a tree in java.
class Fetch
{
// The function returns either true for trees or false for graphs.
static boolean check(int degree[], int n)
{
// Fetching sum of all degrees
int sum = 0;
for (int i = 0; i < n; i++)
{
sum += degree[i];
}
// If the sum is 2(n-1), the graph is a tree
return (2 * (n - 1) == sum);
}
// programme for testing the above functionality
public static void main(String[] args)
{
int n = 5;
int degree[] = {1, 1, 1, 3, 2};
if (check(degree, n))
{
System.out.println("Tree");
}
else
{
System.out.println("Graph");
}
}
}
Output
Tree
Implementation in Python
# Checks whether the input degree sequence is a graph or a tree in C++.
def check(degree, n):
# Fetching sum of all degrees
sum = sum(degree)
# If the sum is 2(n-1), the graph is a tree
if (2*(n-1) == sum):
return True
else:
return False
#programme for testing the above functionality
n = 5
degree = [1, 1, 1, 3, 2];
if (check(degree, n)):
print "Tree"
else:
print "Graph"
Output
Tree
Complexity
Time Complexity
O(N): where n is the size of array.
Reason: As we are fetching the sum of degrees in the program so, we are using for loop, which iterates from 0 to n.
Space complexity
O(N): where n is the size of array.
Reason: As we are fetching the sum of degrees in the program so, we are using for loop, which requires an array of size n.
Check out this problem - Largest BST In Binary Tree
Frequently Asked Questions
What specific point distinguishes a tree from a graph?
There are vertices/nodes and edges in a graph. There are many nodes and edges in a tree. There is no single node in the graph that is the root. There is a special node in a tree called the root.
What are storage structures for graphs?
A graph is a type of data structure where information is stored among numerous groups of connected edges (paths) and vertices (nodes). Many Nodes and Edges make up the graph data structure. Vertices and nodes must both be finite.
What use cases does graph DS have?
Application in defining the software applications' computational flow. It is used to create transportation systems in Google Maps. In Google Maps, the node is the intersection of two or more roads, and the edge is the route that connects two nodes.
What purpose do graph algorithms serve?
In order to depict graphs as networks, such as flights, the Internet's connectivity, or Facebook's social network connectedness, graph algorithms are utilised. They are frequently used to create networks in NLP and machine learning.
What is a tree, and what is its type?
A particular kind of data structure used to represent hierarchical data is a tree. Nodes and edges make up the nonlinear structure. The complexity rises with the size of the data for the different kinds of data structures that carry out operations in a linear data structure.
Conclusion
We have checked whether given degrees of vertices represent a Graph or Tree by implementation with three different programming languages. If you want to master Graph and Tree, please check the following articles:
If you face any doubt, please comment, and we will love to answer your questions.
Want expertise in Python for your next web development project? Check out our course.
Nevertheless, you may consider our paid courses to give your career an edge over others!
Do upvote our blogs if you find them helpful and engaging!
Happy Learning!