Introduction
In this problem, we need to check whether the length of our linked list is odd or even. There are various approaches to solve this problem. We will cover some of them here. So let us dig deeper into this problem statement as well as the solution.
Recommended Topic, Floyds Algorithm
Problem Statement
In this problem, we are given a linked list and should evaluate its length (count the number of nodes in the linked list) and whether it is Even or Odd.
The term 'even' indicates that the linked list has an even number of nodes.
The term 'odd' indicates that the number of nodes in the linked list is odd.
Let us understand this problem statement with the help of an example.
Sample Example
Given is a linked list below. We have to count the total number of nodes and decide whether it is even or odd.
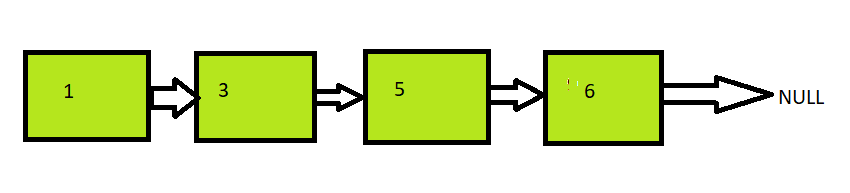
The following is the output of the above input: Even (since the count of the total number of nodes is 4 and 4 % 2 is equal to 0).
We simply have to count the total node in the list and determine whether it is odd or even. In the above test case, for example, the total number of nodes in the list is 4, and 4 is an even number, so the output is 'Even'. The output would have been 'Odd' if the number of nodes had been an odd number.

Source: linked list
Approach 1: Brute force approach
This approach is very simple to implement and straightforward. In this approach, we simply count the total number of nodes in the linked list by iterating the given list and printing the output based on whether the count is odd or even.
Let us see its algorithm.
Steps of Algorithm
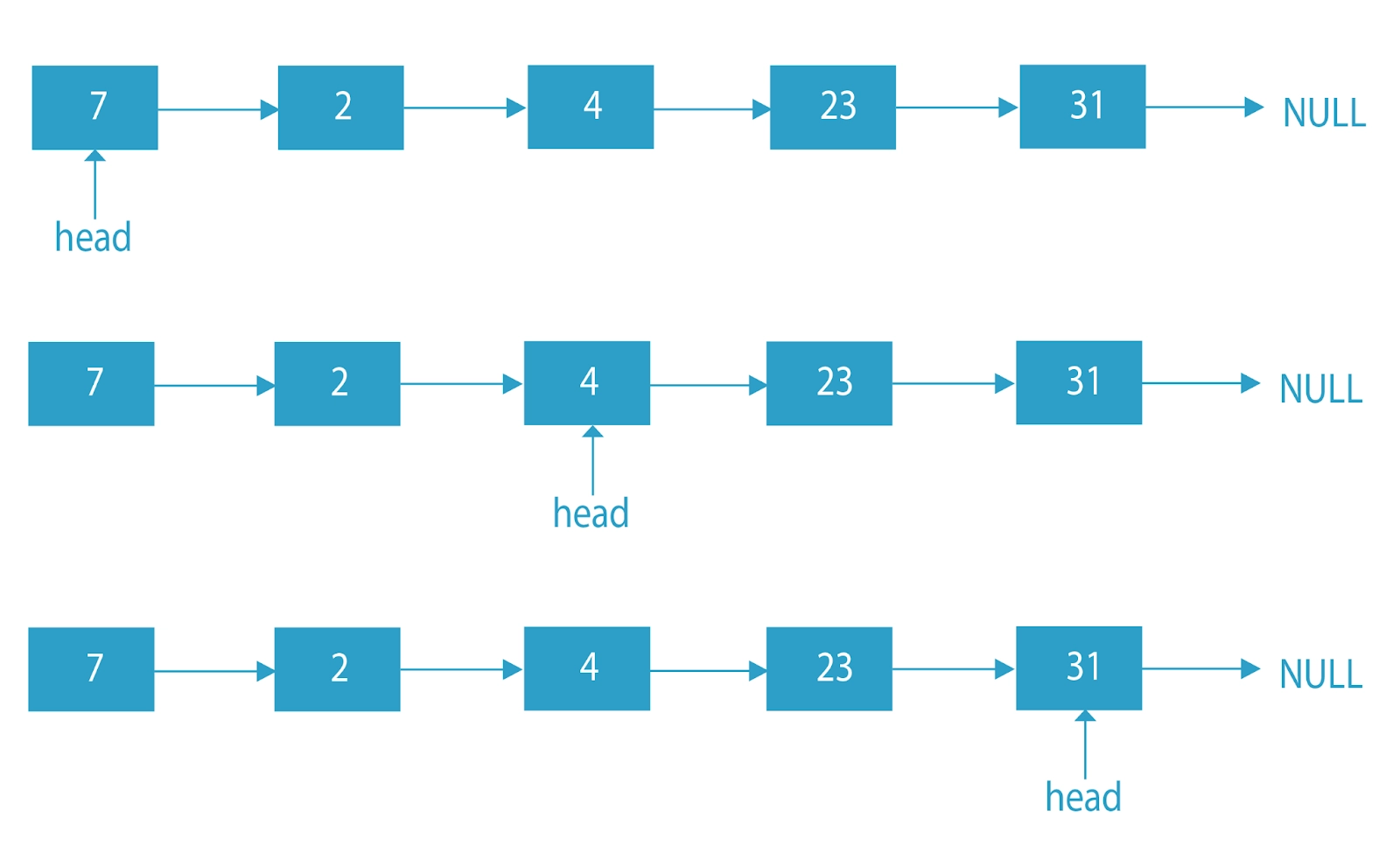
Step 1: Create a temporary pointer and a variable named- length. Set the pointer to the very first node of the linked list and initialize length = 0.
Step 2: Begin iterating through the linked list, and with the traversal of every node, increase the value of length with each valid node.
Step 3: Variable length will give us the length of the linked list after iteration. We just need to calculate the length value. I.e. if (length % 2 == 0), the linked list is of even length.
And if length % 2 == 1), the linked list is of odd length.
Let us understand this approach with the help of a diagram.

In this linked list, we will create a variable-length = 0. After traversing the whole linked list, we will get the value of length = 6. And after calculating its mod with 2. We will get to know that the linked list is of even length.
Pseudocode
bool even_odd_length(struct node* link_list){
int length=0; // Counter to keep the track of the length of the linked list.
while(link_list){ // Iterate the linked list.
link_list=link_list->next;
length=length+1; // increment the counter with every node visited.
}
if(length%2==0){ // Length even, return true
return true;
}else{
return false;
}
}
Let us see the implementation of this approach in the next section of this blog.
Implementation in C++
#include<bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
bool is_length_even(Node* head)
{
int counter=0; // Counter to keep the track of the length of the linked list.
while(head){ // Iterate the linked list.
head=head->next;
counter=counter+1; // increment the counter with every node visited.
}
if(counter%2==0){ // Length even, return true
return true;
}else{
return false;
}
}
int main()
{
Node* head = NULL;
head = new Node(10);
head->next = new Node(20);
head->next->next = new Node(40);
//head->next->next->next = new Node(60);
if(is_length_even(head)){ // Check whether the linked list has even length or odd.
cout<<"even length";
}else{
cout<<"odd length";
}
return 0;
}
Output:
odd length
Let us analyze the time and complexity of the above implementation.
Complexity analysis
Time complexity
As we have to traverse the linked list whole to know the length. So this approach will take O(N), where N is the total number of nodes in the linked list.
Space complexity
In this approach, we only need a pointer variable and an integer variable: length. So this will not cost any memory space. And it will take O(1).