Introduction
Combinatorics is an area of mathematics that deals with the selection, arrangement, and counting of collections of items. Combinatorics scope has grown to cover areas such as graph theory, number partitions, block designs, code design, and Latin squares. Combinatorics dates back over 3000 years and began as a study of permutations and combinations. Combinatorics: A Very Short Introduction gives a broad overview of the field and its applications in mathematics and computer science, covering topics such as the shortest routes between two points and the smallest number of colors required to draw a map with different colors for neighboring countries.
Question 1: How many reflexive relations can there be on a set of five elements?
- 2^5
- 2^10
- 2^15
- 2^20
Answer: D
Formula to calculate the number of reflexive relations is :
2^(n^2-n) which is 220 for n = 5
Question 2: How many different Boolean functions can you have with n Boolean variable
- 2^n
- 2^(2*n)
- 2^2^n
- n^2
Answer: C
For a variable Boolean function, the maximum number of input sequences feasible is = 2n
Each input sequence can give either T or F as output ( 2 possible values )
So, the Total no of Boolean functions is -
2X2X2X2X2X2X.............X2X2X2X2X2X2
<-------------------- 2n Times -------------->
2^2^n
Question 3: How many four-digit even numbers have 4 separate digits?
- 2296
- 2278
- 2256
- 2592
Answer: A
This is a basic question from the permutation combination in Combinatorics.
Consider two crucial cases :
numbers ending with 0 and not ending with 0.
Numbers ending with 0 1{first place: 0} ∗ 9{fourth place: 9 possibilities, 1-9} ∗ 8{third place: 8 possibilities left} ∗ 7{second place: 7 possibilities left} = 504
Numbers ending with non-0 4{first place: 2,4,6,8} ∗ 8{fourth place: 8 possibilities left, 1-9} ∗ 8{third place: 8 possibilities left b/w 0-9} ∗ 7{second place: 7 possibilities left b/w 0-9} = 2592
Total = 2296
Question 4:The number of four-digit numbers formed with digits in non-decreasing order (from left to right) using digits from the set {1, 2, 3} is
- 12
- 13
- 15
- 16
Answer: C
Below are all the possible sets
{1, 1, 1, 1} {1, 1, 1, 2} {1, 1, 1, 3} {1, 1, 2, 2} {1, 1, 2, 3} {1, 1, 3, 3} {1, 2, 2, 2} {1, 2, 2, 3} {1, 2, 3, 3} {1, 3, 3, 3} {2, 2, 2, 2} {2, 2, 2, 3} {2, 2, 3, 3} {2, 3, 3, 3} {3, 3, 3, 3}
Question 5: Two boys have picked 10 red balls, 15 blue balls, and 14 green balls. What is the total number of ways they can divide the balls amongst themselves?
- 2800
- 2164
- 2640
- 2558
Answer: C
Number of ways in which n identical or same things can be divided into r groups if blank groups are allowed (here groups are numbered, i.e., distinct) then
= Number of ways in which n identical things can be distributed among r persons, each one of them can receive 0,1,2 or more items is equal too
= (n+r-1)C(r-1)
can we do this here boys =2 Let these two boys are two groups, 10 red balls,
so (10 + 2 -1) C(2-1) = 11
and so on
Assume the two boys only have 10 red balls. They can share these in (11 choose 1) = 11C1 = 11 ways. Similarly, they can share 15 blue balls and 14 green balls in (15 choose 1) = 15C1 = 16 ways (14 choose 1) = 14C1 = 15 ways So, they can share all the balls in 11 * 16 * 15 = 2640 ways
Question 6: A dice is thrown. Let X be the event that the number obtained is greater than 5. Let Y be the event that the number obtained is less than 5. Then P (XUY) is
- ⅓
- ½
- ⅔
- ⅚
Answer: D
This Combinatorics question is from Probability. Since, X{6}, and Y{1, 2, 3, 4}. Therefore, X∩Y = {∅}. So, P(A∪B) = P(A)+P(B)-P(A∩B) = 1/6 + 4/6 - 0 = ⅚
Question 7:Find The total number of bit strings having length of 8 that will either start with 1 or end with 00 is?
- 32
- 160
- 92
- 144
Answer: B
(I) Number of 8 bit strings starting with 1 : 1 _ _ _ _ _ _ _ = 27 = 128 (II) Number of 8 bit strings ending with 00 : _ _ _ _ _ _ 00 It has 2 possibilities: if the string starts with 0 then total strings = 25 = 32 and if the string starts with 1 then total strings = 32 but they are already covered in all the strings starting with 1 So, the total number of strings = 128 + 32 = 160
Question 8: Let X be a sequence of 8 distinct integers sorted in sorted order. How many different pairs of sequences, Y and Z are there such that
(i) each are sorted in ascending order
(ii) Y has 5 and Z has 3 elements
(iii) the result of merging Y and Z gives X?
- 30
- 56
- 28
- 8
Answer: B
This Combinatorics is question from permutation and combinations.Imagine you have selected 3 elements out of 8 elements in 8C3 ways, the rest of the elements are treated as another array, and finally after merging both the arrays gives the sorted array. Now Here, you can select either 3 or 5.
=> 8C3 = 8C5 = 8!/(3!5!) = 7*8 = 56 Ways.
Question 9:For a set x, the power set of x is denoted by 2x. If x = {5, {6}, {7}}, which of the following options are True.
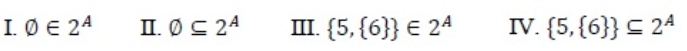
- I and III only
- II and III only
- I, II and IV only
- I, II and III only
Answer: D
x = {5, {6}, {7}}
Such types of questions are very common in Combinatorics where we need to make the entire power set.
Below is Powerset of x
{ φ,
{5},
{{6}},
{{7}},
{5, {6}},
{5, {7}},
{{6}, {7}},
{5, {6}, {7}}
}
Ans I is true because φ belongs to the Powerset generated. II is also true, as we know that an empty set is a subset of every possible set. III is also true as {5, {6}} belongs to Powerset generated but IV is not true because {5, {6}} is not a subset, but {{5, {6}}} is a subset.
Question 10: The number of arrangements of six identical socks in three identical cupboards is
- 32
- 28
- 42
- 20
Answer: B
No of ways = (6+3−1)C3−1 = 28
Key Takeaways
In this article, we have extensively discussed the important questions from the Combinatorics and some previously asked questions in the gate exam.
Until then, All the best for your future endeavors, and Keep Coding. "We hope that this blog has helped you enhance your knowledge regarding this problem, and if you would like to learn more, check out our articles on Coding Ninjas Studio. Do upvote our blog to help other ninjas grow. Happy Coding!”




