Introduction
Combinatorics means the number of ways we can arrange some objects or we can choose some objects from a collection. It is one of the fundamental concepts that we need to know to solve programming problems. Here we will be discussing some basic formats of combinatorics problems and how to solve them. We will also implement the solutions of combinatorics problems in terms of pseudocode.
Principles of Combinatorics
Sum rule:
If there are n1 number of ways to reach the destination B from A and n2 number of ways to reach destination C from B, then there are total n1+n2 number of ways to reach destination B or C.
Example
You need to travel in between city A and B. You can either fly, take a train, or a bus. There are 12 different flights in between A and B, 5 different trains and 10 buses. How many options do you have to get from A to B?
Ans.
According to the sum rule, there are total (12+5+10)=27 options to get from A to B.
Product rule:
If there are n1 number of ways to reach the destination B from A and n2 number of ways to reach destination C from B, then there are total n1*n2 number of ways to reach from A to destination C.
Example
A new company with just two employees, Dhruv and Souhard, rents a floor of a building with 12 offices. How many ways are there to assign different offices to these two employees?
Ans. Dhruv can be assigned with an office in 12 ways, and Souhard can be assigned with any one of the remaining 11 offices after assigning Dhruv with one. So, by product rule, there are 12*11=132 ways to assign different offices to these two employees.
The Subtraction Rule (Inclusion-Exclusion Principle)
It uses a sum rule and then corrects for the overlapping part i.e., If a task can be done in either n1 ways or n2 ways, then the number of ways to do the task is n1 + n2 minus the number of ways to do the task that are common to the two different ways.
Example
How many bit strings of length 5 start either with a bit 1 or end with 0?
Ans.
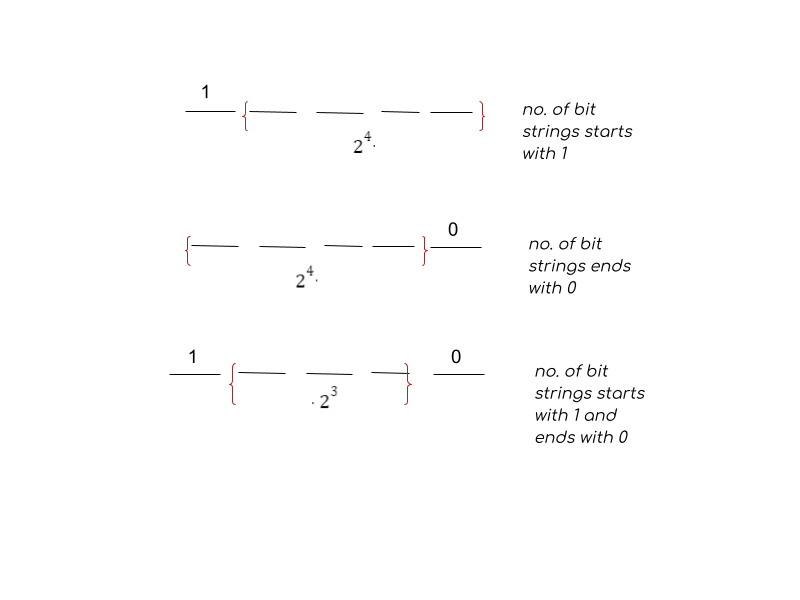
(no. of bit strings starts with 1 + no. of bit strings ends with 0) – no. of bit strings starts with 1 and ends with 0)
=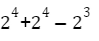
Pigeonhole Principle
If k + 1 or more objects are placed into k boxes, there is at least one box containing two or more of the objects where k is a positive integer.
There are 13 pigeons sitting in 12 holes. So, there is at least one hole where 2 or more pigeons are sitting in every possible arrangement.
Example
In any group of 27 English words, there must be at least two that begin with the same letter because there are 26 letters in the English alphabet.
Note: Please try to solve the problems first and then see the below solution approaches.