Introduction
Computer arithmetic is a branch of computer science that studies how computers should represent and manipulate numbers.
In this article, we will go through some crucial previous year questions of the GATE exam on the topic of Computer Arithmetic.
Questions
1. In IEEE single-precision floating-point encoding, the decimal value 0.5 has
(A) fraction bits of 000...000 and an exponent value of 0
(B) fraction bits of 000...000 and an exponent value of 1.
(C) 100...000 fraction bits and a value of 0 for the exponent
(D) there is no perfect representation
Answer: (B)
Explanation: The IEEE 754 standard specifies the following bit distribution:
1 bit for sign
8-bit exponent width
24 as a significand or fraction (23 explicitly stored)
In base 10, 0.5 equals 1 X 2-1 in base 2.
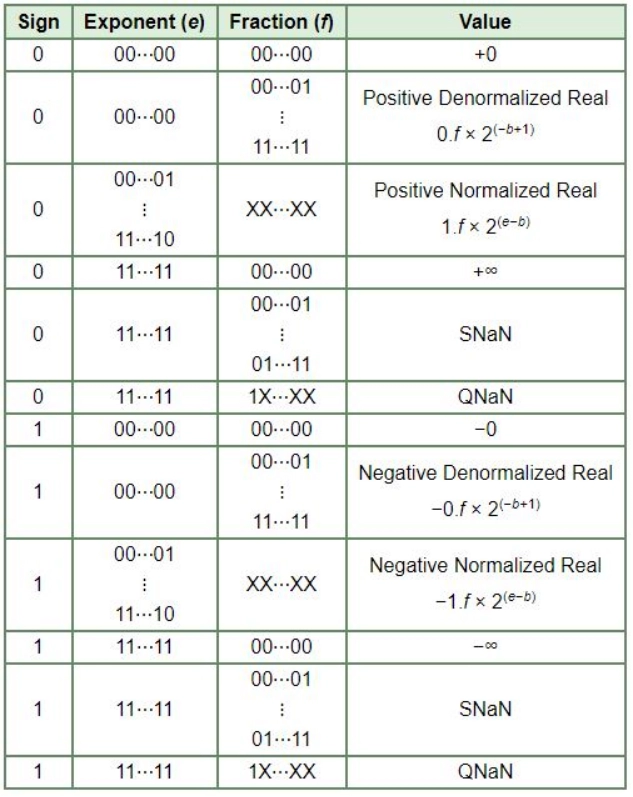
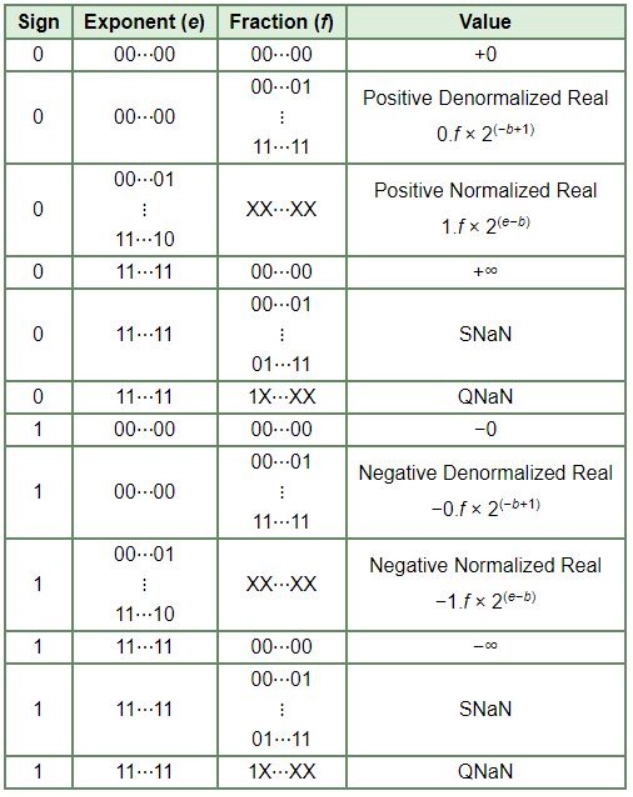
2. In the IEEE floating-point encoding, the hexadecimal value 0 00000000 corresponds to
(A) the normalized value 2^-127
(B) the normalized value 2^-126.
(C) the normalized value +0
(D) the special value +0
Answer: D
Explanation: Refer to the image below
3. What is the outcome of evaluating the two expressions below using three-digit floating-point arithmetic with rounding?
(113. + -111.) + 7.51
113. + (-111. + 7.51)
(A) 9.51 and 10.0
(B) 10.0 and 9.51
(C) 9.51 and 9.51
(D) 10.0 and 10.0
Answer: B
Explanation: (113 - 111) + 7.51 = 2 + 7.51 = 9.51
(113. + -111.) + 7.51
= 113. + (-111. + 7.51)
= 113. - 103.
= 10 [The figure 103.49 is rounded to 103.0]
4. Overflow occurs in 2′s complement addition.
(A) This is marked when there is carry from sign bit addition.
(B) When a positive value is added to a negative value, it cannot occur.
(C) When the carries from the sign bit and the previous bit match, the flag is raised.
(D) None of the preceding
Answer: (B)
Explanation: Overflow never happens when a positive value and negative value are added.
5. An N-bit carry-lookahead adder, where N is a multiple of 4, makes use of ICs 74181 (4 bit ALU) and 74182 (8 bit ALU) ( 4 bit carry look-ahead generator).
The shortest addition time for this adder utilizing the best architecture is
(A) in proportion to N
(B) logN proportional
(C) Constant
(D) None of the above
Answer: (B)
Explanation: When N=64 bits.
If you want to build a 64-bit adder, you will need 16 4-bit ALU and 16 4-bit carry generators. At this point, there will be 16 carries that will ripple through these 16 ALU modules. To speed up the adder, we need to get rid of these 16 rippling carries, so we can use four 4-bit carry generators to generate these 16 carries. Now we only have four carries to ripple through, and we can use the same trick to minimize the rippling of these 4
As a result, we employed three levels of a four-bit carry generator, and the time required to add 64 bits will be proportional to three, or log4(64).
In general, it takes log4N time to add N – bits.
6. Booth's algorithm for integer multiplication performs the worst when the multiplier pattern is used
(A) 101010 ………1010
(B) 100000 ………0001
(C) 111111 ………1111
(D) 011111 ………1110
The answer is: (A)
Explanation: The worst-case scenario for a Booth's method implementation is when pairs of 01s or 10s frequently appear in the multiplier.
7. A float variable's value is expressed using the IEEE-754 single-precision 32-bit floating-point format, employing 1 bit for sign, 8 bits for the biassed exponent, and 23 for the mantissa. The decimal number 14.25 is given to a float type variable X. In hexadecimal notation, X is represented as
(A) C1640000H
(B) 416C0000H
(C) 41640000H
(D) C16C0000H
Answer: (A)
Explanation: Because No is a negative number, the S bit will be 1.
14.25 is equal to 1110.01 in binary.
Biased Exponent (Add 127): 1.11001 X 2 3 Normalize it: 1.11001 X 2 3 Biased Exponent (Add 127): 3 multiplied by 127 equals 130. (In binary 10000010)
110010.....0 Mantissa (Total 23 bits)
The following number is expressed in IEEE 754 single-precision format:
1 10000010 11001000000000000000000
In Hex (Group of Four bits) -
1100 0001 0110 0100 0000 0000 0000 0000
Num becomes: C1640000
8. The carry generate function Gi and the carry propagates function Pi for inputs Ai and Bi in a look-ahead carry generator is provided by:
Pi=Ai⊕Bi and Gi=AiBi
The phrases for the look-ahead carry adder's sum bit Si and carry bit Ci+1 are as follows:
Si=Pi⊕Ci and Ci+1=Gi+PiCi,
Where C0 represents the input carry. Consider a two-level logic look-ahead carry generator implementation. Assume that the carry generating circuit has access to all Pi and Gi and that the AND and OR gates can have any number of inputs. The number of AND gates and OR gates required to build the look-ahead carry generator for a 4-bit adder with outputs S3, S2, S1, S0, and C4 is:
A. 6,3
B. 10,4
C. 6,4
D. 10,5
Answer: (B)
Explanation: C1=G0+C0.P0
C2=G1+G0.P1+C0.P0.P1
C3=G2+G1.P2+G0.P1.P2+C0.P0.P1.P2
C4=G3+G2.P3+G1.P2.P3+G0.P1.P2.P3+C0.P0.P1.P2.P3
4 OR gates are required for C1, C2, C3, C4
· 1 AND gate for C1
· 2 AND gate for C2
· 3 AND gate for C3
· 4 AND gate for C4
· AND =10
· OR =4
9. When two three-bit values, a2a1a0 and b2b1b0, are combined, the function that represents the carry generate function is:
A. a2b2+a2a1b1+a2a1a0b0+a2a0b1b0+a1b2b1+a1a0b2b0+a0b2b1b0
B. a2b2+a2b1b0+a2a1b1b0+a1a0b2b1+a1a0b2+a1a0b2b0+a2a0b1b0
C. a2+b2+(a2⊕b2)(a1+b1+(a1⊕b1)+(a0+b0))
D. a2b2+(a2)’a1b1+(a2a1)’a0b0+a2a0(b1)’b0+a1(b2)’b1+(a1)’a0(b2)’b0+a0(b2b1)’b0
Answer: (A)
Explanation: c1=a0b0
c2=a1b1+a1c1+b1c1
c3=a2b2+a2c2+b2c2
=a2b2+a2a1b1+a2a1c1+a2b1c1+b2a1b1+b2a1c1+b2b1c1
=a2b2+a2a1b1+a2a1a0b0+a2b1a0b0+b2a1b1+b2a1a0b0+b2b1a0b0
Considering the carry in function cc, c1=a0b0+a0c+b0cc1=a0b0+a0c+b0c, but cc is missing in all options and hence ignored.
10. The information is provided below. Solve the issues and select the proper solution.
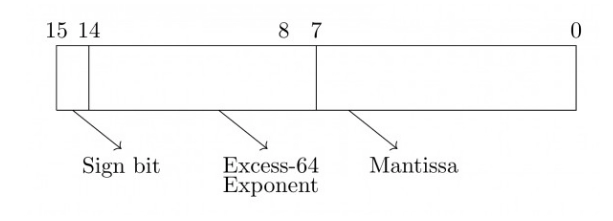
The following is the normalized representation for the format as mentioned earlier. The binary (radix) point is preceded by an implied 1 in the mantissa. Assume that when changing a field, only 0′s are padded in.
A. The normalized representation of the above number (0.239×213)(0.239×213) is:0A20
B. 1134
C. 49D0
D. 4AE8
Answer : (D)
Explanation: To find a normalized representation, we must first identify an unnormalized one. So far, we have:
The number is 0.239*2^13. As the capacity of the mantissa field is 8 bits, we can find the binary equivalent of 0.239 up to 8 bits.
We end here since we have completed 8 iterations and hence have 8 digits of unnormalized mantissa. We now have:
0011 1101 is the mantissa of the given number.
So, the number can be written as: 0.00111101×2^13
To obtain a normalized number, we must now align the mantissa to the left. In the query, it is stated that 0′s will be padded on the right side due to mantissa alignment to the left during the alignment procedure.
So, to produce a normalized number, we align to the left three times, yielding new mantissa =11101000.
Exponent will likewise reduce by three, resulting in a new exponent of ten.
As a result, normalized number=1.11101000210
The actual exponent is 10
Because an additional 64 is utilized, bias value =64.
As a result, the exponent field value is =10+64=74.
Of course, sign bit=0 denotes a positive integer.
As a result, the final representation of the number
=0100101011101000
=0100101011101000
=(4AE8)16
11. The data is given below. Solve the problems and choose the correct answer.
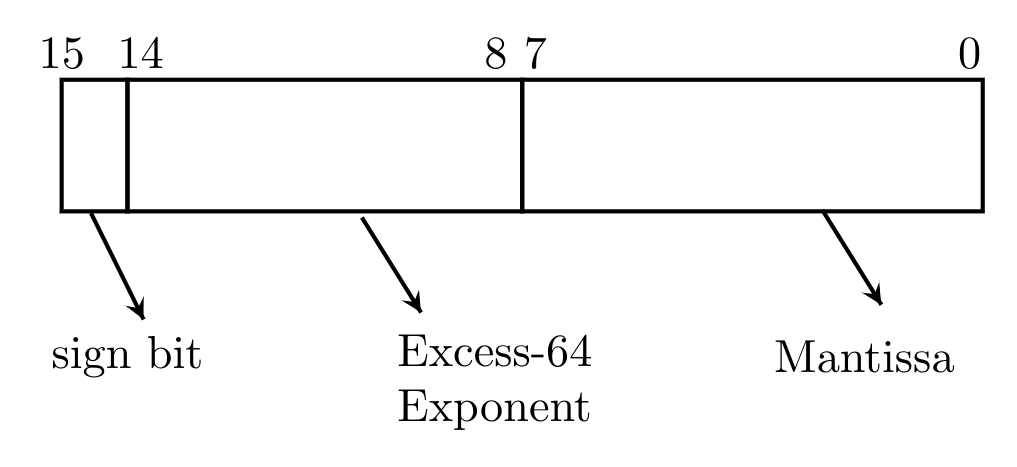
The mantissa is a pure fraction with signs and magnitude. Without normalizing or rounding off, the decimal number has the hexadecimal form shown below:
A. 0D 240D 24
B. 0D 4D0D 4D
C. 4D 0D4D 0D
D. 4D 3D
Answer: D
Explanation: Please refer to this image :
12. A 4-bit carry look-ahead adder is constructed using simply AND, OR, NOT, NAND, and NOR gates to add two 4-bit values. What is the overall propagation delay of the adder if all inputs are accessible in both complemented and uncomplemented versions and each gate's delay is a one-time unit? Assume the carry network is built with two levels of AND-OR logic.
A. 4-time units
B. 6-time units
C. 10-time units
D. 12-time units
Answer : (B)
Explanation:
It would take 6-time units to complete.
We already know that Gi=AiBi, Pi=AiBi, and Si=PiCi.
Also ,
C1=G0+P0C0
C2=G1+P1G0+P1P0C0
C3=G2+P2G1+P2P1G0+P2P1P0C0
C4=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C0
Level-1 ANDs and Level-2 ORs are the two levels of XOR. As a result, calculating Pi and Si would take two-time units.
The 4-bit addition will be computed in three phases.2 units of time in each stage. Thus, 6-time units.
13. The following is a strategy for representing floating-point numbers using 16 bits.

Let s, e, and m be the binary integers in the sign, exponent, and mantissa fields. Then the floating-point number is expressed as follows:

What is the greatest difference between two consecutive real numbers that may be represented in this system?
A. 2^−40
B. 2^−9
C. 2^22
D. 2^31
Answers: C
At extremes, the most significant difference between two consecutive real numbers will occur. This is due to the fact that numbers are represented up to mantissa bits, and as the exponent increases, the difference is multiplied by a bigger value. (The smallest change occurs for the least positive exponent value.)
14. The first step is to extend the sign.
(A) floating-point multiplication
(B) signed 16-bit integer addition
(C) arithmetic left shift
(D) converting a signed integer from one size to another
Answer: D
Explanation: Sign extension (filling the upper bits using the sign bit) is needed while increasing the number of bits for representing a number. For positive numbers, 00 is extended, and for negative numbers, 11 is extended.
15. Booth's 8-bit coding for the decimal number -57 is:
A. 0−100+1000
B. 0−100+100−1
C. 0−1+100−10+1
D. 00−10+100−1
Answer: B
Explanation :
Convert 57 to binary and get the complement of 2′s. It is "11000111" with an additional 0 to the right of it.
110001110
To find the booth code, subtract the right digit from the left digit in each successive two digits.
As a result, 110, 10+1, and finally, ten plus one.
16. To add 16-bit values, the number of full and half-adders necessary is:
A. 8 half-adders, 8 full-adders
B. 1 half-adder, 15 full-adders
C. 16 half-adders, 0 full-adders
D. 4 half-adders, 12 full-adders
Answer: B
Explanation: The correct answer is B.
We don't require a whole adder for LSB addition.
Because the carry from the previous addition must be passed into the addition operation, we require a complete adder every each bit addition.
17. Consider the following representation of a floating-point number:

The exponent is in 2’s complement representation, and the mantissa is in the sign-magnitude representation. The range of the magnitude of the normalized numbers in this representation is
a). 0 to 1
b). 0.5 to 1
c). 2^-23 to 0.5
d). 0.5 to (1-2^-23)
(A) a
(B) b
(C) c
(D) d
Answer: (D)
Explanation: If they had requested for Normalized mantissa instead of Normalized numbers, the method would have been as follows:
= 0.100 0000 0000 0000 0000 0000
= 1*2-1
= 0.5
And the maximum value of Mantissa=>
“S111 1111 1111 1111 1111 1111”
= 0.111 1111 1111 1111 1111 1111
= [(223)- 1] * 2-23
= 1-2-23
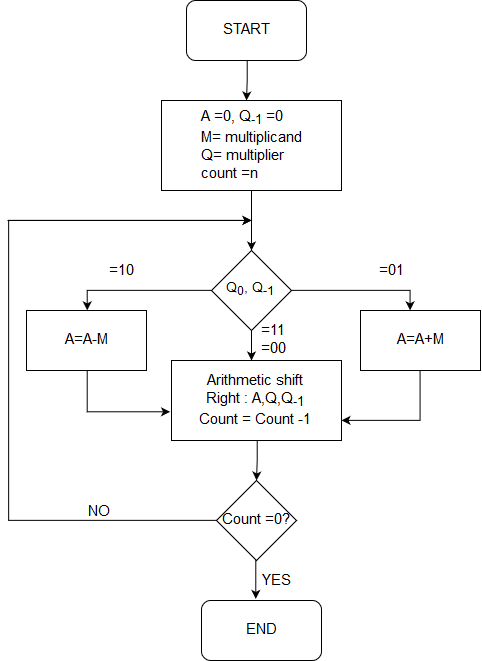
18. Explain Booth's algorithm for multiplying two integers. Create a block diagram of the Booth's algorithm for calculating the product of two 8-bit signed values.
Answer & Explanation :