Construct all possible BSTs for keys 1 to N

Approach

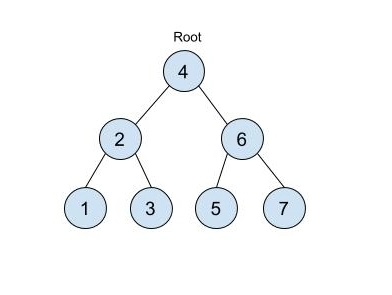
From the definition of a BST, it is clear that all nodes in the left subtree will be smaller than the root, and all the nodes in the right subtree will be greater than the root.

So, if we have a root node with the number i, then all the nodes in the left subtree will have values from the numbers 1 to i-1.

And all nodes in the right subtree will have values between the numbers i+1 to N.

If 1 to i-1 gives us x different subtrees and i+1 to N gives us y different subtrees, then with the ith number as root, we will have x*y total trees. We also have N choices for root.

So,

1. We will iterate from 1 to N for the root node.
2. We will run another loop for the left and right subtree.

Algorithm

1. Create and initialize the list BSTs as empty.
    
2. Run a for loop from 1 to N; for every number i, where i ranges from 1 and N, do the following:
   
   • With i as val, create a new node. Let this node be ‘newNode’.
   • Construct the list of all left subtrees recursively.
   • Construct the list of all right subtrees recursively.
      
3. Iterate over all left subtrees
   
   • Consider the current left subtree, and iterate over all right subtrees.
   • Now, add the current left and right subtree to ‘newNode’.
   • Add ‘newNode’ to the list.

Implementation

// C++ program to construct all unique BSTs for keys from 1 to N
#include <bits/stdc++.h>
using namespace std;

// creating Node structure
struct node
{
    int val;
    struct node *left, *right;
};

// Function to create a new BST node
struct node *newNode(int item)
{
    struct node *temp = new node;
    temp->val = item;
    temp->left = temp->right = NULL;
    return temp;
}

// Postorder traversal function
void Postorder(struct node *root)
{
    if (root != NULL)
    {
        Postorder(root->left);
        Postorder(root->right);
        cout << root->val << " ";
    }
}

// Tree construction
vector<struct node *> createTree(int start, int end)
{
    vector<struct node *> list;

    // if start > end,subtree is empty and hence will insert null in the list
    if (start > end)
    {
        list.push_back(NULL);
        return list;
    }

    // iterating over all the values from start to end to construct left and right subtree
    for (int i = start; i <= end; i++)
    {
        // constructing left subtree
        vector<struct node *> lStree = createTree(start, i - 1);

        // constructing right subtree
        vector<struct node *> rStree = createTree(i + 1, end);

        // traversing through all left and right subtrees and connecting them to ith root
        for (int j = 0; j < lStree.size(); j++)
        {
            struct node *left = lStree[j];
            for (int k = 0; k < rStree.size(); k++)
            {
                struct node *right = rStree[k];
                struct node *node = newNode(i); // make value i as root
                node->left = left;              // connecting left subtree
                node->right = right;            // connecting right subtree
                list.push_back(node);           // adding the tree to list
            }
        }
    }
    return list;
}

int main()
{
    // Constructing all possible BSTs
    int n;
    cout << "Enter N: ";
    cin >> n;
    vector<struct node *> treesFrom1toN = createTree(1, n);


    // Print Postorder traversal of all constructed BSTs
    cout << "Postorder traversals of all constructed BSTs:\n";
    for (int i = 0; i < treesFrom1toN.size(); i++)
    {
        Postorder(treesFrom1toN[i]);
        cout << endl;
    }
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

Enter N: 4
Postorder traversals of all constructed BSTs are
4 3 2 1
3 4 2 1
2 4 3 1
3 2 4 1
2 3 4 1
1 4 3 2
1 3 4 2
2 1 4 3
1 2 4 3
3 2 1 4
2 3 1 4
1 3 2 4
2 1 3 4
1 2 3 4

Complexity analysis

Time Complexity: It has exponential time complexity. This is because we use the nth Catalan number to find unique BSTs. As the value of the nth Catalan number is exponential, hence it makes the time complexity exponential.

Space Complexity: O(S*N), where S= Catalan number and N= number of nodes. As there are S unique BSTs, and each BST has N nodes.

You can also read about insertion into bst.

Frequently Asked Questions

How many BSTs can be formed using 3 nodes?

For N=3, there is a total of 5 unique BSTs possible.

How many BSTs can be formed with N keys?

The number of unique binary search trees with N keys equals the Catalan numbers, and the value of Catalan numbers for N=0,1,2,3…., are 1,1,2,5 14,42,132,429,1430, and so on.

Give recurrence relation of the Catalan number.

Recurrence relation of Catalan number:

Conclusion

In this article, we have learned a very important hard-level question on BSTs. We found all the possible BSTs with the key from 1 to the given value(say N).

We hope this blog has helped you enhance your knowledge of Binary Search Trees, to learn more about BSTs, refer to our articles from Binary Search Tree | Learn & Practice from Coding Ninjas Studio. Practice more DSA problems from our Problems List of various companies.

 Check out this problem - Connect Nodes At Same Level

You may also refer to our guided paths on the Coding Ninjas Studio platform to learn more about DSA, DBMS, Competitive Programming, Python, Java, JavaScript, etc. 

Refer to the links problems, top 100 SQL problems, resources, and mock tests to enhance your knowledge. For placement preparations, visit interview experiences and interview bundle.

Do upvote our blog to help other ninjas grow.

Happy Coding!