Description
Construct an N×N ancestor matrix using a binary tree with nodes labelled from 0 to N-1. An ancestor matrix is a boolean matrix in which the cell (i, j) is true if i is a binary tree ancestor of j in a given binary tree. For more intuition of the question, kindly take reference from the below example as shown.
Example:
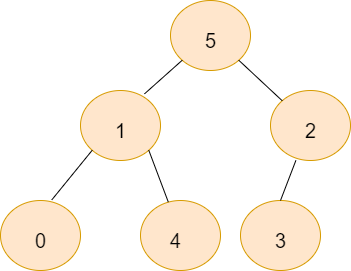
Output:
0 0 0 0 0 0
1 0 0 0 1 0
0 0 0 1 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1 1 1 1 1 0Let's Discuss the method to approach this problem from an interview perspective.
Algorithm Explanation
The intention is to traverse through the tree and Keep track of the ancestors in an array when traversing the tree. When we visit a node, we add it to the ancestor array and consider the row in the adjacency matrix that corresponds to it. All ancestors in that row are given the number one(1). We delete a node from the ancestor array once it has been processed with all of its children.
Let’s look at the implementation of the above approach.
C++ Binary Tree Node Representation
struct TreeNode
{
int data;
TreeNode *left, *right;
};The main Function
C++ Implementation
#include <bits/stdc++.h>
using namespace std;
#define VAR 100
// Global boolean matrix for ease
// To ensure all variables are working smoothly and make dry run easy, all variables are explained below.
// ancestors[] stores all ancestors of current node.
// function fills ancestors for all nodes.
// It also returns size of tree. Size of tree is
// used to print ancestor matrix.
bool matrix[VAR][VAR];
int ancestor_Matrix_from_BT_helper(TreeNode *root, vector<int> &anc)
{
/* base case for this rec func */
if (root == NULL)
return 0;
;
// Update all the ancestors of current node
int data = root->data;
for (int i = 0; i < anc.size(); i++)
matrix[anc[i]][data] = true;
// Push data to the list of ancestors
anc.push_back(data);
// Traverse left and right of the subtrees
int l = ancestor_Matrix_from_BT_helper(root->left, anc);
int r = ancestor_Matrix_from_BT_helper(root->right, anc);
// Remove data from the list of ancestors
// as all descendants of it are processed now.
anc.pop_back();
return l + r + 1;
}
// This helper function to call ancestor_Matrix_from_BT_helper()
void ancestor_Matrix_from_BT(TreeNode *root)
{
// Creating a empty ancestor array
vector<int> ancestors;
// Fill the ancestor matrix and find size of
// tree.
int n = ancestor_Matrix_from_BT_helper(root, ancestors);
// Print the filled values
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
cout << matrix[i][j] << " ";
cout << endl;
}
}
/* Helper function will create a new node */
TreeNode *newnode(int data)
{
TreeNode *node = new TreeNode;
node->data = data;
node->left = node->right = NULL;
return (node);
}
/* Driver program*/
int main()
{
/* Construct the following binary tree
4
/ \
3 1
/ \ \
2 0 5
*/
TreeNode *root = newnode(4);
root->left = newnode(3);
root->right = newnode(1);
root->left->left = newnode(2);
root->left->right = newnode(0);
root->right->left = newnode(5);
ancestor_Matrix_from_BT(root);
return 0;
}
Output:
0 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 0 0
1 0 1 0 0 0
1 1 1 1 0 1
0 0 0 0 0 0Python Binary TreeNode Representation
class newnode:
def __init__(self, data):
self.data = data
self.left = self.right = NonePython Implementation
def length_of(root):
# base case
if root is None:
return 0
return length_of(root.left) + 1 + length_of(root.right)
# Traverse the given tree in a preorder fashion and keep updating the ancestors of
of# all nodes in the ancestor matrix which we declared
def constructAncestorMatrix(root, ancestors, ancestorMatrix):
# base case for the recursive function
if root is None:
return
# updating all the ancestors of the current node
for node in ancestors:
ancestorMatrix[node.data][root.data] = 1
# adding the current node on to the set of ancestors
ancestors.add(root)
# recursion for the left and right subtree of the provided tree
constructAncestorMatrix(root.left, ancestors, ancestorMatrix)
constructAncestorMatrix(root.right, ancestors, ancestorMatrix)
# removing the current node from all the set of ancestors since all
the descendants of the current node are already processed
ancestors.remove(root)
# Function to construct the ancestor matrix from provided binary tree
def Helper(root):
# calculate the length_of of the binary tree
n = length_of(root)
# creating an ancestor matrix of length N*N , initialized at zero
ancestorMatrix = [[0 for x in range(n)] for y in range(n)]
# storing all the ancestors of a node
ancestors = set()
# Construction the ancestor matrix
constructAncestorMatrix(root, ancestors, ancestorMatrix)
return ancestorMatrix
if __name__ == '__main__':
''' Construct the following tree
4
/ \
3 1
/ \ \
2 0 5
'''
root = Node(4)
root.left = Node(3)
root.right = Node(1)
root.left.left = Node(2)
root.left.right = Node(0)
root.right.right = Node(5)
ancestorMatrix = Helper(root)
#To show the Matrix
for row in ancestorMatrix:
print(row)
Output:
0 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 0 0
1 0 1 0 0 0
1 1 1 1 0 1
0 0 0 0 0 0Time Complexity and Space Complexity
Time complexity: O(N)
O(N) for accessing left and right node in helper function and another O(N) for utility function to call a helper function
Space Complexity O(N2)
O(N2) for storing the ancestors in a 2D matrix, where N is the size of the binary tree.
Check out this problem - Diameter Of Binary Tree





