Convert a Sorted Linked List to Balanced BST

Naive/Recursive Approach

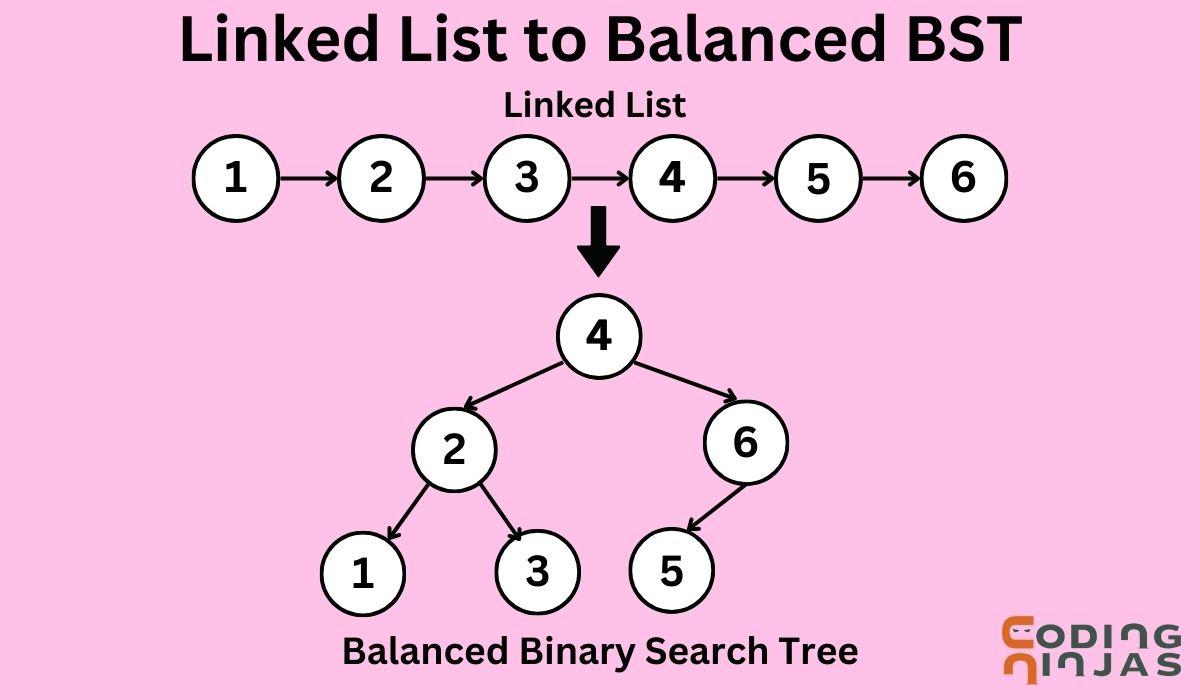
Suppose we are given a sorted linked list:

Since the linked list is sorted in increasing order, we can divide it into two halves from the middle element. One half contains the smaller values, and the other half contains the larger values. This is the basic idea behind our approach. The middle element forms the root, the left half forms the left subtree, and the right half forms the right subtree. Then, recursively call for the construction of the left and right subtree. 

Now, you're probably wondering why we chose the middle element of the array as the root of our balanced BST.

When we are creating a balanced BST, we want nodes with smaller values on the left side of the root node and nodes with larger values on the right side of the root node. The second requirement is that the tree must be balanced. So, we'll aim to have equal nodes on both sides of the central element. With these conditions in mind, we quickly answer that the middle element of the array will be the perfect choice for the root node since it's a sorted array, all values on the left side will be smaller than the middle value. We'll find greater values on the right side of the middle element.

It is recommended to try the stated problem on your own before jumping to the solution.

Algorithm

1. Find the position of the middle element of the linked list. If there are two middle elements, we can consider either of them. In this article, we have considered the second one.

2. Create a node with this element as its value.

3. Make two recursive calls, one for the left subtree with the left half of the current linked list, that is, the elements before the element selected as root, and the other call for the right half elements.

4. Repeat steps 1,2, and 3 until no element is left in the linked list to be formed as a node.

Dry Run

For input of sorted linked list = { 1, 2, 3, 4, 5, 6 }, middle element= 4

Construct a root node with 4 as the value and call for its left and right subtree with the left and right half of the Linked list, respectively.

Next, select the middle element of the left half, that is, {2}. Construct a node with {2} as the value. The elements to the left of {2} form its left subtree, while the elements to the right of {2} form its right subtree. Since we have only one element on either side, {1} forms its left subtree, while {3} forms its right subtree.

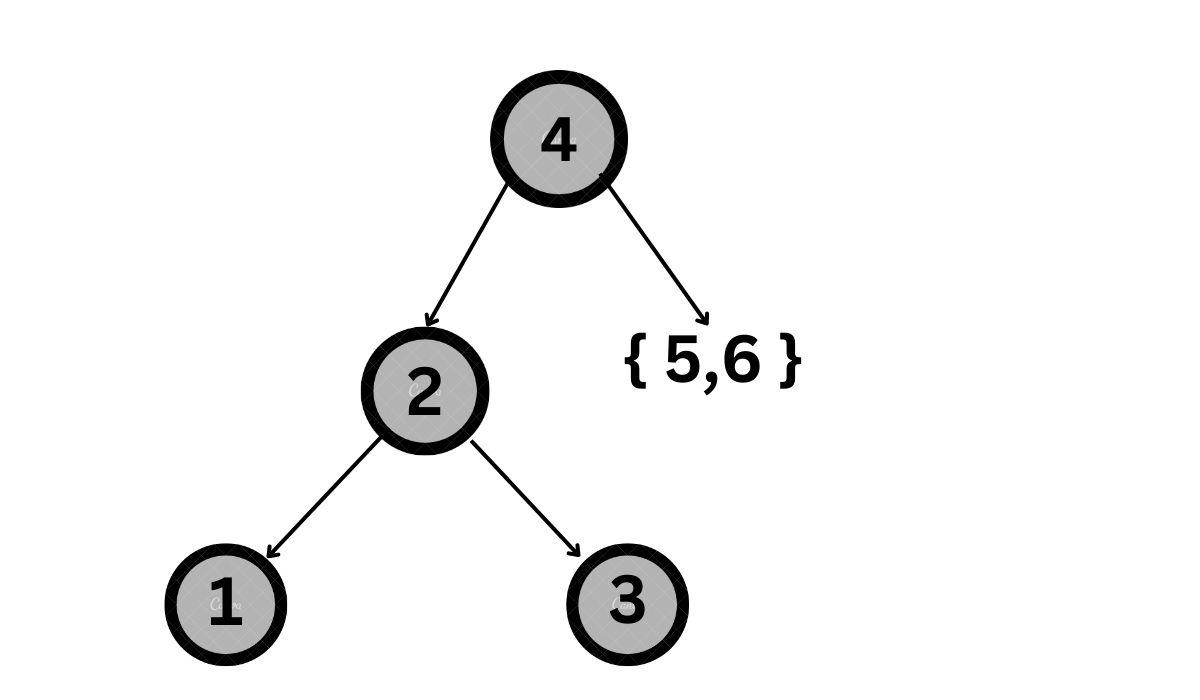
Next, for the right half, select the middle element. Since there are two middle elements, we can select either of them. Let us consider 6. Construct a node with 6 as the value and 5 as its left subtree, as 5 is towards the left half of 6.

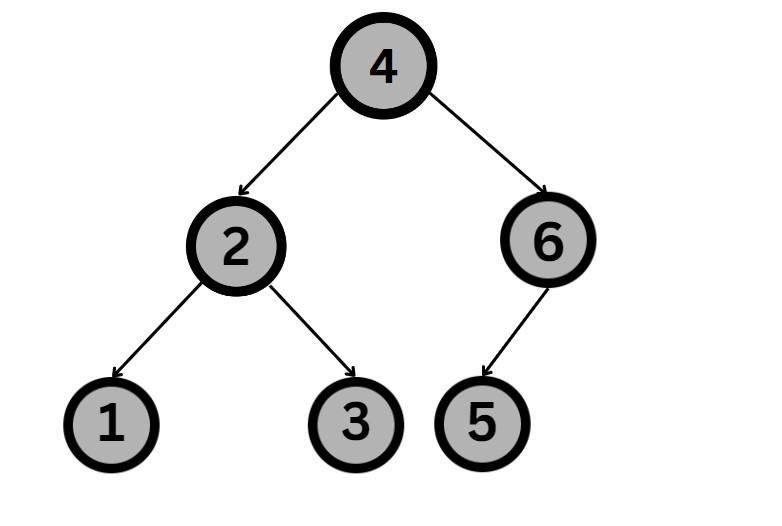
As we can see, the above tree is a binary search tree since all the values in the left subtree are lesser than the root node, all the values in the right subtree are greater than the root, and the left and right subtrees are also BSTs.

Also, we can observe that the above tree is a balanced binary tree. The preorder traversal of the above tree, and hence the output will be 4 2 1 3 6 5.

Implementation in C++

Let’s have a look at the code for converting a sorted linked list to a balanced BST in C++.

#include <iostream>
using namespace std;

// Class representing the nodes of the linked list
class ListNode{
public:
    int value;
    ListNode *next;
    ListNode(int a){
        // Constructor to initialize the value of the linked list node.
        value = a;
    }
};

// Class representing the nodes of the binary tree
class TreeNode{
public:
    int value;
    TreeNode *left;
    TreeNode *right;
    // Constructor to initialize the value of the tree node
    TreeNode(int a){
        value = a;
    }
};

// Function for pre-order traversal of the obtained tree
void preorder(TreeNode *root){
    if (root != NULL){
        cout << root->value << " ";
        preorder(root->left);
        preorder(root->right);
    }
}

// Function to convert the given linked list into a balanced binary search tree.
TreeNode *sortedListToBalancedBST(ListNode *node){

    // If the node is null, return it
    if (node == NULL){
        return NULL;
    }
    
    // Counting the number of nodes present in the linked list
    ListNode *temp = node;
    int n = 0;
    while (temp != NULL){
        n++;
        temp = temp->next;
    }
    
    /*
    	If there is only one node in the linked list, 
    	construct a root node with its value and return it.
    */
    if (n == 1){
        return new TreeNode(node->value);
    }
    
    // First n/2 nodes contribute to the left subtree
    ListNode *lefttree = new ListNode(node->value);
    ListNode *leftTemp = lefttree;
    
    for (int i = 0; i < n / 2 - 1; i++){
        node = node->next;
        leftTemp->next = new ListNode(node->value);
        leftTemp = leftTemp->next;
    }
    
    node = node->next;
    
    /*
    	Node points to the middle element of the linked list
    	So, we will make this element as the root of the BST
    */
    TreeNode *root = new TreeNode(node->value);
    
    // Move node ahead
    node = node->next;
    
    // Remaining nodes are considered for the right subtree
    ListNode *righttree = NULL;
    
    if (node != NULL){
        righttree = new ListNode(node->value);
        ListNode *rightTemp = righttree;
        node = node->next;
        while (node != NULL){
            rightTemp->next = new ListNode(node->value);
            rightTemp = rightTemp->next;
            node = node->next;
        }
    }
    
    // Recursively call the method for left and right halfs
    root->left = sortedListToBalancedBST(lefttree);
    root->right = sortedListToBalancedBST(righttree);
    return root;
}

int main(){
    // Create the linked list
    ListNode *node = new ListNode(1);
    node->next = new ListNode(2);
    node->next->next = new ListNode(3);
    node->next->next->next = new ListNode(4);
    node->next->next->next->next = new ListNode(5);
    node->next->next->next->next->next = new ListNode(6);
    
    TreeNode *root = sortedListToBalancedBST(node);
    
    // Printing the linked list elements
    cout << "The elements of linked list are: ";
    ListNode *temp = node;
    while (temp != NULL){
        cout << temp->value << " ";
        temp = temp->next;
    }
    cout << endl;
    
    cout << "The preorder traversal of the obtained tree is: ";
    preorder(root);
    cout << endl;
    return 0;
}

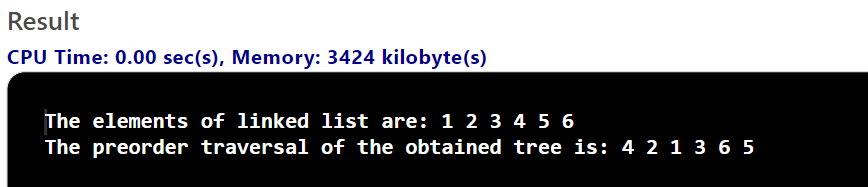
Output

Implementation in Java

import java.util.*;

// Class representing the nodes of the linked list
class ListNode {
    int value;
    ListNode next;
    ListNode(int a) {
        value = a;
    }
}

// Class representing the nodes of the BST
class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    TreeNode(int a) {
        value = a;
    }
}

class Main {
    // Function for pre-order traversal of a tree
    static void preorder(TreeNode root) {
        if (root != null) {
            System.out.print(root.value + " ");
            preorder(root.left);
            preorder(root.right);
        }
    }

    // Function to convert the linked list to balanced binary search tree.
    static TreeNode sortedlistToBalancedBST(ListNode node) {
        // If the node is null, return it
        if (node == null) {
            return null;
        }
        
        // Counting number of nodes present in the linked list
        ListNode temp = node;
        int n = 0;
        while (temp != null) {
            n++;
            temp = temp.next;
        }
        
        /*
            If there is only one node in the linked list, 
            create a root node using it and return it.
        */
        if (n == 1) {
            return new TreeNode(node.value);
        }
        
        // First n/2 nodes contribute to the left subtree
        ListNode lefttree = new ListNode(node.value);
        ListNode leftTemp = lefttree;
        for (int i = 0; i < n/2 - 1; i++) {
            node = node.next;
            leftTemp.next = new ListNode(node.value);
            leftTemp = leftTemp.next;
        }
        
        node = node.next;
        
        /*
            Node points to the middle element of the linked list
            So, we will make this element as the root of the BST
        */
        TreeNode root = new TreeNode(node.value);
        
        // Move node ahead
        node = node.next;
        
        // Remaining nodes are considered for the right subtree
        ListNode righttree = null;
        if (node != null) {
            righttree = new ListNode(node.value);
            ListNode rightTemp = righttree;
            node = node.next;
            while (node != null) {
                rightTemp.next = new ListNode(node.value);
                rightTemp = rightTemp.next;
                node = node.next;
            }
        }
        
        // Recursively call the method for left and right halfs
        root.left = sortedlistToBalancedBST(lefttree);
        root.right = sortedlistToBalancedBST(righttree);
        return root;
    }

    public static void main(String[] args) {
        // Create a linked list
        ListNode node = new ListNode(1);
        node.next = new ListNode(2);
        node.next.next = new ListNode(3);
        node.next.next.next = new ListNode(4);
        node.next.next.next.next = new ListNode(5);
        node.next.next.next.next.next = new ListNode(6);
        
        TreeNode root = sortedlistToBalancedBST(node);
        
        // Printing the linked list elements 
        System.out.print("The elements of linked list are: ");
        ListNode temp=node;
        while(temp!=null){
            System.out.print(temp.value+" ");
            temp=temp.next;
        }
        
        System.out.println();
        System.out.print("The preorder traversal of the obtained tree is: ");
        preorder(root);
        System.out.println();
    }
}

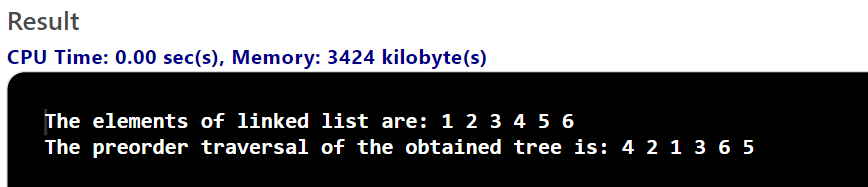
Output

Time Complexity

O(N log N)

The time complexity of this code will be O(NlogN), where ‘N’ is the size of the sorted linked list. 

As it is a balanced binary tree, height will be at most log N. For every level of the BST, we are iterating over the complete linked list to find the middle element; thus, the time complexity will be O(NlogN).

Space Complexity

O(log N)

The space complexity of this code will be (log(N)), where ‘N’ is the size of the given linked list. 

The recursion call stack will store function calls up to the tree’s height, and the tree is balanced; thus, in the worst case, the height will be log(N). Hence the overall space complexity will be O(logN).

Optimal Approach 

The approach discussed above can be optimized if we start building the binary tree from the leaf nodes to the root node of the BST.

The basic idea behind this approach is to build the left subtree, then the root node, and then the right subtree. After doing so, we will attach both subtrees to the root node.

Algorithm

1. Count the number of nodes present in the sorted linked list. Let the count of nodes be n.
    
2. After getting the count, we will take the first n/2 nodes and construct the left subtree.
    
3. The very next node after the n/2 node makes the root node of the BST. Further, we link the left subtree with the root node.
    
4. Then, with the remaining nodes, we construct the right subtree. After linking it with the root node, our balanced BST is formed.

Dry Run

Let us consider the input linked list as { 1, 2, 3, 4, 5, 6 }. 

1. As explained above, first n/2 nodes make up the left subtree, the next node makes the root of the tree, and the remaining nodes make up the right subtree.

For the first time, the count of nodes=6.

2. A recursive call will be made for the first half nodes to construct the left subtree.

Therefore, the second time, the count of nodes=3.

3. Similarly, next time, a call will be made with n=1.

Now, a tree node will be constructed since we have only one linked list node under consideration. 

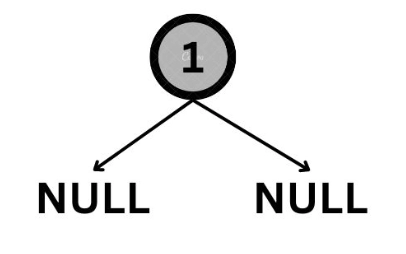
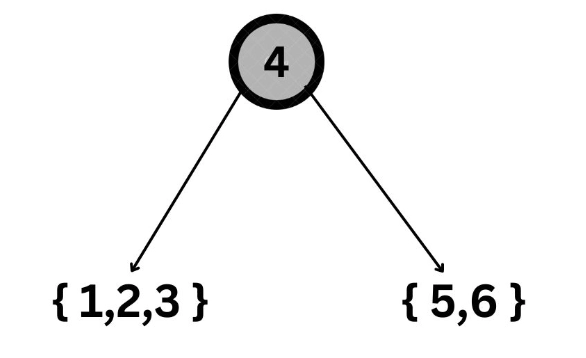
4. Next, a treenode will be constructed with the next value in the preorder traversal, which is {2}. And the above-constructed tree will be attached as its left subtree. 

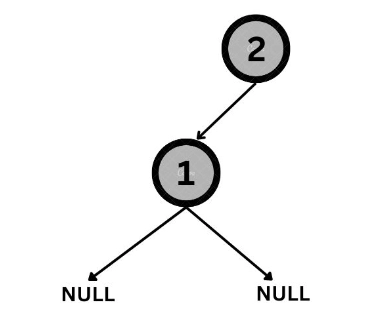
5. Next, a recursive call will be made with (n-n/2-1) next elements to construct the right subtree. At this stage, n=3. Therefore, n-n/2-1=1.
The next node, which is {3}, will be used to construct the right subtree of the current root, which is {2}.

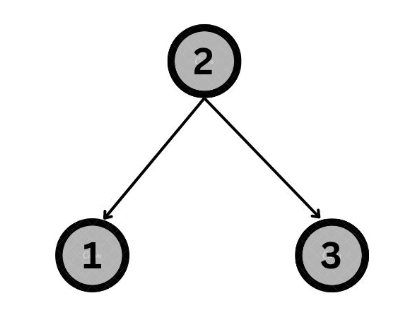
6. The above-obtained tree will be the left subtree of the tree node constructed using the next value in the preorder traversal, which is { 4 }.

At this stage, n=6. The next (n-n/2-1) nodes will be used to construct the right subtree of the current root. n-n/2-1= 2. Thus, the next two nodes of the preorder traversal { 5,6 } will form the right subtree in a similar manner.

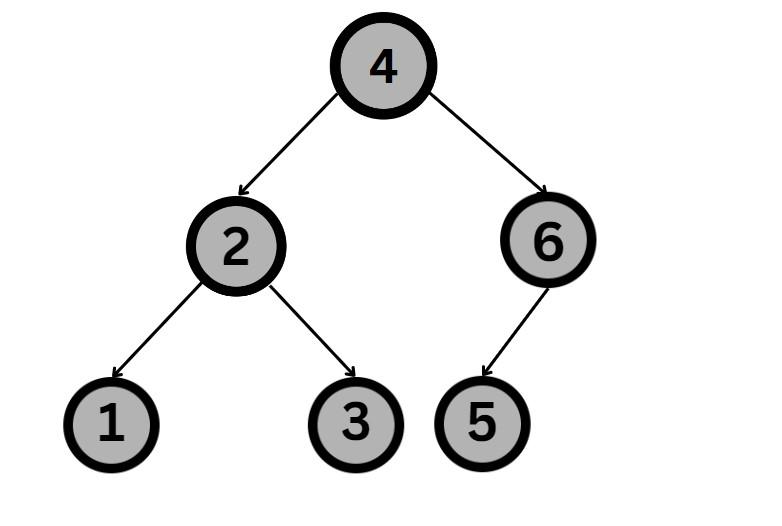
Hence we obtained a balanced binary search tree from the given linked list in O(N) time complexity. The preorder traversal of the above-obtained tree is as 4 2 1 3 6 5.

Let us now see how we can implement this efficient approach.

Implementation in C++

Let’s have a look at the code for converting a sorted linked list to balanced BST:

#include <iostream>
using namespace std;

// Class representing the nodes of a linked list
class ListNode{
public:
    int value;
    ListNode *next;
    // Constructor
    ListNode(int a){
        value = a;
    }
};

// Class representing the nodes of the BST
class TreeNode{
public:
    int value;
    TreeNode *left;
    TreeNode *right;
    // Constructor
    TreeNode(int a){
        value = a;
    }
};

ListNode *globalNode = NULL;
// Function for pre-order traversal of a tree
void preorder(TreeNode *root){
    if (root != NULL){
        cout << root->value << " ";
        preorder(root->left);
        preorder(root->right);
    }
}

TreeNode *sortedlistToBalancedBSTRecursive(int n){
    /*
    	If the count of nodes is less than or equal 
    	to zero, then return a NULL node
    */
    if (n <= 0){
        return NULL;
    }
    
    // First n/2 nodes will be required to construct the left subtree.
    TreeNode *leftSubTree = sortedlistToBalancedBSTRecursive(n / 2);
    
    // Constructing the root node
    TreeNode *root = new TreeNode(globalNode->value);
    globalNode = globalNode->next;
    
    // Linking the left subtree with the root node
    root->left = leftSubTree;
    
    /*
    	Constructing right subtree and linking it with the root node 
    	The right subtree has (n - n/2 - 1) nodes
    */
    root->right = sortedlistToBalancedBSTRecursive(n - n / 2 - 1);
    return root;
}

TreeNode *sortedlistToBalancedBST(ListNode *head){
    // Counting number of nodes present in the linked list
    int n = 0;
    ListNode *temp = head;
    while (temp != NULL){
        n++;
        temp = temp->next;
    }
    globalNode = head;
    return sortedlistToBalancedBSTRecursive(n);
}

int main(){
    // Construct the linked list
    ListNode *node = new ListNode(1);
    node->next = new ListNode(2);
    node->next->next = new ListNode(3);
    node->next->next->next = new ListNode(4);
    node->next->next->next->next = new ListNode(5);
    node->next->next->next->next->next = new ListNode(6);
    
    TreeNode *root = sortedlistToBalancedBST(node);
    
    // Printing the linked list elements 
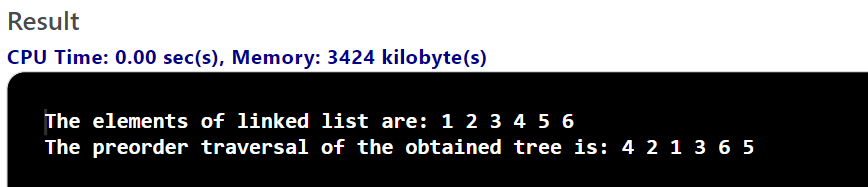
    cout<<"The elements of linked list are: ";
    ListNode *temp=node;
    while(temp!=NULL){
        cout<<temp->value<<" ";
        temp=temp->next;
    }
    
    cout<<endl;
    cout<<"The preorder traversal of the obtained tree is: ";
    preorder(root);
    cout << endl;
    return 0;
}

Output

Implementation in Java

import java.util.*;

// Class representing the nodes of a linked list
class ListNode {
    public int value;
    public ListNode next;
    public ListNode(int a) {
        value = a;
    }
}

// Class representing the nodes of the BST
class TreeNode {
    public int value;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int a) {
        value = a;
    }
}

public class Main {
    static ListNode globalNode = null;
    // Function for pre-order traversal of a tree
    public static void preorder(TreeNode root) {
        if (root != null) {
            System.out.print(root.value + " ");
            preorder(root.left);
            preorder(root.right);
        }
    }
    
    public static TreeNode sortedlistToBalancedBSTRecursive(int n) {
        /*
            If the count of nodes is less than or equal 
            to zero, then return a NULL node
        */
        if (n <= 0) {
            return null;
        }
        
        // First n/2 nodes will be required to construct the left subtree.
        TreeNode leftSubTree = sortedlistToBalancedBSTRecursive(n/2);
        
        // Constructing the root node
        TreeNode root = new TreeNode(globalNode.value);
        globalNode = globalNode.next;
        
        // Linking the left subtree with the root node
        root.left = leftSubTree;
        
        /*
            Constructing the right subtree and linking it with 
            the root node. The right subtree has (n - n/2 - 1) nodes
        */
        root.right = sortedlistToBalancedBSTRecursive(n - n/2 - 1);
        return root;
    }
    
    public static TreeNode sortedlistToBalancedBST(ListNode node) {
        // Counting number of nodes present in the linked list
        int n = 0;
        ListNode temp = node;
        while (temp != null) {
            n++;
            temp = temp.next;
        }
        
        globalNode = node;
        return sortedlistToBalancedBSTRecursive(n);
    }
    
    public static void main(String[] args) {
        // Creating the linked list
        ListNode node = new ListNode(1);
        node.next = new ListNode(2);
        node.next.next = new ListNode(3);
        node.next.next.next = new ListNode(4);
        node.next.next.next.next = new ListNode(5);
        node.next.next.next.next.next = new ListNode(6);
        
        TreeNode root = sortedlistToBalancedBST(node);
        
        // Printing the linked list elements
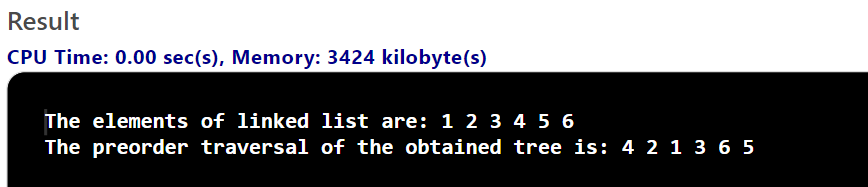
        System.out.print("The elements of linked list are: ");
        ListNode temp=node;
        while(temp!=null){
        System.out.print(temp.value+" ");
        temp=temp.next;
        }
    
        System.out.println();
        System.out.print("The elements of preorder traversal are ");
        preorder(root);
        System.out.println();
    }
}

Output

Time Complexity

O(N)

The time complexity of the above code will be O(N), where ‘N’ is the number of nodes of the BST.

The time required to find the size of the linked list will be O(N). Then, during the construction of the balanced BST, we will visit each node exactly once. So overall time complexity is O(N).

Space Complexity

O(log N)

The space complexity of this code will be O(log(N)), where ‘N’ refers to the size of the given linked list. 

The recursion call stack will store function calls up to the tree’s height, and the tree is balanced; thus, the height will be log(N). Hence the overall space complexity will be O(logN).

Frequently Asked Questions

What is a linked list?

A linked list is a linear data structure in which the data elements are not stored at one place in the memory but instead at different places.

What are the types of linked list?

Linked lists are of three types- singly linked list, doubly linked list and circular linked list. 

What is a Binary Tree?

 A binary tree is a tree data structure where each node has at most 2 children. 

What is a Balanced Binary Tree? 

A balanced binary tree is a binary tree where the height of left and right subtree differs at maximum by one for all the nodes. 

How do you know if BST is balanced?

A BST is balanced when the height difference between the left and right subtrees is either zero or one for all the tree nodes.

Conclusion

In this blog, we discussed the approach for converting a sorted linked list to a balanced BST (Binary Search Tree). In a balanced BST, the difference between the height of the left subtree and the right subtree should not be greater than one. We discussed two approaches starting with the basic one and moving on to the most optimal solution in the C++ and Java Programming Language.

You can visit more relatable articles on Coding Ninjas Studio-

1. Check if Binary Tree Contains a Balanced BST of Size K
2. Check if Binary Tree Is BST or Not
3. Check if a given binary tree is a subtree of another binary tree or not
4. Doubly Linked List
    

Try practicing this question here on your own. Do share this blog with your friends. 

And many more on our platform Coding Ninjas Studio.Refer to our Guided Path to upskill yourself in DSA, Competitive Programming, JavaScript, System Design, and many more! If you want to test your competency in coding, you may check out the mock test series and participate in the contests hosted on Coding Ninjas Studio!

If you have just started your learning process and are looking for questions from tech giants like Amazon, Microsoft, Uber, etc. In that case, you must look at the problems, interview experiences, and interview bundles for placement preparations.

However, you may consider our paid courses to give your career an edge over others!

Happy Learning, Ninjas!