Convert the Given binary Tree into a Symmetric Tree by adding a minimum number of nodes

Introduction

Binary trees are like salt to an interview,i.e., every tech interview is incomplete without binary trees. Thus to get an edge over our competition, it is very important to master binary trees. But when Ninja is here, you don’t have to go to any other place. Today we will be seeing one such important problem on Binary Trees, 

Also see, Data Structures

Problem Statement

The problem states that we need to convert the given binary tree into a symmetric Tree by adding a minimum number of nodes. If two nodes have different values opposite each other, then replace the value of both nodes with their sum. 

Let us recap what a binary tree is, and a symmetric tree is: 

Binary Tree:

As the name suggests, a binary tree is a tree in which every node can have at most two children, and they are known as the left and right children. 

Symmetric Tree:

The symmetric tree is a special type of tree, which is a mirror image of itself about the root node. When we divide the tree along with the root node, the two trees we will get will be identical. 

Sample Examples

Example 1:

Input: Given The binary Tree, convert it into a symmetric Tree. 

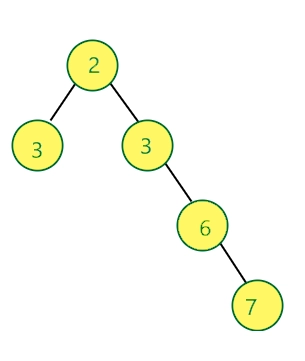
Output: 

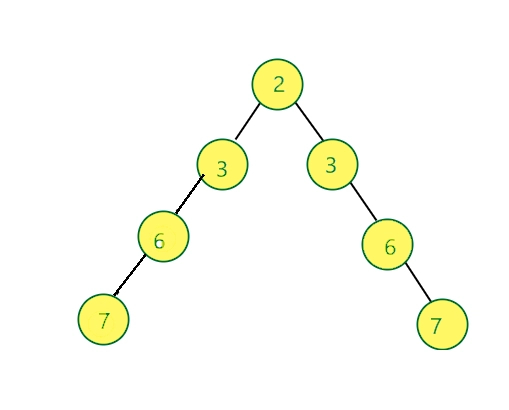
Explanation: We have added two nodes, i.e., a node with value 3 and value 4  in the left subtree of the root node, to make the given binary tree into a symmetric tree.

Example 2:

Input: Given The binary Tree, convert it into a symmetric Tree.

Output: 

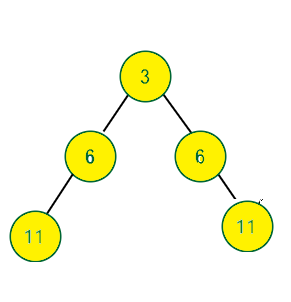
Explanation: 

In the right subtree, we replace the node with the value 4 with 4 + 2(because the node with value 2 is at symmteric position with this node), which becomes 6. 

We replace the node with value 6 in the right subtree with value 5 + 6(because the node with value 5 is at symmetric position with this node), which becomes 11. . 

Solution Approach

The idea is simple, we travel the right and left subtree of the root and the nodes at symmetrical places to one another; we will check, and if any node does not exist, we will create and insert that node. If the value of nodes with symmetric places is not the same, we will replace the values of both nodes with the sum of both nodes. 

Steps of Algorithm

1. Make a function convertSymmetric(), and it will accept two parameters, namely root1, and root2, root1, and root2 are the nodes at symmetrical places with respect to one another. 
2. There can be 2 cases possible, either root1 or root2 does not exist, or the values of root1 and root2 are not the same. 
3. If root2 exists and root1 does not exist, create a new node with a value the same as root2 and insert it at the position of root1 and vice-versa if root 1 exists and root2 does not exist.
4. Now make recursive call for symmetric position to a function convertSymmetric(root1->left, root2->right) and convertSymmetric(root1->right, root->left). 
5. The Binary tree will become a symmetric tree after all recursive calls is over.  

Implementation in C++

// C++ implementation of the above approach
#include<bits/stdc++.h>
using namespace std;
// declaring the structure of the
// Tree Node
class TreeNode{
    public:
        TreeNode *left, *right;
        int data;
    TreeNode(int data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};

// utility function to convert the given
// tree into the symmetric tree
TreeNode* convertSymmetric(TreeNode *root1, TreeNode *root2){
    // Base Case,
    // If both root1 and root2 are NULL
    if(!root1 && !root2){
        return NULL;
    }
    // if  root2 exist, but root1 is NULL
    if(!root1){
        TreeNode* newNode = new TreeNode(root2->data);
        root1 = newNode;
    }
    // if root1 exist, but root2 is NULL
    if(!root2){
        TreeNode *newNode = new TreeNode(root1->data);
        root2 = newNode;
    }
    // if both roo1 and root2 exist, but
    // their values are not same,
    // replace both the nodes
    // with their sum
    if(root2->data != root1->data){
        int sum = root1->data + root2->data;
        root1->data = sum;
        root2->data = sum;
    }
    // call the recursive function
    // call to the left
    root1->left = convertSymmetric(root1->left, root2->right);
    // calling to the right
    root1->right = convertSymmetric(root1->right, root2->left);
    return  root1;
}

void inorder(TreeNode *root){
    if(!root)
        return;
    inorder(root->left);
    cout << root->data << " ";
    inorder(root->right);
}

int main(){
    // inserting the nodes into the tree
    TreeNode *root = new TreeNode(3);
    root->left = new TreeNode(2);
    root->left->left = new TreeNode(5);
    root->right = new TreeNode(4);
    root->right->right = new TreeNode(6);
    cout << "Inorder Traversal before  calling the function: ";
    inorder(root);
    root = convertSymmetric(root, root);
    cout << endl << "Inorder Traversal After calling the function: ";
    inorder(root);
}

You can also try this code with Online C++ Compiler

Run Code

Output: 

Inorder Traversal before calling the function: 5 2 3 4 6
Inorder Traversal After calling the function: 11 6 3 6 11

Complexity Analysis

Time Complexity: O(N)

Explanation: Since we are traversing the complete binary tree only once, hence its time complexity is O(N). 

Space Complexity: O(1)

Explanation: No extra space is used. 

Check out this problem - Mirror A Binary Tree