Introduction
In this article, we will discuss the problem to count divisible pairs in an array and briefly discuss the approach to be used and its time and space complexity. Before discussing count divisible pairs in an array problem, let’s first discuss what an array means.
Array: It is a linear data structure consisting of a collection of values called elements of an array, stored in a contiguous memory location, and can be accessed using array indexes.

In this problem, we are given an array of any size(provided by the user), and our task is to count division pairs in an array. You may be wondering🤔 what this division pair is. Here is the answer 😃👉
Division pair: If one element of a pair divides another element, then such a pair is called a division pair.
Example:

Recommended topic, kth largest element in an array and Euclid GCD Algorithm
Native Approach
Using brute force, iterating through each element of an array and checking if pair (‘i’,’j’) are such that ‘a[i]’ % ‘a[j]’ = 0 or not.
Algorithm
- Take array size as input ‘n’.
- Create an array of size ‘n’, lets say, ‘a[n]’.
- Take a temporary variable ‘count’ for counting division pairs.
- Start a for loop from ‘i’ = 0 to ‘n-1’.
- Inside this loop, start another for loop from ‘j’ = ‘i+1’ to ‘n-1’.
- Inside these loop check if ‘a[i]’ % ‘a[j]’ = 0 or ‘a[j]’ % ‘a[i]’ = 0.
- If the condition is true, increment the ‘count’ variable.
- Else continue.
- Return ‘count’.
- Print the result.
Code in C++ 💻
/*
Program to count divisible pairs in an array.
*/
#include <iostream>
using namespace std;
int countPairs(int a[], int n)
{
int count = 0;
// Iterate through all pairs
for (int i=0; i<n; i++)
{
for (int j=i+1; j<n; j++)
{
// Increment count if one divides other
if (a[i] % a[j] == 0 || a[j] % a[i] == 0)
count++;
}
}
return count;
}
int main()
{
int n;
cout<<"Enter array size : ";
cin>>n;
int a[n];
cout<<"\nEnter array elements : ";
for(int i=0;i<n;i++)
cin>>a[i];
cout << countPairs(a, n);
return 0;
}Code in Java 💻
/*
Java program to count divisible pairs in an array.
*/
import java.util.Scanner;
class CodingNinjas {
static int countPair(int arr[],int n)
{
int count = 0;
// Iterate through all pairs
for (int i=0; i<n; i++)
{
for (int j=i+1; j<n; j++)
{
// Increment count if one divides other
if (a[i] % a[j] == 0 || a[j] % a[i] == 0)
count++;
}
}
return count;
}
// Driver Code
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
System.out.print("Enter array size : ");
n=sc.nextInt();
int a[] = new int[n]
System.out.println("Enter array elements : ");
for(int i=0; i<n; i++)
{
a[i] = sc.nextInt();
}
System.out.print(countPairs(a, n));
}
} Code in Python 💻
# Python3 program to count divisible pairs in an array.
def countPair(a, n) :
count = 0
# Iterate through all pairs
for i in range(0, n) :
for j in range(i+1, n) :
# Increment count if one divides other
if (a[i] % a[j] == 0 or a[j] % a[i] == 0) :
count+=1
return count
# Driver code
if __name__=='__main__':
n=int(input("Enter array size : "))
a=list(map(int, input("Enter array elements : ").strip().split()))
print(countPair(a, n))Output
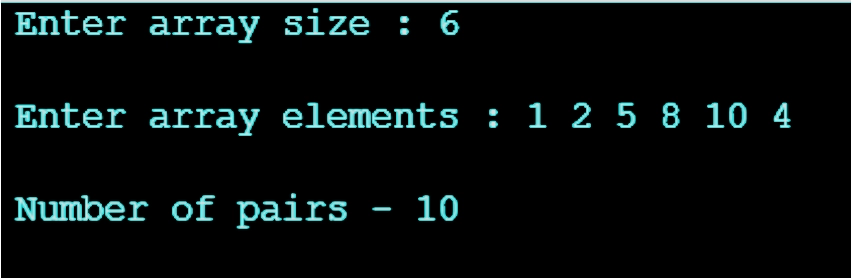

Time and Space Complexity
We have used two loops in the program, one is a single for loop iterating from 0 to ‘N’, This will take O(N) time complexity.
Another loop is a nested loop used to count division pairs in an array, this loop iterates from 0 to ‘N’ and ‘i + 1’ to ‘N’, this will take O(N*N) time complexity.
🎀Total time complexity = O(N) + O(N*N) = O(N*N)
🎀Space Complexity = O(N), for an array of size N.
Although the program is simple, but it is not an efficient solution for this problem, let’s discuss an efficient approach, that is by hashing.😉





