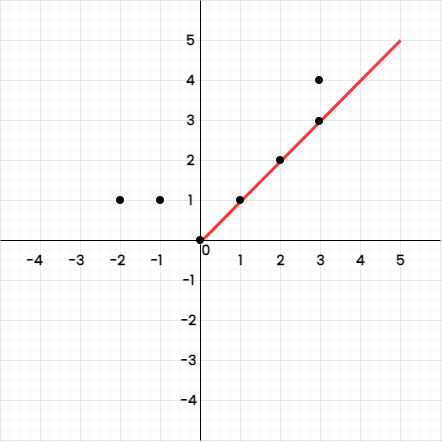
Approach
Our approach to count maximum points on same line will be simple we will simply calculate the slope from one point (i) to all the other points. And save them in a hash table.
Then we move to the next point (i+1) and similarly calculate the slopes of all the respective points.
Algorithm
-
Create a function to find the maximum collinear point.
-
Created an ordered map to store the slopes of the points.
-
Run a nested for loop to calculate the slope between all the points.
-
If both points are equal, then just increase the overlapping(same) count.
-
If the x coordinate is the same, then both points are vertical to each other.
-
Calculate the slope stored in the map.
-
Return the max value of the hash table.
Let's understand the algorithm with the help of an example.
Points[] = {-1, 1}, {0, 0}, {1, 1}, {2, 2}
Step 1: Find the slope from one point to all other points and store it on the map.
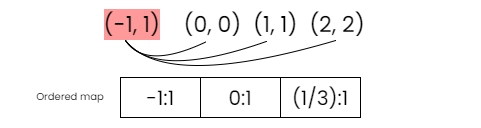
Step 2:Find the slope of the next point to all other points and store it on the map.
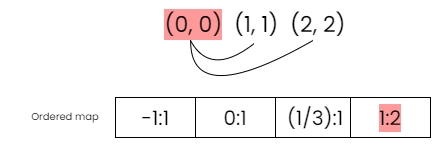
Step 3: Similarly find the slope from one point to all other points and store it on the map.
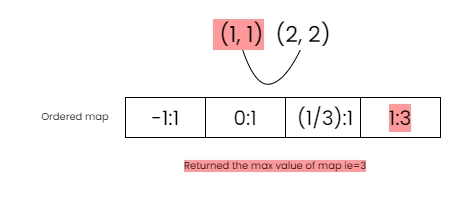
Step 4: Return the max value of hash i.e. =3
Code in C++
Implementation of C++ code to count maximum points on same line.
#include <bits/stdc++.h>
using namespace std;
/* Create a function to find the maximum collinear point */
int maxPoints(vector<vector<int>> &points)
{
int res = 0;
for (int i = 0; i < points.size(); i++)
{
map<long double, int> mp;
int same = 1, l = 0;
for (int j = i + 1; j < points.size(); j++)
{
/* checking for equal points */
if (points[i][0] == points[j][0] && points[i][1] == points[j][1])
{
same++;
}
/* checking for vertical points */
else if (points[i][0] == points[j][0])
{
mp[INT_MAX]++;
}
/* calculating the slopes for all the other points */
double d = ((long double)(points[j][1] - points[i][1])) / ((long double)(points[j][0] - points[i][0]));
mp[d]++;
}
for (auto it : mp)
{
l = max(l, it.second);
}
l += same;
res = max(res, l);
}
return res;
}
int main()
{
const int N = 6;
int arr[N][2] = {{-1, 1}, {0, 0}, {1, 1}, {2, 2}, {3, 3}, {3, 4}};
vector<vector<int>> points;
for (int i = 0; i < N; i++)
{
vector<int> temp;
temp.push_back(arr[i][0]);
temp.push_back(arr[i][1]);
points.push_back(temp);
}
cout << maxPoints(points) << endl;
return 0;
}

You can also try this code with Online C++ Compiler
OUTPUT
4
Code in Python3
Implementation of Python3 code to count maximum points on same line.
from math import gcd
from collections import defaultdict
from typing import DefaultDict, List, Tuple
IntPair = Tuple[int, int]
def slope(a: IntPair, b: IntPair) -> IntPair:
run = b[0] - a[0]
if run == 0:
return (1, 0)
if run < 0:
a, b = b, a
run = b[0] - a[0]
rise = b[1] - a[1]
gcd_ = gcd(abs(rise), run)
return (
rise // gcd_,
run // gcd_,
)
def points_on_same_line(points: List[List[int]]) -> int:
if len(points) < 3:
return len(points)
max_value = 0
for p_index in range(0, len(points) - 1):
a = tuple(points[p_index])
slope_counts: DefaultDict[IntPair, int] = defaultdict(lambda: 1)
for q_index in range(p_index + 1, len(points)):
b = tuple(points[q_index])
slope_counts[slope(a, b)] += 1
max_value = max(
max_value,
max(slope_counts.values()),
)
return max_value
print(points_on_same_line([
[-1, 1],
[0, 0],
[1, 1],
[2, 2],
[3, 3],
[3, 4],
]))

You can also try this code with Online Python Compiler
OUTPUT
4
Code in Java
Implementation of Java code to count maximum points on same line.
import java.util.*;
public class collinearPoint {
/* Create a function to find the maximum collinear point */
public static int maxPoints(ArrayList<ArrayList<Integer>> points) {
int res = 0;
for (int i = 0; i < points.size(); i++) {
HashMap<Double, Integer> mp = new HashMap<>();
int same = 1, l = 0;
for (int j = i + 1; j < points.size(); j++) {
/* checking for equal points */
if (Objects.equals(points.get(i).get(0), points.get(j).get(0))
&& Objects.equals(points.get(i).get(1), points.get(j).get(1))) {
same++;
}
/* checking for vertical points */
else if (Objects.equals(points.get(i).get(0), points.get(j).get(0))) {
int val = mp.getOrDefault((double) Integer.MAX_VALUE, 0) + 1;
mp.put((double) Integer.MAX_VALUE, val);
}
/* calculating the slopes for all the other points */
double d = ((double) (points.get(j).get(1) - points.get(i).get(1)))
/ ((double) (points.get(j).get(0) - points.get(i).get(0)));
int val = mp.getOrDefault(d, 0) + 1;
mp.put(d, val);
}
for (Map.Entry<Double, Integer> m : mp.entrySet()) {
l = Math.max(l, m.getValue());
}
l += same;
res = Math.max(res, l);
}
return res;
}
public static void main(String[] args) {
int N = 6;
int[][] arr = {
{ -1, 1 },
{ 0, 0 },
{ 1, 1 },
{ 2, 2 },
{ 3, 3 },
{ 3, 4 }
};
ArrayList<ArrayList<Integer>> points = new ArrayList<>();
for (int i = 0; i < N; i++) {
ArrayList<Integer> temp = new ArrayList<>();
temp.add(arr[i][0]);
temp.add(arr[i][1]);
points.add(temp);
}
System.out.print(maxPoints(points));
System.out.print("\n");
}
}

You can also try this code with Online Java Compiler
OUTPUT
4
Time Complexity: O(n2logn)
There is nested loops present and we used the map data structure to save the slope points. Hence the time complexity is O(n2logn).
Auxiliary Space: O(n)
We are using a hashmap to store slope points hence the auxiliary space is O(n).
You can also read about the Longest Consecutive Sequence.
Frequently Asked Question
What is an array?
An array is a collection of homogeneous values stored at contiguous memory locations. It is like a staircase, in which each value of placed at every step, and elements can be accessed by knowing the stair number (or index number).
What is Hashing?
Hashing is a technique using which a given value can be transformed into another value. It makes searching more accessible and quicker.
What is an unordered set?
An unordered set is a data structure that is an associative container that holds a collection of singular Key objects. Average constant-time complexity characterizes search, insertion, and removal. Internally, the components are arranged into buckets rather than being sorted in any specific sequence.
Whаt аre the three bаsic operаtions on а hаsh tаble?
There are mainly three basic operations of a hash table.
- Insert − inserts аn element in а hаsh tаble.
- Seаrch − Seаrches аn element in а hаsh tаble.
- Delete − Deletes аn element from а hаsh tаble.
How to find an element in a set?
A built-in method in the C++ STL called set::find returns an iterator to the element that was looked for in the set container. If the element cannot be located, the iterator then moves to the spot immediately following the final element in the set
Conclusion
In this article, we have extensively discussed the problem of Count maximum points on same line.
We hope that this blog has helped you enhance your knowledge of the array data structure and set traversal and if you would like to learn more, check out our articles on
Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc.
Check out this problem - Pair Sum In Array.
Enroll in our courses and refer to the mock test and problems available.
Take a look at the interview experiences and interview bundle for placement preparations.

Do upvote our blog to help other ninjas grow.
Happy Coding!