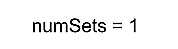Count of Arrangements of RGB balls with No Duplicates in a Set

Vector Approach

This problem is an analysis-based problem, where the given conditions should be considered carefully. First, sort the number of balls in non-decreasing order and then calculate the number of sets with one ball of each color and three balls of the same color. Then, check for the remaining balls and calculate the minimum number of sets required to store them. Finally, return the total number of sets required.

Algorithm

The problem mentioned above can be solved with the following steps:

• Generalize the condition as R <= G <= B by sorting them in order, as the number of sets won’t change with colors.
   
• Calculating sets containing balls of all three colors, which will be the minimum of {R, G, B} i.e., R.  
   
• Now updating Green and Blue balls, by decreasing the number of Red balls from it, G’ = G - R and B’  = B - R.
   
• Now calculate the number of sets containing all three balls of only one color, which will be the sum of G / 3  and B / 3.
   
• Left green balls (G’ = G - R % 3) and blue balls (B’ = B - R % 3) can be covered with the below cases:
  
  
  • G’ and B’ both are zero, so no more sets are required.
     
  • G’ is 0, and B’ is one or two; only one set can accommodate B’ balls.
     
  • G’ and B’ both are one; again, one set will be sufficient.
     
  • In rest all cases, two sets will be required for the left G’ and B’ balls.
     
• Now getting the total of sets calculated in all steps gives the final answer

Dry Run

• First, we create vector balls that contain red, green, and blue balls.
  
  • balls is now {2, 1, 2}.

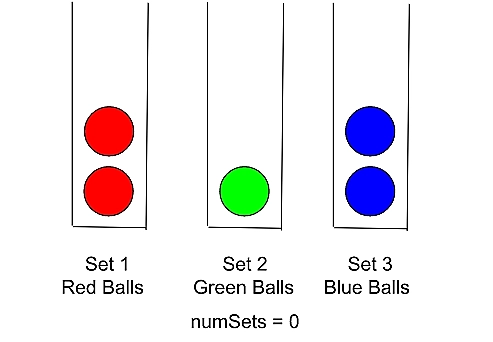
• Next, we sort the balls in non-decreasing order.
  
  • balls is now {1, 2, 2}.

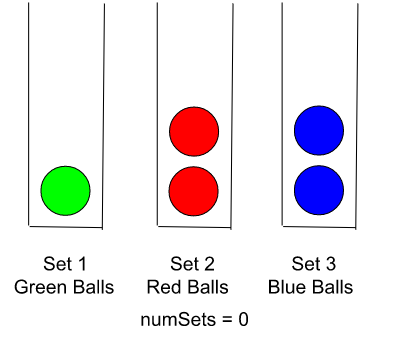
• We then calculate the number of sets with one ball of each color, which is equal to the minimum value in balls.
  
  • numSets is now 1.

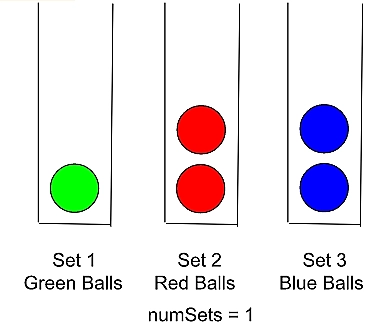
• We then subtract the number of balls used in the first set from the remaining colors, i.e., balls = {1-1, 2-1, 2-1}.
  
  • balls is now {0, 1, 1}.

• We calculate the number of sets with three balls of the same color by dividing the number of remaining balls in each color by 3 i.e., balls = {0%3, 1%3, 1%3}.
  
  • the balls are still {0, 1, 1}.
     
• Since there are no colors with at least 3 balls left, we don't add any sets in this step.

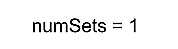
• We then calculate the remaining balls in each color after we have formed all possible sets of three, and one ball of each color.
  
  • balls is still {0, 1, 1}.

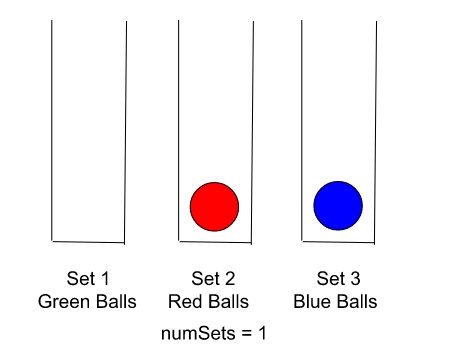
• Finally, we check how many remaining balls we have and add the corresponding number of sets.
   
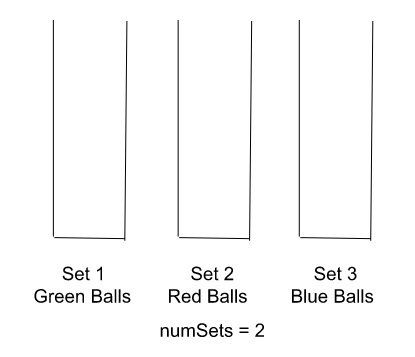
• Since we have one ball left in each of the red and blue colors, we add one set to the total.
   
• Therefore, the function returns 2, which is the minimum number of sets required to form all possible sets of one ball of each color from the given input.

C++ Code

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int calculateMinimumSets(int red, int green, int blue) {
    // Store the number of balls in a vector.
    vector<int> balls {red, green, blue};
    
    // Sort the balls in non-decreasing order.
    sort(balls.begin(), balls.end());
    
    // Number of sets with one ball of each color.
    int numSets = balls[0];  
    balls[1] -= balls[0];
    balls[2] -= balls[0];
    balls[0] = 0;
    
    /*
        Number of sets with three
        balls of the same color.
    */
    numSets += balls[1] / 3;
    numSets += balls[2] / 3;
    
    /*
        remaining number of balls after
        set of three has been formed 
    */
    balls[1] %= 3;
    balls[2] %= 3;
    
    /* 
        No more balls left.
        Nothing happens with numSets.
    */
    if (balls[1] == 0 && balls[2] == 0) {
        numSets;
    } 
    // Two balls left of the same color.
    else if (balls[1] == 1 && balls[2] == 1) {
        numSets++;
    } 
    // Three balls left of different colors.
    else if ((balls[1] == 2 && balls[2] == 0) || (balls[1] == 0 && balls[2] == 2)) {
        numSets++;
    } 
    // Two balls left of different colors.
    else if (balls[1] == 1 || balls[2] == 1) {
        numSets++;
    }
    // More than two balls left of different colors.
    else {
        numSets += 2;
    }
    // Return final numSets
    return numSets;
}

int main() {
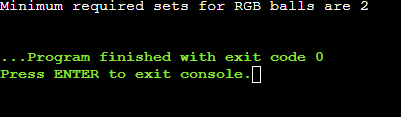
    // Input
    int red = 2;
    int green = 1;
    int blue = 2;
    
    // Call the function and print the result
    int minimumSets = calculateMinimumSets(red, green, blue);
    cout << "Minimum required sets for RGB balls are " << minimumSets << endl;
    return 0;
}

Output

Python Code

def calculateMinimumSets(red, green, blue):
   # Store the number of balls in a list.
   balls = [red, green, blue]
   
   # Sort the balls in non-decreasing order.
   balls.sort()
   
   # Number of sets with one ball of each color.
   numSets = balls[0]  
   balls[1] -= balls[0]
   balls[2] -= balls[0]
   
   # Number of sets with three balls of the same color.
   numSets += balls[1] // 3
   
   numSets += balls[2] // 3
   
   # Remaining number of balls after
   # set of three has been formed 
   balls[1] %= 3
   balls[2] %= 3
   
   # No more balls left.
   if balls[1] == 0 and balls[2] == 0:
       pass
   
   # Two balls left of the same color.
   elif balls[1] == 1 and balls[2] == 1:
       numSets += 1
       
   # Three balls left of different colors.
   elif (balls[1] == 2 and balls[2] == 0) or (balls[1] == 0 and balls[2] == 2):
       numSets += 1
       
   # Two balls left of different colors.
   elif (balls[1] == 1 or balls[2] == 1):
       numSets += 1
       
   # Two balls left of different colors.
   else:
       numSets += 2
   # Return final numSets
   return numSets

# Input
red = 2
green = 1
blue = 2

# Call the function and print the result
minimumSets = calculateMinimumSets(red, green, blue)
print("Minimum required sets for RGB balls are", minimumSets)

Output

Complexity Analysis

Time complexity = O(1)

The time complexity is O(1) since the number of iterations required to compute the result does not depend on input size.
Pushing RGB balls into vector takes O(1) time. Further calculations for the most optimum answer, do not include any loop or function and require only O(1) time.

Space Complexity =  O(1) 

The space complexity is also O(1) because only a fixed number of variables are used to store the information about the balls, and the size of the input does not affect the amount of memory used.

Check out this problem - Duplicate Subtree In Binary Tree

Frequently Asked Questions

What is the purpose of a sort() function in the code?

The sort() function in the code is used to sort the elements in non-decreasing order.

What is the time complexity for the sort() STL function?

The time complexity of the sort() STL function is O(n log n) on average, where n represents the input length.

What is the purpose of the "numSets" variable in the code?

The "numSets" variable is used to keep track of the number of sets required to group the balls.

What data structure is used to store the number of balls in this code?

A vector is used to store the number of balls in this code.

What is the time complexity for accessing an element in a vector by its index?

The time complexity for accessing an element in a vector by its index is O(1).

Conclusion

In this blog, we learned to calculate the minimum required sets to place all the red, green and blue balls. We have implemented the problem in C++ and Python programming languages.

For more similar articles, you can refer following links:

• Catalan Numbers 
• Minimum Number of Arrows to Burst Balloons 
• Chinese Remainder Theorem
   

To learn more about DSA, competitive coding, and many more knowledgeable topics, please look into the guided paths on Coding Ninjas Studio. Also, you can enroll in our courses and check out the mock test and problems available to you. Please check out our interview experiences and interview bundle for placement preparations.

Happy Coding!