
Introduction
Strings are one of the most fundamental data structures that have a wide range of applications. These are also important from the interview point of view. In this article, we will see a very interesting question based on binary strings. We will solve it very intuitively and start with a brute-force approach. Next, we will optimize the solution to reach a better time complexity.
Let’s get started with the problem statement.
Problem Statement
You are given an array arr[] consisting of N binary strings; the task is to count the number of strings that do not contain any Arc Intersection.
First, let’s understand the problem statement.
What is a binary string?
The string, which consists of at most two unique characters, is called a binary string.
E.g., S=”110011” - It has only 0 and 1 as unique characters.
S=”ABBAAB” - Consists of two characters A and B.
While the string S=”ABCAABB” is not a binary string because it has 3 unique characters.
Now, the next term present in the problem statement is Arc Intersection.
What do we mean by arc intersection in a binary string?
In a binary string, if every two consecutive same characters are connected by an arc, then if any two arcs intersect then it implies that there is an arc intersection.
Consider the string S = “110011”.
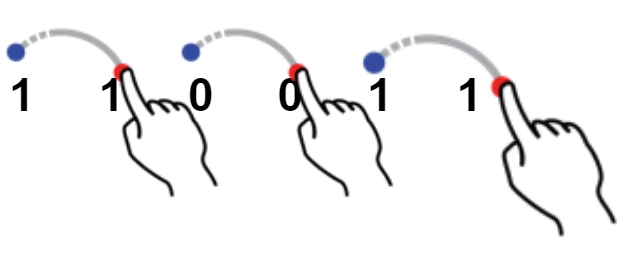
The first 1 is connected to the second 1 by an arc. Then third 0 is joined by an arc with 4th 0. We see that the three arcs do not intersect. So, the given string does not contain arc intersection.
Next, consider another string S=”ABBABAB”.
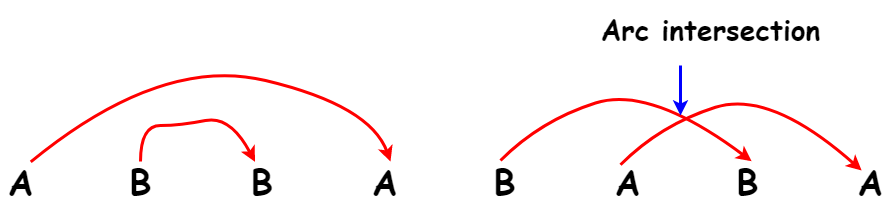
Please try to solve this problem on your own before moving on to further discussion here
We will use a stack to check if there is an arc intersection present in a binary string.
Let’s see the flow of the algorithm -
-
Define a variable count to store the number of desired strings and initialize it with 0.
-
Define a stack which we will use to store the characters of the binary string.
-
Now, iterate through the array of strings and pick a binary string one by one.
-
For a binary string iterate through its characters.
-
Check if the stack is empty. If so, push the current character to the stack. Or If the stack is not empty and the stack top matches with the current character then pop the stack top. Observe that by doing this we get rid of the arc formed by the two characters. In the case when the stack top does not match with the current character, push the current character to the stack.
-
Repeat step 5 for all the characters of the string.
- In the end, check if the stack is empty or not. If it is empty, then the string does not contain arc intersection and increment the count by 1. Else, it has an arc intersection.
Let’s see the code implementation along with the analysis of time and space complexity in the next section.
C++ Implementation
/*C++ code to find the count of strings which does not contain an arc intersection*/
#include <bits/stdc++.h>
using namespace std;
int checkArcIntersection(string S)
{
int len = S.length();
stack<char> stk;
for (int i = 0; i < len; i++)
{
if (stk.empty() || stk.top() != S[i])
{
stk.push(S[i]);
}
else if (!stk.empty() && stk.top() == S[i])
{
stk.pop();
}
}
if (stk.empty())
return 1;
return 0;
}
void cntBinaryStrings(string binaryStrings[], int n)
{
int count = 0;
for (int i = 0; i < n; i++)
{
count += checkArcIntersection(
binaryStrings[i]);
}
cout << "The count of strings which does not contain an arc intersection is: " << count << endl;
}
int main()
{
int n = 4;
string binaryStrings[n] = {"ABBAABAB", "110011", "0101", "AABB"};
cntBinaryStrings(binaryStrings, n);
}
Output
The count of strings which does not contain an arc intersection is: 2Complexity Analysis
Time Complexity
O(n*m), where n is the number of binary strings in the given array and m is the length of the longest string. We have one loop of length n to iterate over all the strings and within that, we call the function checkArcIntersection which iterates over all the characters of the string using a loop of length m. So, this results in two nested loops hence the time complexity is O(n.m).
Space Complexity
In the function checkArcIntersection , we use a stack of length equal to the length of the string. So, if the maximum length of a string is M, then the space complexity will be O(M).





